动态规划之Maximum sum

最新推荐文章于 2022-04-07 17:11:21 发布

原创最新推荐文章于 2022-04-07 17:11:21 发布 · 346 阅读

1 ·

CC 4.0 BY-SA版权

动态规划专栏收录该内容

40 篇文章

订阅专栏

本文介绍了一种最大子段和问题的变种算法实现，通过对数组进行预处理，利用双指针技术减少时间复杂度，避免了二重循环可能导致的超时问题。该算法适用于寻找数组中两个不重叠子段的最大和。

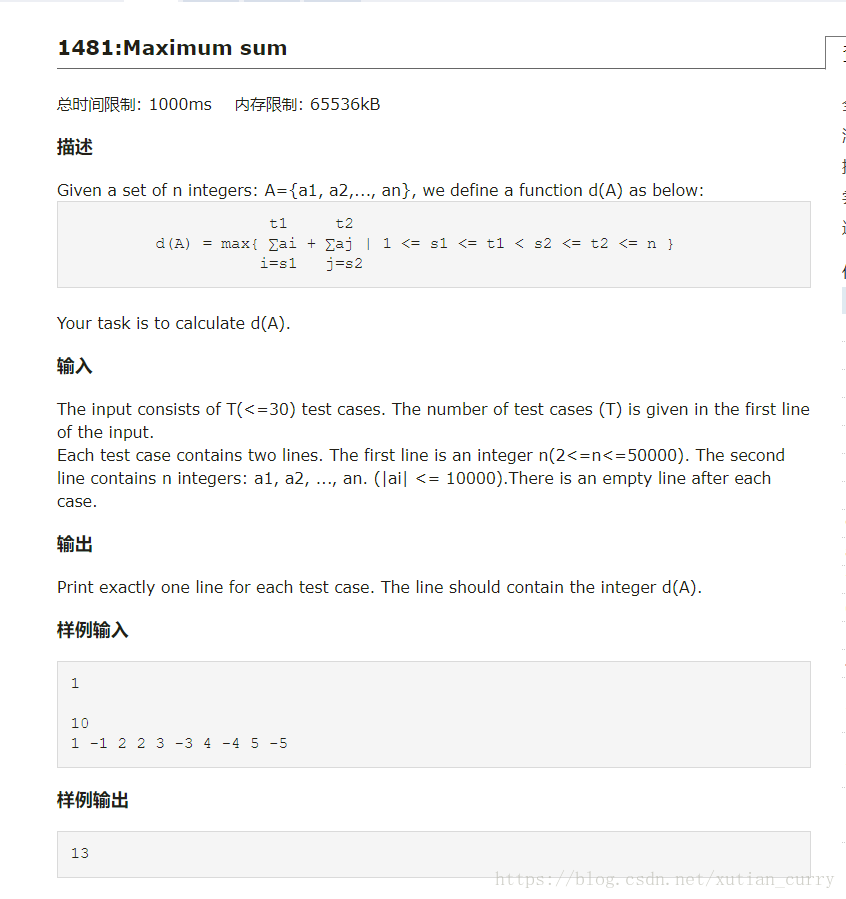
最大子段和的改编版本

需要注意的是初始化

预处理步骤避免二重循环超时

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <string.h>
#include <math.h>
#include <stack>
#include <ctype.h>
using namespace std;
int n;
const int In = (1<<30);
int  a[50005];
int dp1[50005];
int dp2[50005];
int t;
int main()
{
    scanf("%d", &t);
    while( t-- )
    {
        scanf("%d", &n);
        memset(a, 0, sizeof(a));
        memset(dp1, 0, sizeof(dp1));
        memset(dp2, 0, sizeof(dp2));
        for( int i = 1; i <= n; i++ )
        {
            scanf("%d", &a[i]);
            dp1[i] = -(In);
            dp2[i] = -(In);
        }
        for( int j = 1,i = n; j <= n && i >= 1; j++, i-- )
        {
            if( dp1[j-1] > 0 )
                dp1[j] = dp1[j-1] + a[j];
            else
                dp1[j] = a[j];
            if( dp2[i+1] > 0 )
                dp2[i] = dp2[i+1] + a[i];
            else
                dp2[i] = a[i];
        }
        int Max = -(In);
        /**对结果先预处理**/
        for (int j=2; j<=n; j++)
            if (dp1[j]<dp1[j-1]) dp1[j]=dp1[j-1];
        for (int j=n-1; j>0; j--)
            if (dp2[j]<dp2[j+1]) dp2[j]=dp2[j+1];
        for( int i = 1; i < n; i++ )
        {
            Max = max(Max, dp1[i] + dp2[i+1]);
        }
        printf("%d\n", Max);
    }
    return 0;
}