hdu 4565 So Easy!（推公式&矩阵快速幂）

So Easy!

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1029    Accepted Submission(s): 288

Problem Description

　　A sequence S _n is defined as:

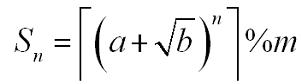
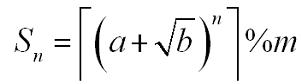
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S _n.
　　You, a top coder, say: So easy!

 

Input

　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2 ¹⁵, (a-1) ²< b < a ², 0 < b, n < 2 ³¹.The input will finish with the end of file.

 

Output

　　For each the case, output an integer S _n.

 

Sample Input

  
  

   
   2 3 1 2013
2 3 2 2013
2 2 1 2013
  
  

 

Sample Output

  
  

   
   4
14
4
  
  

 

Source

2013 ACM-ICPC长沙赛区全国邀请赛——题目重现

 

Recommend

zhoujiaqi2010

 

题意：

a,b,n 都是正整数，求

Sn=⌈(a+b√)n⌉%m,(a−1)2<b<a2

思路：

观察题目b的范围比较有个性。于是深入研究。

把b的范围具体下就得到。

0<( a − b√ )
<1。

得到这个后与题目一联系发现。 ( a + b√ ）与(a−

√b)共轭呀。

也就是说

Cn=An+Bn=(a+b√)n+(a−b√)n

两项共轭，所以 Cn 是整数。

所以sn=cn

Sn=(Cn)%m

求 Cn 的方法是递推。 对 Cn 乘以 (a+b√)+(a−b√)

Cn+1=2aCn−(a2−b)Cn−1

把这个递推式写成矩阵形式

[Cn+1Cn]=[2a1−(a2−b)0][CnCn−1]

于是就可以用矩阵快速幂来做了

[Cn+1Cn]=[2a1−(a2−b)0]n[C1C0]

一个需要注意的地方是快速幂的过程中由于取余可能出现负数，要化为正数。

详细见代码：

#include <iostream>
#include<stdio.h>
using namespace std;
typedef __int64 ll;
ll a,b,n,m;
class tra//矩阵结构
{
public:
    int row,col;//行列
    ll v[3][3];
    tra operator*(tra &tt)//矩阵相乘。前面矩阵的列必须和后面矩阵的行相同
    {
        ll i,j,k;
        tra temp;
        temp.row=row;
        temp.col=tt.col;
        for(i=0; i<row; i++)
            for(j=0; j<tt.col; j++)
            {
                temp.v[i][j]=0;
                for(k=0; k<col; k++)
                {
                    temp.v[i][j]+=v[i][k]*tt.v[k][j];
                    temp.v[i][j]%=m;//由于每次取模。可能把正数变小或变为0。所以最后要特殊处理下
                }
            }
        return temp;
    }
};
tra pow_mod(tra x,ll i)//矩阵快速幂
{
    tra base=x,ans;
    ans.row=ans.col=2;//ans初始化为
    ans.v[0][0]=ans.v[1][1]=1;  //|1  0|
    ans.v[0][1]=ans.v[1][0]=0;  //|0  1|相当于实数里的1
    while(i)
    {
        if(i&1)
            ans=ans*base;
        base=base*base;
        i>>=1;
    }
    return ans;
}
int main()
{
    tra x,ans;

    while(~scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m))
    {
        x.row=x.col=2;
        x.v[0][0]=2*a;
        x.v[0][1]=b-a*a;
        x.v[1][0]=1;
        x.v[1][1]=0;
        x=pow_mod(x,n);
        ans.row=ans.col=1;
        ans.v[0][0]=2*a;
        ans.v[1][0]=2;
        ans=x*ans;
        printf("%I64d\n",(ans.v[1][0]%m+m)%m);//特殊处理。防止变为负数。wa了无数回TT
    }
    return 0;
}
/*
2 1 2 4
2 1 3 3
*/
/*
2
1
*/