多边形裁剪一：Sutherland-Hodgman算法

Sutherland-Hodgman算法

         Sutherland-Hodgman算法也叫逐边裁剪法，该算法是萨瑟兰德(I．E．Sutherland)和霍德曼(Hodgman)在1974年提出的。这种算法采用了分割处理、逐边裁剪的方法。

一，基本思想:

         一次用窗口的一条边裁剪多边形。

        考虑窗口的一条边以及延长线构成的裁剪线该线把平面分成两个部分:可见一侧；不可见一侧。多边形的各条边的两端点S、P。它们与裁剪线的位置关系只有四种

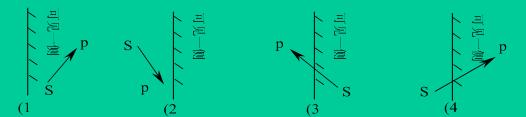
情况（1）仅输出1个顶点P；

情况（2）输出0个顶点；

情况（3）输出线段SP与裁剪线的1个交点I；

情况（4）输出线段SP与裁剪线的1个交点I和1个终点P

二、算法实现：

　　1、已知：多边形顶点数组src，顶点个数n，
　 　　　　　定义新多边形顶点数组dest。

　　2、赋初值：用变量flag来标识：
　　　　　　　　　　0表示在内侧，1表示在外侧。

 3、对多边形的n条边进行处理，对当前点号的考虑为：0～n-1。
　　　for(i=0；i<n；i++)
　　　{
　　　　if(当前第i个顶点是否在边界内侧？)

  {
　　　　　if(flag!=0) /*前一个点在外侧吗？*/
　　　　　{
　　　　　　flag=0；/*从外到内的情况，将标志置0,作为下一次循环的前一点标志*/
　　　　　　(dest + j) =求出交点；　/*将交点dest放入新多边形*/

j++；
}
　　　　　
　　　　　(dest + j)= (src + i)； /*将当前点src_i放入新多边形*/

j++；
}
　　　　else
　　　　{
　　　　　if(flag==0) /*前一个点在内侧吗？*/
　　　　　{
　　　　　　flag=1；/*从内到外的情况，将标志置1,作为下一次循环的前一点标志*/
　　　　　　(dest + j) =求出交点；　/*将交点dest放入新多边形*/

j++；
}
　　　　}
　　　　s= (src + i)； /*将当前点作为下次循环的前一点*/
　　　}

三，算法特点：

　　Sutherland－Hodgeman多边形裁剪算法具有一般性，被裁剪多边形可以是任意凸多边形或凹多边形，裁剪窗口不局限于矩形，可以是任意凸多边形。
　　上面的算法是多边形相对窗口的一条边界进行裁剪的实现，对于窗口的每一条边界依次调用该算法程序，并将前一次裁剪的结果多边形作为下一次裁剪时的被裁剪多边形，即可得到完整的多边形裁剪程序。

[cpp]  view plain copy

1. //点在有向线段那侧  
2. /* 
3. 向量叉积法 
4.  
5.   　　为简单计，测试点表示为P点。假设窗口边界方向为顺时针，如图中所示，对于其中任一边界向量，从向量起点A向终点B看过去： 
6.    
7.     　　如果被测试点P在该边界线右边(即内侧)，AB×AP的方向与X-Y平面垂直并指向屏幕里面，即右手坐标系中Z轴的负方向。 
8.      
9.       　　反过来，如果P在该边界线的左边(即外侧)，这时AB×AP的方向与X-Y平面垂直并指向屏幕外面，即右手坐标系中Z轴的正方向。 
10.        
11.         　　设：点P(x，y)、点A(xA，yA)、点B(xB，yB)， 
12.         　　　　向量AB={(xB-xA)，(yB-yA)}， 
13.         　　　　向量AP={(x-xA)，(y-yA)}， 
14.          
15.           　　那么AB×AP的方向可由下式的符号来确定： 
16.            
17.             V=(xB-xA)·(y-yA)-(x-xA)·(yB-yA) (3-14)  
18.              
19.               　　因此，当V≤0时，P在边界线内侧； 
20.                
21.                 　　　　　而V>0时，P在边界线外侧。 
22.  
23. */  
24. static int _RtInSide(RtVector vector, RtPoint point)  
25. {  
26.     return (vector.ep.x - vector.sp.x) * (point.y - vector.sp.y) - (vector.ep.y - vector.sp.y) * (point.x - vector.sp.x);  
27. }  
28.   
29. //多边形点必须是顺时针方向  
30. int rtPrunePSH(RtPoint* src, int num, RtPoint** dest, int* total)  
31. {  
32.     int i = 0, j = 0, k = -1, flag = 0;  
33.     RtPoint start, stop;//被剪裁多边形  
34.     RtPoint sp, ep;//剪裁窗口  
35.     RtPoint* temp = NULL;  
36.     temp = (RtPoint*)malloc(sizeof(RtPoint) * 3 * (*total));  
37.     if (temp == NULL) return -1;  
38.   
39.       
40.     sp = *(src + num - 1);  
41.   
42.     for ( i = 0; i < num; i++)//剪裁窗口  
43.     {  
44.         ep = *(src + i);  
45.           
46.         start = *((*dest) + *total - 1);  
47.         flag = _RtInSide(rtVector(sp, ep), start) > 0 ? 0 : 1;  
48.   
49.         for ( j = 0; j < *total; j++)//被剪裁的多边形  
50.         {     
51.             stop = *((*dest) + j);  
52.             if (_RtInSide(rtVector(sp, ep), stop) <= 0)//当前第i个顶点是否在边界内侧  
53.             {  
54.                 if (flag == 0)/*前一个点在外侧吗？*/  
55.                 {  
56.                     flag = 1;/*从外到内的情况，将标志置0,作为下一次循环的前一点标志*/  
57.                     k++;  
58.                     CRtPoint<double> point;  
59.                     CRtPoint<int> st(sp.x, sp.y), et(ep.x, ep.y);                   
60.                     CRtLine<int> v1(st, et);  
61.                     st.SetData(start.x, start.y);  
62.                     et.SetData(stop.x, stop.y);  
63.                     CRtLine<int> v2(st, et);  
64.                     v2.Intersect(v1,point);  
65.                     (temp + k)->x = point[0];/*将交点放入新多边形*/   
66.                     (temp + k)->y = point[1];  
67.                 }  
68.                 k++;  
69.                 *(temp + k) =  stop;/*将当前点pi放入新多边形*/   
70.             }  
71.             else  
72.             {  
73.                 if (0 != flag)/*前一个点在内侧吗？*/  
74.                 {  
75.                     flag = 0;/*从内到外的情况，将标志置1,作为下一次循环的前一点标志*/  
76.                     k++;  
77.                     CRtPoint<double> point;  
78.                     CRtPoint<int> st(sp.x, sp.y), et(ep.x, ep.y);                   
79.                     CRtLine<int> v1(st, et);  
80.                     st.SetData(start.x, start.y);  
81.                     et.SetData(stop.x, stop.y);  
82.                     CRtLine<int> v2(st, et);  
83.                     v2.Intersect(v1,point);  
84.                     (temp + k)->x = point[0];/*将交点放入新多边形*/   
85.                     (temp + k)->y = point[1];  
86.                 }  
87.             }  
88.             start = stop;/*将当前点作为下次循环的前一点*/  
89.         }  
90.   
91.         sp = ep;  
92.           
93.         *total = k + 1;  
94.         memcpy(*dest, temp, sizeof(RtPoint) * (*total));  
95.         k = -1;  
96.     }  
97.   
98.   
99.     return 0;  
100. }