关于红黑树（RBT）

最新推荐文章于 2020-10-29 00:18:56 发布
最新推荐文章于 2020-10-29 00:18:56 发布
阅读量331 收藏
点赞数
分类专栏： 学习中的问题
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ybt_c_index/article/details/85217461
版权

本文内容主要是在看完wiki后写的，所以可以直接在wiki中找到关于红黑树的讲解，传送。

这里不罗嗦了，直接开始。

首先，红黑树是一个满足如下属性的二叉查找树（不知道二叉查找树的朋友先去补一下相关知识）：

  1. 每个节点非黑即红。
  2. 根节点为黑。有时可忽略这条规则，因为根节点总是可以由红变黑，但反过来可未必如此，这条规则的影响非常小。
  3. 所有叶子节点（NIL）都为黑。叶子节点无值。
  4. 如果一个节点为红，则它的两个子节点必为黑。
  5. 从一个给定节点到其任一子孙叶子节点（即为NIL的叶子节点，分清内部节点和叶子节点的概念）的所有路径上，所包含的黑色节点数都相同。

以上5条属性就是衡量红黑树的标准，包括插入，删除节点导致的红黑树重新平衡等。

黑色深度表示根节点到一个节点的黑色节点数；黑色高度表示从根节点到叶子节点的所有路径上的统一黑色节点数。

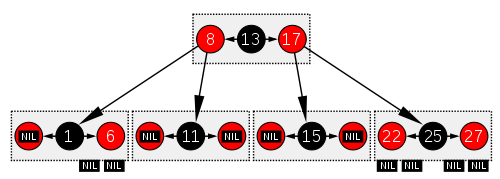
下图就是一个红黑树
来源：wiki

红黑树的结构和order为4的B树相似
在这里插入图片描述

关于后续操作的一些函数方法（C代码）

struct node* parent(struct node* n) {
 return n->parent; // NULL for root node
}

struct node* grandparent(struct node* n) {
 struct node* p = parent(n);
 if (p == NULL)
  return NULL; // No parent means no grandparent
 return parent(p); // NULL if parent is root
}

struct node* sibling(struct node* n) {
 struct node* p = parent(n);
 if (p == NULL)
  return NULL; // No parent means no sibling
 if (n == p->left)
  return p->right;
 else
  return p->left;
}

struct node* uncle(struct node* n) {
 struct node* p = parent(n);
 struct node* g = grandparent(n);
 if (g == NULL)
  return NULL; // No grandparent means no uncle
 return sibling(p);
}

void rotate_left(struct node* n) {
 struct node* nnew = n->right;
 struct node* p = parent(n);
 assert(nnew != LEAF); // since the leaves of a red-black tree are empty, they cannot become internal nodes
 n->right = nnew->left; 
 nnew->left = n;
 n->parent = nnew;
 // handle other child/parent pointers
 if (n->right != NULL)
  n->right->parent = n;
 if (p != NULL) // initially n could be the root
 {
  if (n == p->left)
   p->left = nnew;
  else if (n == p->right) // if (...) is excessive
   p->right = nnew;
 }
 nnew->parent = p;
}

void rotate_right(struct node* n) {
 struct node* nnew = n->left;
 struct node* p = parent(n);
 assert(nnew != LEAF); // since the leaves of a red-black tree are empty, they cannot become internal nodes
 n->left = nnew->right;
 nnew->right = n;
 n->parent = nnew;
 // handle other child/parent pointers
 if (n->left != NULL)
  n->left->parent = n;
 if (p != NULL) // initially n could be the root
 {
  if (n == p->left)
   p->left = nnew;
  else if (n == p->right) // if (...) is excessive
   p->right = nnew;
 }
 nnew->parent = p;
}

基本都是些常规操作（如左旋，右旋等）。

后续的图解中，使用N表示当前操作的节点；P表示N的父节点；G表示N的祖父节点；S表示N的兄弟节点；U表示N的叔伯节点（即P的S节点）。三角形表示不确定深度子树；上面有黑色圆圈的三角形表示其黑色高度比不带的多1.

插入操作

struct node *insert(struct node* root, struct node* n) {
 // insert new node into the current tree
 insert_recurse(root, n);

 // repair the tree in case any of the red-black properties have been violated
 insert_repair_tree(n);

 // find the new root to return
 root = n;
 while (parent(root) != NULL)
  root = parent(root);
 return root;
}

void insert_recurse(struct node* root, struct node* n) {
 // recursively descend the tree until a leaf is found
 if (root != NULL && n->key < root->key) {
  if (root->left != LEAF) {
   insert_recurse(root->left, n);
   return;
  }
  else
   root->left = n;
 } else if (root != NULL) {
  if (root->right != LEAF){
   insert_recurse(root->right, n);
   return;
  }
  else
   root->right = n;
 }

 // insert new node n
 n->parent = root;
 n->left = LEAF;
 n->right = LEAF;
 n->color = RED;
}

insert_recurse方法为递归插入方法，插入节点最后一定是末端节点（有两个NIL叶子节点），和二叉查找树的插入相同；insert_recurse方法为调整插入后的树的方法，使其满足红黑树的条件，同样为递归方法，且最后插入节点的颜色一定是红色（为了满足第五条要求，所有路径的黑色节点数相同，所以插入红色节点时，一定满足该条件）。

接下来讨论插入后会出现的几种情况：

  1. N为根节点。
  2. N的父节点P为黑色。
  3. P为红色（即不是树的根节点），且U（叔伯节点）为红色。
  4. P为红色且U为黑色。
void insert_repair_tree(struct node* n) {
 if (parent(n) == NULL) {
  insert_case1(n);
 } else if (parent(n)->color == BLACK) {
  insert_case2(n);
 } else if (uncle(n)->color == RED) {
  insert_case3(n);
 } else {
  insert_case4(n);
 }
}
  • 要求1（节点非红即黑）和要求3（所有叶子节点为黑）永远满足。
  • 要求2（根节点为黑）在第一种情况中得到满足。
  • 要求4（红色节点只有黑色子节点）只有在插入红色节点时会被破坏，需要将节点由黑变红，或者进行旋转。（这句话可能现在有点难以理解，先往下看）
  • 要求5（所有路径下黑色节点数相同）只有在加入黑色节点时受到破坏，节点需要变色或旋转。（插入节点不是一定是红色吗？为什么会这么说呢？先往下看）
Case 1

N为根节点，直接变色为黑。

void insert_case1(struct node* n)
{
 if (parent(n) == NULL)
  n->color = BLACK;
}
Case 2

P为黑，则要求4（红色节点的子节点都为黑）并没有被破坏。要求5（所有路径黑色节点数都相同）也没有被破坏，因为现在N有两个黑色叶子节点，且N为红色，所以经过N的路径上并没有新增黑色节点数，在N插入前是1，插入后，两个叶子节点还是1.
如下图
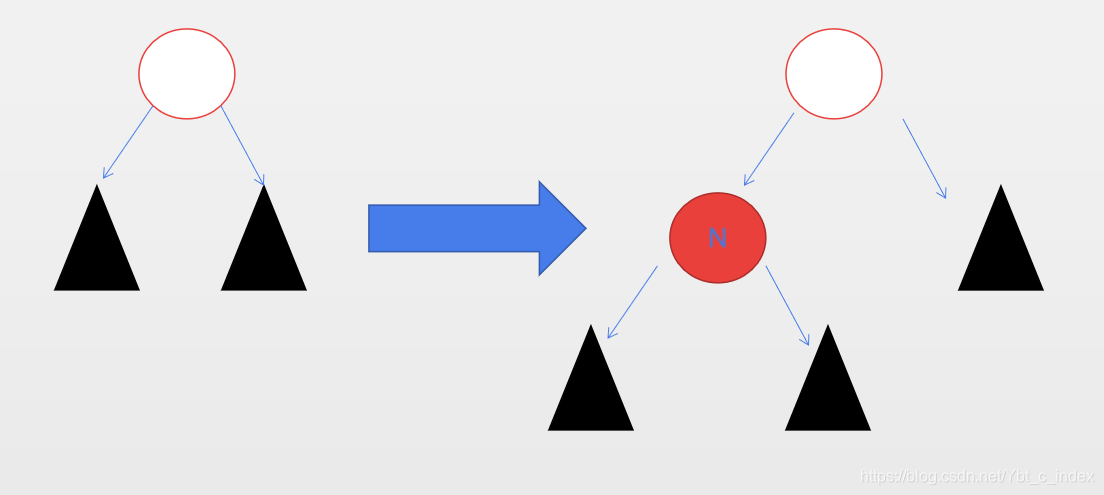
在这里插入图片描述

Case 3

P和U都为红色，则它们都被变为黑色，而G变为红色，这样才能满足要求5。因为经过P或者U的路径必定经过G，经过这样变色后，这些路径的黑色节点数没有发生变化。然而，如果G是根节点时不满足要求2，或者它的父节点为红色时不满足要求4，所以需要让G再执行insert_repair_tree方法。
此种情况图示如下
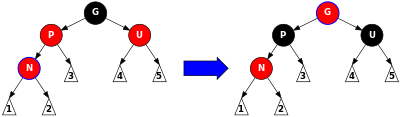
在这里插入图片描述
相关代码如下：

void insert_case3(struct node* n)
{
 parent(n)->color = BLACK;
 uncle(n)->color = BLACK;
 grandparent(n)->color = RED;
 insert_repair_tree(grandparent(n));
}
Case 4

P红，U黑。我们最终的目标是将当前插入的节点N旋转到祖父节点G的位置，但是如果N在G子树的“内侧”时（N为G左子树的右侧子节点或右子树的左侧子节点）无法直接一步旋转。故

第一步
如下图
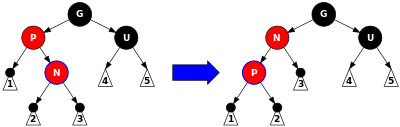
在这里插入图片描述
对P进行左旋（如果N在G的右子树的左侧子结点时，则进行右旋）。旋转后会导致要求4被破坏，但要求5未被破坏。

void insert_case4(struct node* n)
{
 struct node* p = parent(n);
 struct node* g = grandparent(n);

 if (n == g->left->right) {
  rotate_left(p);
  n = n->left;
 } else if (n == g->right->left) {
  rotate_right(p);
  n = n->right; 
 }

 insert_case4step2(n);
}

第二步
当前节点N在G子树的“外侧”（其实就是Case 4的第二种情况，我们上面第一步讨论的是第一种情况）。这种情况下G满足右旋条件，旋转后P为N和G的父节点。由于G为黑色，在不破坏要求4的情况下，P不能再为红色，因此为了满足要求4，P和G的颜色互换。此时要求5依然满足，之前经过节点G的路径现在经过节点P。

注意，如果是从第一步转移到这一步时，当前图示中的N为第一步中的P，P为第一步中的N。

图示如下
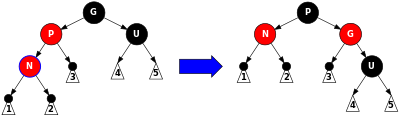
在这里插入图片描述
代码如下

void insert_case4step2(struct node* n)
{
 struct node* p = parent(n);
 struct node* g = grandparent(n);

 if (n == p->left)
  rotate_right(g);
 else
  rotate_left(g);
 p->color = BLACK;
 g->color = RED;
}

到此所有插入情况讨论完毕。在上述算法中，除了Case3会以G节点递归调用Case1，其他情况只会调用一次。由于每次修复树会向上两级，因此插入操作修复树的函数调用次数最大为h/2次。因为升级的概论随着每次迭代呈指数下降，所以平均插入成本实际上是恒定的。

删除操作

在常规二叉查找树的节点（有两个非叶子子节点）删除操作中，我们寻找该节点左子树的最大元素或者右子树的最小元素，并将该元素的值赋给该节点，并删除对应元素的节点，即可完成删除操作。而我们删除的那个元素节点，其必须拥有少于两个非叶子子节点。（在红黑树中，其末端节点必定有两个值为空的黑色子节点）
因为仅仅是复制值不会破坏红黑树的任何要求，所以这就减少了删除那种至多有一个非叶子子节点的节点的问题。一旦我们解决了这个问题，解决方法同样适用删除拥有至少有两个非叶子子节点的节点。

因此，剩下的部分，我们解决了删除最多有一个非叶子项的节点问题。我们用M表示要删除的节点；C将表示M的一个被选定的子节点，我们也称为“its child”。如果M确实有一个非叶子项，则将其称为C；否则，选择其中一个叶子作为其子项C。

如果M为红色节点，我们只需将其替换为它的子项C，因为根据要求4，C必定为黑色。（这仅发生在M有两个叶子节点，如果M有一个非叶子项为黑色，则其替换掉M后会导致要求5被破坏，另一个路径的黑色子节点树+1）。由于通过被删除节点M的路径仅仅是少了一个红色节点，其父节点和子节点都必定是黑色，所以要求3和4不会被破坏。

另一种简单的情况是M为黑色，C为红色。仅是移除黑色节点会破坏要求4和5，但如果我们将C变为黑色，则不会破坏这些规则。

复杂的情况是M和C都为黑色。（这只会发生在删除带有两个叶子项节点时，因为如果节点M有一个黑色非叶子项在一边，但另一边时叶子节点，则路径上的黑色节点数不同，破坏要求5）
我们开始用C替换M（C就是M的其中一个叶子项）。我们将这个C标注为N，它的兄弟节点标注为S。（S为之前的M的兄弟节点）
在下图中，我们用P表示N的新父节点（M的父节点），SL表示S的左子项，SR表示S的右子项。（S不能为叶子节点，因为如果M和C都是黑色，则P的一个包含M的子树拥有两个黑色高度，因此S的子树的黑色高度必须为2，所以S不能为叶子节点）

接下来，我们开始看代码实现。

void replace_node(struct node* n, struct node* child){
    child->parent = n->parent;
    if (n == n->parent->left)
        n->parent->left = child;
    else
        n->parent->right = child;
}

void delete_one_child(struct node* n)
{
 /*
  * Precondition: n has at most one non-leaf child.
  */
 struct node* child = is_leaf(n->right) ? n->left : n->right;

 replace_node(n, child);
 if (n->color == BLACK) {
  if (child->color == RED)
   child->color = BLACK;
  else
   delete_case1(child);
 }
 free(n);
}

replace_node用来将C替换掉M；我们讨论删除delete_one_child的前提是N必须有至少一个非叶子项。

如果N和它的父节点都是黑色，则删除父节点会导致经过N的路径的黑色节点数-1，破坏要求5，因此必须重新平衡。以下是我们需要考虑的几种情况：（以下讨论都是删除节点后进行重新平衡红黑树的算法）

Case 1

N是新的根节点，这种情况下，我们就完成了操作，我们在每个路径上都移除了一个黑色节点，并且新的根节点是黑色的。（这种情况就是，初始红黑树只有一个黑色根节点，然后删除了该根节点，N就是NIL）

void delete_case1(struct node* n)
{
 if (n->parent != NULL)
  delete_case2(n);
}

在case 2，5，6中，我们假定N是P的左子项。

Case 2

S是红色的。这种情况下，我们交换P和S的颜色，然后左旋P，让S成为N的祖父节点。注意P必须是拥有一个红色子项的黑色节点。因为结果子树有一个路径的黑色节点少1（经过N的那个路径，因为之前删除了一个黑色节点）所以我们还没有完成。现在N有一个黑色兄弟节点及一个红色父节点，满足接下来的4，5，6。之后的case中，我们将N的新兄弟节点标识为S。

图示如下
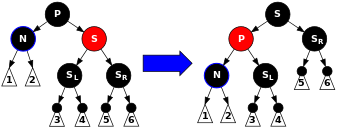
在这里插入图片描述

代码如下：

void delete_case2(struct node* n)
{
 struct node* s = sibling(n);

 if (s->color == RED) {
  n->parent->color = RED;
  s->color = BLACK;
  if (n == n->parent->left)
   rotate_left(n->parent);
  else
   rotate_right(n->parent);
 }
 delete_case3(n);
}
Case 3

P，S及S的子节点都为黑色。这种情况下，我们只需将S变为红色。通过S的所有路径，这些路径之前都不通过N，都少了一个黑色节点。这样，通过P的所有路径的黑色节点数就都相同了，但是都比原来少1，所以需要对P进行重新平衡，进入case1的情况。

图示如下
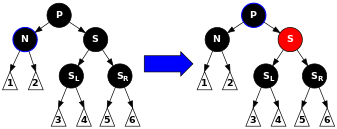
在这里插入图片描述

代码如下：

void delete_case3(struct node* n)
{
 struct node* s = sibling(n);

 if ((n->parent->color == BLACK) &&
     (s->color == BLACK) &&
     (s->left->color == BLACK) &&
     (s->right->color == BLACK)) {
  s->color = RED;
  delete_case1(n->parent);
 } else
  delete_case4(n);
}
Case 4

S和S的子节点都为黑，但P为红。这种情况，我们只需将S和P的颜色交换。这不仅不影响通过S的路径，且通过N路径少1个黑色节点，也因为P的变色给补足回来了。

图示如下
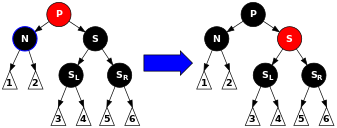
在这里插入图片描述

代码如下：

void delete_case4(struct node* n)
{
 struct node* s = sibling(n);

 if ((n->parent->color == RED) &&
     (s->color == BLACK) &&
     (s->left->color == BLACK) &&
     (s->right->color == BLACK)) {
  s->color = RED;
  n->parent->color = BLACK;
 } else
  delete_case5(n);
}
Case 5

S是黑色，S的右子项为黑色，左子项为红色，并且N是它父节点的左子项。这种情况下，我们对S进行右旋，这样S的左子项成为S的父节点及N的兄弟节点。然后我们交换S和其新父节点的颜色。所有路径仍然拥有相同的黑色节点，但是现在N有一个其右子项为红色的黑色兄弟节点，可以让我们进行case 6。这次转换不会影响N及其父节点。

图示如下
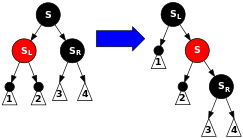
在这里插入图片描述

代码如下：

void delete_case5(struct node* n)
{
 struct node* s = sibling(n);

 if  (s->color == BLACK) { /* this if statement is trivial,
due to case 2 (even though case 2 changed the sibling to a sibling's child,
the sibling's child can't be red, since no red parent can have a red child). */
/* the following statements just force the red to be on the left of the left of the parent,
   or right of the right, so case six will rotate correctly. */
  if ((n == n->parent->left) &&
      (s->right->color == BLACK) &&
      (s->left->color == RED)) { /* this last test is trivial too due to cases 2-4. */
   s->color = RED;
   s->left->color = BLACK;
   rotate_right(s);
  } else if ((n == n->parent->right) &&
             (s->left->color == BLACK) &&
             (s->right->color == RED)) {/* this last test is trivial too due to cases 2-4. */
   s->color = RED;
   s->right->color = BLACK;
   rotate_left(s);
  }
 }
 delete_case6(n);
}
Case 6

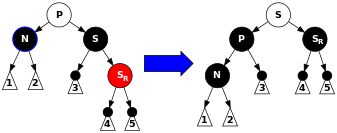
S是黑色的，S的右子项为红色，N是其父节点的左子项。这种情况下，我们对P进行左旋，这样S成为P及S右子项的父节点。之后我们交换P和S的颜色，使S的右子项变为黑色。子树在其根节点还是拥有相同的颜色，所以要求4和5没有被破坏。然而N新增了一个黑色祖先：不论P之前是否为黑色。这样经过N的路径新增了一个黑色节点，弥补了之前被删除的黑色M。

同时，不经过N的路径有两种可能：

  1. 经过N的新兄弟节点SL，它是那个标号为3的子树。它一定经过S和P，不论之前或现在，并且它们仅仅交换了颜色，所以它的路径黑色节点数不受影响。
  2. 经过N的新叔伯节点SR，之前它经过S，S的父节点P，及S的右子项SR，但现在只经过S（颜色和之前的P相同），以及SR（颜色由红变黑），所以最后路径上的黑色节点数同样不受影响。

总之，这些路径上的黑色节点数不受影响。因此我们满足了要求4和5。白色节点的颜色既可以是红，也可以是黑。但必须保证转换前后颜色相同。

图示如下
在这里插入图片描述

代码如下：

void delete_case6(struct node* n)
{
 struct node* s = sibling(n);

 s->color = n->parent->color;
 n->parent->color = BLACK;

 if (n == n->parent->left) {
  s->right->color = BLACK;
  rotate_left(n->parent);
 } else {
  s->left->color = BLACK;
  rotate_right(n->parent);
 }
}

至此，我们讨论完了相关的删除节点的重排情况。上述算法中，除了case3 会递归其父节点到case1。所以case1的循环不会超过h。并且因为升级的概率随着每次迭代呈指数下降，所以平均移除成本是恒定的。

另外，子节点上不会发生尾递归，所以尾递归循环只能从一个孩子移回到它的后继祖先时发生。如果过在case 2中出现旋转（这是在case 1-3的循环内旋转的唯一可能性），之后N的父节点在旋转后变为红色并退出循环。因此，该循环中最多旋转一次。同时在退出循环后最多发生两次额外旋转（case 5，6），所以总计最多发生3次旋转。

一个偏执狂
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
合并两个*.rbt文件
西门吹雪
07-07 764
需求 已有一个rbt文件（A），需要与一个elf(B)文件进行合并 elf文件转换为bin文件，再将bin文件转换为rbt文件 将A和B文件的rbt格式合并 技术要点归纳 elf文件转bin文件，这个需要借助工具exe软件 bin文件的部分数据提取转换为rbt文件 两个文件的合并 使用的小技巧有：内存映射，QtConcurrent，binTHex,cmd 关键代码 内存映射代码 uchar *QFileDevice::map(qint64 offset, qint64 size, QFileDevi
红黑树RBT.cpp
05-07
红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。 [1] 红黑树是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-...
HashMap中红黑树的查找函数find()实现
journey_fan的专栏
04-25 4999
//HashMap中红黑树的查找函数find()实现 /** * 调用树的find()函数 */ final TreeNode getTreeNode(int h, Object k) { return ((parent != null) ? root() : this).find(h, k, null);
RBT(红黑树)的删除算法
xiaoguobaf的博客
08-03 5074
2-3树中删除最小键作为一个热身，回到2-3树来看下删除，简单起见，从删除最小键开始。如果含有最小键的节点不是2节点（3节点或4节点），那么直接删除该节点，不会破坏树的平衡性，但是如果是2节点，由于删除后变为空节点，有可能会破坏平衡性，故删除最小键的思路是沿左链接向下进行变换，确保当前节点不是2节点。 根节点根节点的左右孩子都为2节点此时将3个2节点合并为一个4节点 根节点的右孩子不为2节点左孩
RBT-删除-详细讲解-需要BST删除基础-旋转基础
此战必胜
10-29 489
代码： /* * 作者：流放的未来 * 时间：2020/10/29/8/43 * 红黑树定义： * 1. 根必须为黑。 * 2. 树上节点非红即黑。 * 3. 两个节点不能同时为红色。 * 4. 路径上的黑节点个数一致。 * 5. 所有空节点，默认为黑，俗称黑哨兵。 */ //用到C语言的输入输出等基础函数因此需要 stdio //需要malloc申请地址空间 stdlib #include<stdio.h> #include&l.
RBT(红黑树)插入算法
xiaoguobaf的博客
08-03 1509
#2-3查找树为了保持平衡性，同时也为了避免AVL那样多次的判断和旋转，需要一些灵活性，故允许一个节点可以保存两个键，它有三条链接，称3节点，BST中的节点称2节点。 2-3查找树的定义：它是一棵查找树或空树，由2节点和3节点组成，2节点含有一个键和两条链接，2节点的左子树中的键均小于该节点的键，右子树中的键均大于该节点的键；3节点含有两个键和三条链接，左子树中的键小于该节点的键，中子树中的键在该
RBT.rar_red black tree_红黑树
09-24
运用C++进行红黑树的描述，对红黑树的插入、删除、查找等操作进行了实现等等。
rbt.rar_rbt_red black tree_动态演示_红黑树
09-14
红黑树的实现代码,在VC下可演示红黑树结点的动态变化.
RBT.zip_rbt_搜索树
09-20
红黑树 C代码 算法导论 建立 搜索 插入删除
红黑树_ C++模板实现
11-08
RBTree(node<T> *rbt):root(rbt){}//复制构造函数，用于创建子红黑树对象 void insert(const T&);//插入 void create();//创建红黑树 void erase(const T&);//删除 node* locate(const T&)const;//查找 node* ...
红黑树的例子
08-10
红黑树的一个小例子，可以学习下挺好的，赞一个！
Linux内核红黑树封装的通用红黑树
07-21
通用红黑树 说明： 用Linux内核红黑树封装的一个通用型的红黑树 如何使用该红黑树： 见rbtest1.c和rbtest2.c 直接make生成rbtest1和rbtest2 作者：rcyh 日期：2011年7月21日 ------------------------------------------ Omnipotent Red-black tree comment: Red-black tree the Linux kernel package with a omnipotent red-black tree how to use: see rbtest1.c and rbtest2.c Directly generate rbtest1 and rbtest2 make You can modify and run author: rcyh date: 07/21/2011
通用红黑树（Tree-Map）容器纯C实现
08-05
纯C实现的通用红黑树容器不好找，于是自己琢磨着实现了一个。 算法部分直接剪裁自Linux内核中的rbtree 作者主要是在此基础上封装了一个通用的容器 里面含有 test例子 以及 benchmark基准测试 另外这个是Windows和Linux都可以用的 由于Linux内核的rbtree用了很多C99语法，笔者还得写了一些宏改造内核代码 Linux下的make是完整的 Windows下提供了VS08版的sln文件（只有test木有benchmark） 附带了一个C++里面的STL Map的benchmark
关于登陆的次数限制的简单实现
热门推荐
Ybt_c_index的博客
12-08 1万+
之前被问到一个问题，关于登陆次数限制的问题。比如我每天限制用户只能进行三次错误登陆操作，如果超过三次，那么就锁定账户，一天后才能再次登陆。这个其实也不是很难，不过逻辑还是需要好好验证一下，目前我大概实现成功了，因为测试的次数也有限，所以可能有纰漏，还请各位斧正，不吝赐教。项目结构、 这个项目后来改名了，所以可能名字和GitHub上的不一致，GitHub上项目名是LoginTimes。 还
java实现平衡二叉树
Ybt_c_index的博客
06-08 4847
本文参考海纳的两篇文章，需要补平衡二叉树知识的请看这里。 参照的文章是这篇文章。 可以直接去看这两篇文章，再回头看我这篇文章，所以我就去繁就简。 代码 package com.yubotao; /** * @Auther: yubt * @Description: * @Date: Created in 9:23 2018/6/8 * @Modified By: */ pu...
java实现二叉树的层次遍历
Ybt_c_index的博客
03-20 4167
昨天面试的时候遇到这个问题，由于太久没有接触算法和数据结构了，导致遗忘的比较彻底，当时记得使用队列的特性可以实现层次遍历的问题，但是自己写的时候却没有很好的利用队列的特性，当时的第一想法是递归，最后写着写着就因为找不到好的出口条件，以及各种分支判断，加上如果有兄弟子树，还要写如何处理这种情况等等，最后反正是写不下去了。 所以今天着重记录一下，如何正确的使用队列的特性去实现二叉树的层次遍历。当然这...
2018年中总结（三）工作中遇到的问题（下）
Ybt_c_index的博客
07-05 1212
这部分是另外一家，也就是我目前地公司笔记记录，来这里工作地三个月时间，主要工作是负责调研新技术，目前基本还没接触到业务层面。 最开始是学习spring cloud组件，为公司的服务加上配置中心，这个我之前写过文章，然后尝试加熔断，但是由于涉及代码太多，且Hystrix和代码的耦合度也蛮高的，所以就放弃了。 之后应领导要求，开始熟悉Kubernetes和Istio，应该是为之后做技术储备，但是说...
Go的坑我慢慢填
Ybt_c_index的博客
12-18 919
此篇为记录我学习Go语言遇到的报错，bug等而开设。1.在Linux下使用make命令执行makefile文件时，报错如下： [ERROR] Error getting version: exec: "go": executable file not found in $PATH 然后大概看了意思，就是Linux下的go环境变量的配置有问题，所以刚才写了一篇Linux下Go的环境变量配置的blo
2018年中总结（二）工作中遇到的问题（上）
Ybt_c_index的博客
07-02 758
年初在一家使用golang的公司待了一段时间，当时抱着一颗学习的心态试图挑战一下自己，结果因为自己基础薄弱，能力不足，没能坚持下去，但是却学到了非常多的东西，是一段非常宝贵的工作经历，这里记录一下在工作中遇到的奇奇怪怪的问题，尽量将具体的工作内容剥离出去，记录问题及解决思路和方法等。 1.由于GFW的问题，在国内使用golang是相当困难的，常常需要自备梯子，或者使用公司的vpn，不过这个问题是...
红黑树python实现
最新发布
09-25
红黑树是一种自平衡的二叉搜索树，其在实现上相对复杂。下面是一个红黑树的Python实现的示例代码： ```python # 节点类 class Node: def __init__(self, key): self.key = key self.parent = None self.left = ...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值