模版
void dfs(int x,int y)
{
for(int i=0;i<4;i++)
{
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&g[xx][yy]!='#')
{
g[xx][yy]='#';
dfs(xx,yy);
g[xx][yy]='.';
}
}
}P1683 入门
题目描述
不是任何人都可以进入桃花岛的,黄药师最讨厌像郭靖一样呆头呆脑的人。所以,他在桃花岛的唯一入口处修了一条小路,这条小路全部用正方形瓷砖铺设而成。有的瓷砖可以踩,我们认为是安全的,而有的瓷砖一踩上去就会有喷出要命的毒气,那你就死翘翘了,我们认为是不安全的。你只能从一块安全的瓷砖上走到与他相邻的四块瓷砖中的任何一个上,但它也必须是安全的才行。
由于你是黄蓉的朋友,她事先告诉你哪些砖是安全的、哪些砖是不安全的,并且她会指引你飞到第一块砖上(第一块砖可能在任意安全位置),现在她告诉你进入桃花岛的秘密就是:如果你能走过最多的瓷砖并且没有死,那么桃花岛的大门就会自动打开了,你就可以从当前位置直接飞进大门了。
注意:瓷砖可以重复走过,但不能重复计数。
输入格式
第一行两个正整数 W 和 H,分别表示小路的宽度和长度。
以下 H 行为一个 H×W 的字符矩阵。每一个字符代表一块瓷砖。其中,. 代表安全的砖,# 代表不安全的砖,@ 代表第一块砖。
输出格式
输出一行,只包括一个数,即你从第一块砖开始所能安全走过的最多的砖块个数(包括第一块砖)。
输入输出样例
输入 #1复制
11 9 .#......... .#.#######. .#.#.....#. .#.#.###.#. .#.#..@#.#. .#.#####.#. .#.......#. .#########. ...........
输出 #1复制
59
说明/提示
数据规模与约定
对于全部的测试点,保证 1≤W,H≤20。
#include<bits/stdc++.h>
using namespace std;
int n,m;
char g[30][30];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int sum=0;
void dfs(int x,int y)
{
g[x][y]='#';
sum++;
for(int i=0;i<4;i++)
{
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&g[xx][yy]!='#')
{
dfs(xx,yy);
}
}
}
int main()
{
cin>>m>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>g[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(g[i][j]=='@')
{
dfs(i,j);
}
}
}
cout<<sum;
return 0;
}解法:这道题就是求与@相连的点最多有多少个,所以这道题的深搜可以不用回溯,在开头就把走过的点标记好,每走一步就让步数加加,在主函数里找到@就调用dfs,最后输出sum。
P2802 回家
题目描述
小 H 在一个划分成了 n×m 个方格的长方形封锁线上。 每次他能向上下左右四个方向移动一格(当然小 H 不可以静止不动), 但不能离开封锁线,否则就被打死了。 刚开始时他有满血 6 点,每移动一格他要消耗 1 点血量。一旦小 H 的血量降到 0, 他将死去。 他可以沿路通过拾取鼠标(什么鬼。。。)来补满血量。只要他走到有鼠标的格子,他不需要任何时间即可拾取。格子上的鼠标可以瞬间补满,所以每次经过这个格子都有鼠标。就算到了某个有鼠标的格子才死去, 他也不能通过拾取鼠标补满 HP。 即使在家门口死去, 他也不能算完成任务回到家中。
地图上有五种格子:
0:障碍物。
1:空地, 小 H 可以自由行走。
2:小 H 出发点, 也是一片空地。
3:小 H 的家。
4:有鼠标在上面的空地。
小 H 能否安全回家?如果能, 最短需要多长时间呢?
输入格式
第一行两个整数 n,m, 表示地图的大小为 n×m。
下面 n 行, 每行 m 个数字来描述地图。
输出格式
一行, 若小 H 不能回家, 输出 -1,否则输出他回家所需最短时间。
输入输出样例
输入 #1复制
3 3 2 1 1 1 1 0 1 1 3
输出 #1复制
4
说明/提示
对于所有数据,1≤n,m≤9。
2021.9.2 增添一组 hack 数据 by @囧仙
#include<bits/stdc++.h>
using namespace std;
int n,m;
int g[20][20];
int dp[25][25][10];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int res=100;
void dfs(int x,int y,int sum,int t)
{
if(t>=dp[x][y][sum])
{
return ;
}
dp[x][y][sum]=t;
if(sum==0)
{
return ;
}
if(g[x][y]==3)
{
res=min(res,t);
return ;
}
if(g[x][y]==4)
{
sum=6;
}
for(int i=0;i<4;i++)
{
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&g[xx][yy]!=0)
{
dfs(xx,yy,sum-1,t+1);
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>g[i][j];
}
}
memset(dp,0x3f,sizeof dp);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(g[i][j]==2)
{
g[i][j]=0;
dfs(i,j,6,0);
}
}
}
if(res==100)
{
cout<<-1;
}
else
cout<<res;
return 0;
}解法:这道题的dfs有四个参数,分别是点的行和列、生命值和时间,如果生命值为0就直接退出,如果走到了终点,就让res取个最小值结束,如果碰到鼠标就把sum改为6,循环里调用的时候sum要减1,时间加1,主函数里还要判断如果res还是极大值输出-1,否则输出res。但是这道题用普通的方法会超时,所以要在外面定义一个三维数组,表示走到这个点所需的最小时间,如果现在的时间比他大就直接退出,否则就把这个点的时间修改成现在的时间。
P2080 增进感情
题目背景
小明和小红的感情,是慢慢发展起来的。
题目描述
他们对对方分别有一个好感值。定义两人的亲密程度为两人的好感值之和。
如果他们的亲密程度达到 v,则他们将走到一起。他们以后的生活将取决于两人的好感值之差的绝对值,这个值越小,他们的生活将越幸福。
现在,他们对对方的好感值都为 0,小明有 n 件事可以干,每件事可以增加他对小红的好感 ai 点,并且增加小红对他的好感 bi 点。(可能为负数)
小明可以任选一些事做,请你帮小明求出怎样才能让他们的生活更加幸福(求出两人在一起的前提下,好感值之差的最小绝对值即可)。
输入格式
第一行,两个正整数 n,v。
之后 n 行,每行两个空格隔开的整数 ai,bi。
输出格式
一行,一个非负整数,表示两人在一起的前提下,好感值之差的最小绝对值。如果无论如何两人也无法在一起,输出 -1。
输入输出样例
输入 #1复制
4 15 5 6 -1 8 7 2 1 0
输出 #1复制
3
说明/提示
数据范围与约定
对于 20% 数据,保证 n≤10。
对于 100% 数据,保证 1≤n≤30,1≤∣ai∣,∣bi∣≤100。
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[40],b[40];
int res=1e9;
void dfs(int u,int s1,int s2)
{
if(u>n)
{
if(s1+s2>=m)
{
res=min(res,abs(s1-s2));
}
return ;
}
dfs(u+1,s1,s2);
dfs(u+1,s1+a[u],s2+b[u]);
}
int main()
{
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i]>>b[i];
}
dfs(1,0,0);
if(res==1e9)
cout<<-1;
else
cout<<res;
return 0;
}解法:在dfs里每次调用做和不做两种状态,如果里面的u比n大,里面还要再判断一下如果他们对对方的好感度之和比m大,res就跟他们的差的绝对值取一个最小值,再退出,最后输出res。
P5635 【CSGRound1】天下第一
题目背景
天下第一的 cbw 以主席的身份在 8102 年统治全宇宙后,开始了自己休闲的生活,并邀请自己的好友每天都来和他做游戏。由于 cbw 想要显出自己平易近人,所以 zhouwc 虽然是一个蒟蒻,也有能和 cbw 玩游戏的机会。
题目描述
游戏是这样的:
给定两个数 x,y,与一个模数 p。
cbw 拥有数 x,zhouwc 拥有数 y。
第一个回合:x←(x+y)modp。
第二个回合:y←(x+y)modp。
第三个回合:x←(x+y)modp。
第四个回合:y←(x+y)modp。
以此类推....
如果 x 先到 0,则 cbw 胜利。如果 y 先到 0,则 zhouwc 胜利。如果 x,y 都不能到 0,则为平局。
cbw 为了捍卫自己主席的尊严,想要提前知道游戏的结果,并且可以趁机动点手脚,所以他希望你来告诉他结果。
输入格式
有多组数据。
第一行:T 和 p 表示一共有 T 组数据且模数都为 p。
以下 T 行,每行两个数 x,y。
输出格式
共 T 行
1 表示 cbw 获胜,2 表示 zhouwc 获胜,error 表示平局。
输入输出样例
输入 #1复制
1 10 1 3
输出 #1复制
error
输入 #2复制
1 10 4 5
输出 #2复制
1
说明/提示
1≤T≤200。
1≤x,y,p≤10000。
#include<bits/stdc++.h>
using namespace std;
int t,p;
short vis[10010][10010];
int dfs(int op,int x,int y)
{
if(op==0)
{
if(vis[x][y]!=-1)
{
return vis[x][y];
}
vis[x][y]=0;
if(x==0)
{
return vis[x][y]=1;
}
if(y==0)
{
return vis[x][y]=2;
}
int a=x,b=y;
if(op==0)
{
x=(x+y)%p;
}
else
{
y=(x+y)%p;
}
return vis[a][b]=dfs(!op,x,y);
}
else
{
if(x==0)
{
return 1;
}
if(y==0)
{
return 2;
}
int a=x,b=y;
if(op==0)
{
x=(x+y)%p;
}
else
{
y=(x+y)%p;
}
return dfs(!op,x,y);
}
}
int main()
{
ios::sync_with_stdio(0);
cin>>t>>p;
memset(vis,-1,sizeof vis);
for(int i=1;i<=t;i++)
{
int x,y;
cin>>x>>y;
if(dfs(0,x,y))
cout<<dfs(0,x,y)<<"\n";
else cout<<"error\n";
}
return 0;
}解法:dfs要有三个参数,一个表示轮到谁,剩下两个表示题中的x和y,思路都挺简单的,但是op=0的时候要用记忆化,所以还要判断一下。
P2919 [USACO08NOV] Guarding the Farm S
题目描述
农场有许多小山丘,约翰农夫希望在这些小山丘上放置守卫,以确保他珍贵的奶牛的安全。
他想知道如果他希望在每个小山丘的顶部放置一个守卫,他需要多少守卫。他有一张地图,这张地图是一个整数矩阵;矩阵有 N 行(1<N≤700)和 M 列(1<M≤700)。矩阵中的每个元素表示一个高度 Hij(0≤Hij≤10,000)。请帮助他确定地图上有多少个山顶。
一个山顶是由一个或多个相邻且具有相同值的矩阵元素组成,这些元素被地图的边缘或具有较低(较小)高度的元素完全包围。如果两个不同的元素的 X 坐标差的绝对值不大于 1,且 Y 坐标差的绝对值也不大于 1,则它们是相邻的。
输入格式
* 第 1 行:两个用空格分隔的整数:N 和 M
* 第 2 行到第 N+1 行:第 i+1 行描述矩阵的第 i 行,包含 M 个用空格分隔的整数:Hij
输出格式
* 第 1 行:一个整数,表示山顶的数量
显示翻译
题意翻译
输入输出样例
输入 #1复制
8 7 4 3 2 2 1 0 1 3 3 3 2 1 0 1 2 2 2 2 1 0 0 2 1 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 1 1 1 0 0 1 2 2 1 1 0 0 1 1 1 2 1 0
输出 #1复制
3
说明/提示
有三个山峰:左上角高度为 4 的一个,底部高度为 2 的一个点,以及右上角高度为 1 的一个点。 (由 ChatGPT 4o 翻译)
#include<bits/stdc++.h>
using namespace std;
int n,m;
int g[710][710];
int vis[710][710];
int dx[8]={0,0,1,-1,1,1,-1,-1};
int dy[8]={1,-1,0,0,1,-1,1,-1};
struct node
{
int h,a,b;
}p[1000010];
int cmp(node x,node y)
{
return x.h>y.h;
}
void dfs(int x,int y)
{
for(int i=0;i<8;i++)
{
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&g[xx][yy]<=g[x][y]&&vis[xx][yy]==0)
{
vis[xx][yy]=1;
dfs(xx,yy);
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin>>n>>m;
int idx=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>g[i][j];
p[++idx]={g[i][j],i,j};
}
}
sort(p+1,p+1+idx,cmp);
int cnt=0;
for(int i=1;i<=idx;i++)
{
if(vis[p[i].a][p[i].b]==0)
{
// cout<<p[i].a<<' '<<p[i].b<<endl;
vis[p[i].a][p[i].b]=1;
dfs(p[i].a,p[i].b);
cnt++;
}
}
cout<<cnt;
return 0;
}解法:这次标记需要额外定义一个数组,还要判断周围是否都比他大,其余都一样这次还要用结构体排序,每调用dfs计数器加加,输出cnt。
P1790 矩形分割
题目描述
有一个长为 a,宽为 b 的矩形(1≤a≤6,2≤b≤6)。可以把这个矩形看作是 a×b 个小方格。
我们现在接到了这样的一个任务:请你计算出,把这个矩形分割成两个部分的方法总数。
你不是可以任意地分割这个大的矩形,必须满足:
分割后,每个部分,至少各自均有一个方格是在大矩形的最外边上(即大矩形最外面一环的方格)。
输入格式
输入文件仅包含两个数字,a 和 b。
输出格式
输出仅有一行一个整数,表示分割的方案总数。
输入输出样例
输入 #1复制
3 2
输出 #1复制
15
说明/提示
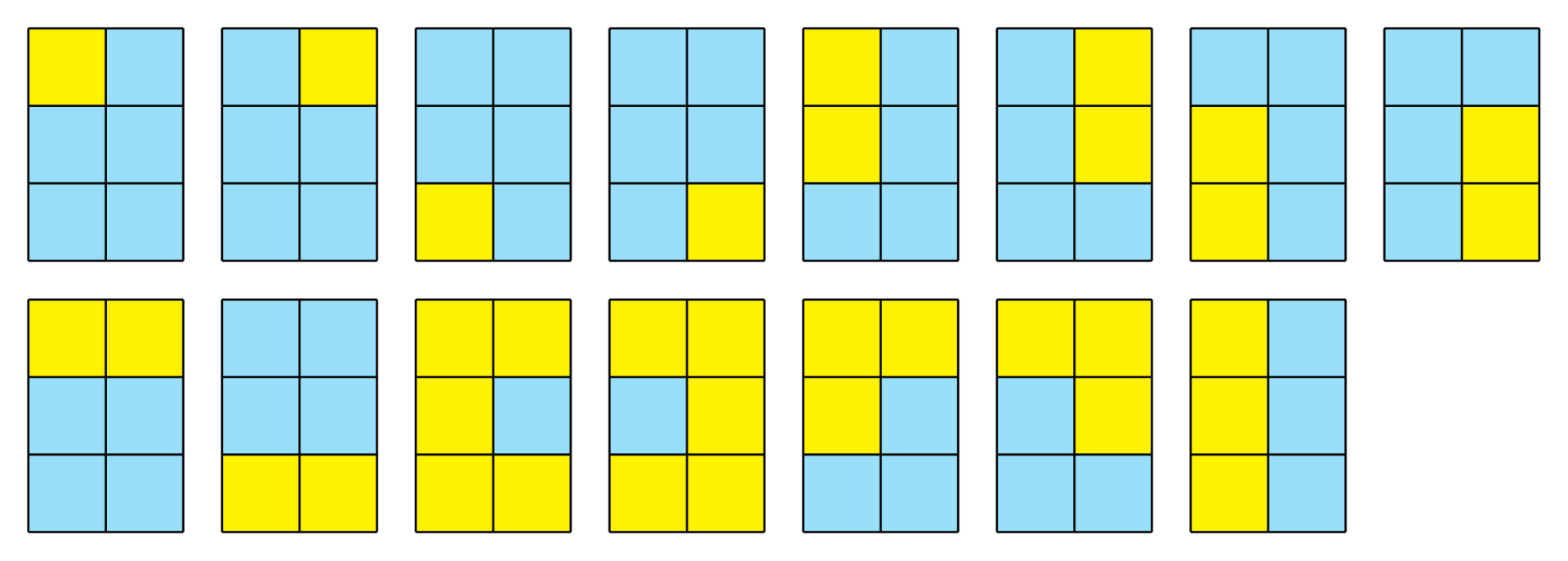
#include<bits/stdc++.h>
using namespace std;
int n,m;
int vis[10][10];
int dx[8]={0,0,1,-1,1,1,-1,-1};
int dy[8]={1,-1,0,0,1,-1,1,-1};
int sum=0;
void dfs(int x,int y)
{
if(x==1||x==n||y==1||y==m)
{
sum++;
return ;
}
for(int i=0;i<4;i++)
{
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&vis[xx][yy]==0)
{
vis[xx][yy]=1;
dfs(xx,yy);
vis[xx][yy]=0;
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin>>n>>m;
n++;
m++;
for(int i=2;i<m;i++)
{
vis[1][i]=1;
vis[2][i]=1;
dfs(2,i);
vis[2][i]=0;
vis[1][i]=0;
}
for(int i=2;i<n;i++)
{
vis[i][1]=1;
vis[i][2]=1;
dfs(i,2);
vis[i][2]=0;
vis[i][1]=0;
}
cout<<sum;
return 0;
}解法:这次也是要额外定义数组来标记,要回溯,dfs里判断如果碰到边界方法数加加,退出,最后输出sum。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








