(浮点数精度问题)CF - 614A_1e18浮点数-CSDN博客

本文探讨了在给定范围内寻找所有K的幂次方的有效算法。通过对比不同数据类型如longlong、double、longdouble及int128的使用，分析了它们的精度和适用场景，提供了一种快速解决问题的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：

给定三个数l,r,k，按从小到大的顺序输出在[l,r]内的所有的k的幂次方.

题解：

直接从k的0次方开始暴力枚举，直到找到最后一个小于等于r的数停止枚举.

在最坏的情况下，k=2，l=1 , r=1e18，只有60个结果，不用担心TLE.

法1：

直接使用long long，但是long long的最大值是9223372036854775807，所以当暴力枚举到最后一个小于等于r的数的时候可能出现再乘一次k直接爆long long的情况，这个时候需要再这里特判一下，如果r除以mi小于k的时候，就说名mi乘上k结果大于r而不是等于r们直接结束枚举.

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
const int maxn=4e4+100;
const int maxm=4205;
ll l,r,k,mi;
int main()
{
    cin>>l>>r>>k;
    bool flag=false;
    mi=1;
    int mid=0;
    while(mi<=r)
    {
        if(mi>=l)
        {
            cout<<mi<<" ";
            flag=true;
        }
        if(r/mi<k) break;
        mi*=k;
    }
    if(!flag)
    {
        cout<<"-1";
    }
    return 0;
}

法2：

这种方法可分成很多小方法：

①：long double（厉xuan害xue）

使用float的时候wa3:

18102 43332383920 28554
输出结果：28554 815330944

正确结果：28554 815330916

Input
18102 43332383920 28554
Output
28554 815330944 
Answer
28554 815330916 

使用double的时候wa34

Input

1 999999999999999999 1000000000

Output

1 1000000000 1000000000000000000

Answer

1 1000000000

很显然，使用float和double的时候对于本题来说爆精度了.

上图转载自：传送门（侵删）

value of floating-point = significand x base ^ exponent , with sign

so,对于float和double来说，其指数范围分别是-127~128和-1023~1024,float的范围为-2^128 ~ +2^128，近似等于-3.40e+38 ~ +3.40e+38，double的范围为-2^1024 ~ +2^1024，近似等于-1.79e+308 ~ +1.79e+308。

下面是对double的一个测试：

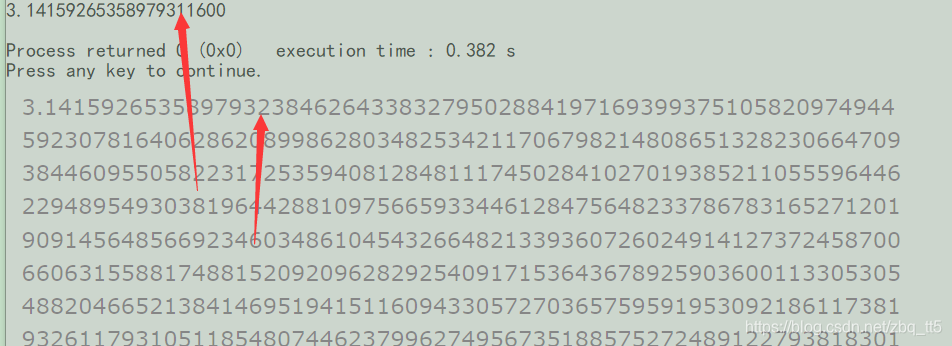
可以看到，在我这里精度应该是16位

下面是对long double的一个测试：

#include<cstdio>
#include<cmath>
using namespace std;
int main()
{
    long double a;
    a=(long double)acos(-1);
    printf("%.20Lf\n",a);
    return 0;
}

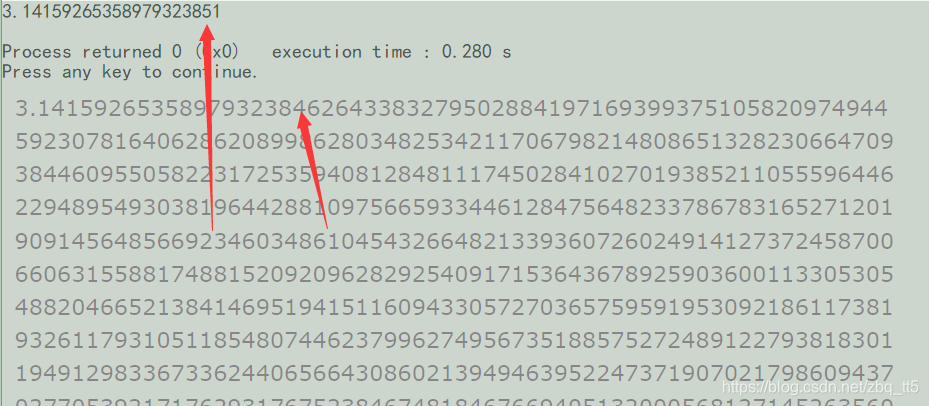
按照我的电脑，精度为18位，

这道题用long double可以水过，不过需要注意的是输出的时候用%.0Lf(xuanxue)

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<vector>
#include<cstring>
#include<queue>
#include<set>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

long double l,r,k,mi;
long double mi;
int main()
{
    cin>>l>>r>>k;
    bool flag=false;
    mi=1;
    while(mi<=r)
    {
        if(mi>=l)
        {
            printf("%0.Lf ",mi);
            flag=true;
        }
        mi*=k;
    }
    if(!flag)
    {
        cout<<"-1\n";
    }
    else{
        cout<<endl;
    }
    return 0;
}

②：int 128

如果不进行特判，使用int128是相对来说比较精准而且比较简单的方法.

不过int128只能在Linux操作系统上运行，windows上打开编译器应该直接报错.

不过很多题的OS是Linux

所以即便是在Windows下不能运行，有时候还是能AC的.

注意：使用C++的cin和cout不能输入输出int 128，需要手写一个输入输出外挂.

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<vector>
#include<cstring>
#include<queue>
#include<set>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;
inline __int128 read(){
    __int128 x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

inline void print(__int128 x){
    if(x<0){
        putchar('-');
        x=-x;
    }
    if(x>9)
        print(x/10);
    putchar(x%10+'0');
}

__int128 mi,l,r,k;
int main()
{
    l=read(),r=read(),k=read();
    bool flag=false;
    mi=1;
    while(mi<=r)
    {
        if(mi>=l)
        {
            print(mi);
            cout<<" ";
            flag=true;
        }
        mi*=k;
    }
    if(!flag)
    {
        cout<<"-1\n";
    }
    else{
        cout<<endl;
    }
    return 0;
}

还有很多可以解决这题的方法....用最快的时间解决才是王道.如果数据范围超级大，直接搞一个大数乘法模板就行了.

但直接使用python等支持大数的语言会更好....