《编程之美》1.4 买书问题 贪心法则

在书中，作者分析两种解法

解法一是贪心，最后得到的结论是：贪心不成立

解法二是dp ， 也类似于递归，最后是成立的

在这里我们重点分析贪心法不成立的原因，以及如何改进

贪心法的适用有两个必要条件，即优化子结构和贪心选择性。优化子结构是成立的，在书中的解法二已经证明了。

对于贪心选择性：最基本的理解就是，每次选择当前最优的步骤，到最后就能得到整个问题的最优解法。我个人认为这只是贪心最基本的解释。

其实很多问题或者是算法都不是一成不变的，有时候，算法或思想是这样的，但我们可以在基本思想不变的情况下，根据题目进行一些改进或者是加入一些符合题目的条件（情况）。

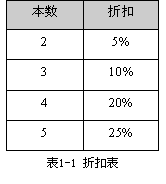
对于买书这个折扣如下：     

                                   

我们来看几个例子：

1、 2   2    2    1    1

这个例子我们可以这样分解：  1  1   1   1   1   +   1  1  1   0   0和 1  1   1  1  0 +  1  1  1  0  1

通过折扣的计算，我们可以得到这个的（1  1   1  1  0 +  1  1  1  0  1） 折扣更大。

2、2   2    1   1    0

这个例子我们可以这样分解：  1  1   1   1   0   +   1  1  0   0   0和 1  1   1  0  0 +  1  1  0  1  0

通过折扣的计算，我们可以得到这个的（1  1   1  1  0 +  1  1  0  0  0） 折扣更大。

3、2   1   1  0   0

这个例子我们可以这样分解：  1  1   1   0   0   +   1  0  0   0   0和 1  1   0  0  0 +  1  0  1  0  0

通过折扣的计算，我们可以得到这个的（1  1   1  0  0 +  1  0  0  0  0） 折扣更大。

有上面3个例子我们可以得到，就只有第一个例子不符合我们的贪心思想。

那我们是否能这样，其他情况我们都用贪心来解决，而第3个例子这种情况，我们就特殊处理

下面是我的代码：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

int num[5];
int ze[5]; //保存每种折扣有多少个
double kou[4] = { 0.25, 0.2 , 0.1 , 0.05}; 

int main()
{
    while(1)
    {

    int i , max_sum = 0 , j;
    for(i = 0; i < 5; i++)
    {
        cin>>num[i];
        max_sum += num[i];
        ze[i] = 0;
    }

    
    double sum = 0;

    i = 0;
    for(i = 0; i < 5; i++) //i = 0 表示买5本 i = 1 表示买 4本 
    {
        sort(num , num+5);//重小到大的排序
        if(num[i] == 0)  continue; 
        if(i == 2) //这就是特殊情况
            //对于特殊情况，我们是把它和 买5本情况 ， 重新组合，变成 买两个 4本
        {
            int x = min(num[i] , ze[0]);
            ze[0] -= x;
            ze[i-1] += 2*x;
            ze[i] = num[i]-x;
            for(j = i+1; j < 5; j++)
                num[j] -= num[i];
            num[i] = 0;

        }
        else
        {
            ze[i] = num[i];
            for(j = i+1; j < 5; j++)
                num[j] -= num[i];
            num[i] = 0;
        }
    }

    sum = max_sum*8.0;

    for(i = 0; i < 4; i++)
    {
        sum -= (5-i)*ze[i]*8*kou[i];
    }

    cout<<sum<<endl;
}
    return 0;
}

通过和书中第二个解法 ， 进行的数据测试对比我们得到 ， 这种变形的贪心解法是正确的。

具体的分析为什么是正确的 ： 点击打开链接