遍历-算法的万能钥匙

图结构：非常强大的结构化思维（或数学）模型。如果您能用图的处理方式来规范化某个问题，即使这个问题本身看上去并不像个图问题，也能使您离解决问题更进一步。

在众多图算法中，我们常会用到一种非常实用的思维模型--遍历（traversal）:对图中所有节点的探索及访问操作。

两种著名的基本遍历策略：

深度优先搜索（depth-first search）

广度优先搜索（breadth-first search）

==================================================================================

如果一个图中的任何一个节点都有一条路径可以到达其他各个节点，那么它就是连通的。

连通分量：目标图中最大（且独立）的连通子图。

找出这种连通分量的方法之一就是：从图中的某个部分开始，逐步扩大其连通子图的确认范围，直至它再也无法向外连通为止。

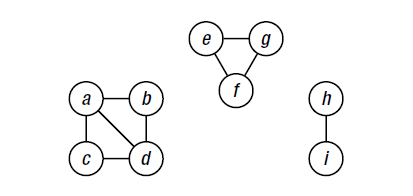
清单5-1：遍历一个表示为邻接集的图结构的连通分量

def walk(G,s,S=set()):
    P,Q=dict(),set()
    P[s]=None
    Q.add(s)
    while Q:
        u=Q.pop()
        for v in G[u].difference(P,S):
            Q.add(v)
            P[v]=u
    return P

if __name__=="__main__":
    a, b, c, d, e, f, g, h, i= range(9)
    N = [
        {b, c, d}, # a
        {a, d}, # b
        {a,d}, # c
        {a,c,d}, # d
        {g,f}, # e
        {e,g}, # f
        {e,f}, # g
        {i}, # h
        {h} #i
    ]
    P=walk(N,a,S=set())

运行结果:

初始化时
P: {0: None}
Q: {0}
u:  0
for循环中：
v: 1
P: {0: None, 1: 0}
Q: {1}
for循环中：
v: 2
P: {0: None, 1: 0, 2: 0}
Q: {1, 2}
for循环中：
v: 3
P: {0: None, 1: 0, 2: 0, 3: 0}
Q: {1, 2, 3}
u:  1
u:  2
u:  3

从第一个连通分量中的a入手，找到了与a相连的点b,c,d。然后再也无法向外连通。P就是最终找到的连通分量。

字典对象P的主要作用是表示已经访问过的前驱节点，每当我们往队列中添加新的节点时，都会同时设置其前驱节点。

将这些前驱节点组合在一起，就形成了相应的遍历树。

然而，该walk函数所遍历的只是单个连通分量（既定目标是个无向图）如果想要找出该图的所有的连通分量，我们就要将其封装在一个涉及所有节点的循环中。

清单5-2 找出图中的连通分量

def components(G):
    comp=[]
    seen=set()
    for u in range(9):
        print("循环中u:",u)
        if u in seen:continue
        C=walk(G,u)
        seen.update(C)
        comp.append(C)
        print("comp:",comp)
        print("seen:",seen)
        
    return comp

if __name__=="__main__":
    a, b, c, d, e, f, g, h, i= range(9)
    N = [
        {b, c, d}, # a
        {a, d}, # b
        {a,d}, # c
        {a,c,d}, # d
        {g,f}, # e
        {e,g}, # f
        {e,f}, # g
        {i}, # h
        {h} #i
    ]
##    P=walk(N,b,S=set())

    comp=components(N)

运行结果：

循环中u: 0
comp: [{0: None, 1: 0, 2: 0, 3: 0}]
seen: {0, 1, 2, 3}
循环中u: 1
循环中u: 2
循环中u: 3
循环中u: 4
comp: [{0: None, 1: 0, 2: 0, 3: 0}, {4: None, 5: 4, 6: 4}]
seen: {0, 1, 2, 3, 4, 5, 6}
循环中u: 5
循环中u: 6
循环中u: 7
comp: [{0: None, 1: 0, 2: 0, 3: 0}, {4: None, 5: 4, 6: 4}, {7: None, 8: 7}]
seen: {0, 1, 2, 3, 4, 5, 6, 7, 8}
循环中u: 8

walk函数返回的是一个已被访问的前驱节点的映射集（递归树），而我们将这些映射集收进了comp列表中（以代表连通分量）。另外，我们还用seen集合来确保自己不会遍历到之前连通分量中的节点。seen.update(C)是一个有关C的规模的线性操作，我们调用walk的工作量也基本是相同的。

总而言之，找出图中的连通分量应该是一个O（E+V）时间的操作，因为该图中的各条边和节点都是必须探索的。