《机器人动力学与控制》第九章——动力学
9.4 欧拉-拉格朗日方程法应用举例(上)
本节我们用前面学到的欧拉-拉格朗日方程分析法来分析四种不同结构的机械臂,并尝试着推导对应的动力学方程。这些例子由简入深,我们先从一个双连杆机械臂开始,最后到一个具有五个连杆的机械臂。这里建议大家自己跟着过程推一波公式,虽然不一定能让你对动力学有更深层次的理解(步骤都是死的),但起码可以通过推导2轴机器人去感受6轴机器人动力学公式的恐怖。
9.4.1. 双连杆笛卡尔机械臂
考虑下图具有两个连杆和两个移动关节的机械臂:
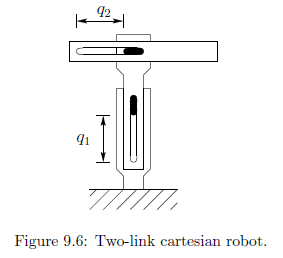
分别用
m
1
m_1
m1 和
m
2
m_2
m2 来表示连杆1和连杆2的质量,用
q
1
q_1
q1 和
q
2
q_2
q2 来表示两个关节的位移量,用
f
1
f_1
f1 和
f
2
f_2
f2 来表示作用在每个关节的力。因为没有转动关节,因此我们不需要考虑转动动能与转动势能。
动能
由于
q
1
q_1
q1 和
q
2
q_2
q2 可以用来表达这个系统的generalized coordinate(这句话直译,具体含义没搞懂),动能可以用如下公式表达:
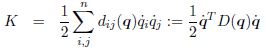
势能仅仅与q1和q2有关,我们用9.3节学到的公式来推导动力学方程。两个关节只有位移没有旋转,所以角速度Jacobian系数为零,该系统的动能只与移动关节的位移速度有关。
通过雅各比矩阵的学习可知连杆1重心的速度等于:
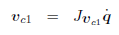
其中
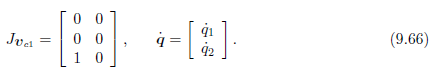
这里省略了建立坐标系,推导雅各比矩阵的过程,请自行推导。类似地,可以得到:
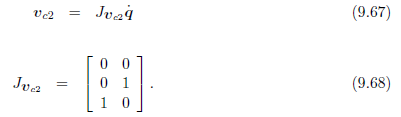
因此该系统的全部动能可以表达为
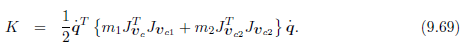
势能
下面就需要推导势能了,根据机器人的结构可以发现,m1和m2的势能都只与q1有关,很容易就能得到该结构的总势能
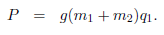
书写动力学方程
有了动能和势能就可以通过写动力学方程了。这里有两种方法,一个是根据定义先写出拉格朗日系数
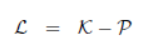
然后使用力的计算公式
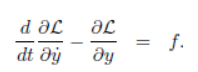
第二种方式是用上一节我们刚刚学习的结论,直接套用公式
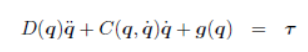
可以发现 D(q) 已知,由于dij与q无关,因此Christoffel项都是0。另外D的非对角项都为0,所以动力学公式变为
由于
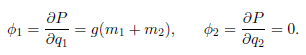
所以最终动力学公式为
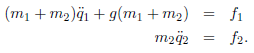
9.4.2.平面肘部机械手
现在我们来看另一个例子,如下图所示,该机器人有且仅有两个旋转关节。
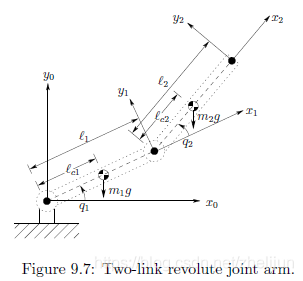
坐标系都已经在图里面帮你们建好了,请自行验证。Ii代表连杆i关于一根过其质心指向朝外的轴的惯量矩。
我们继续使用雅各比矩阵的知识求解速度先,雅各比矩阵推导规则如下
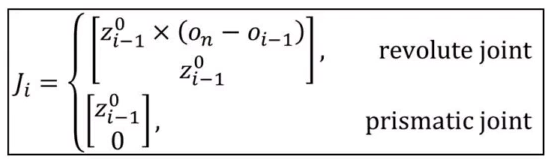
首先
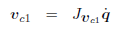
接着
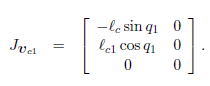
同理
因此动能里面平动部分的能量为
现在我们来处理转动部分能量,根据该机械结构可以方便的得到
根据雅各布矩阵得到的也是一样的结果
接着带入动能表达式得到
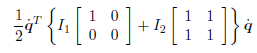
把平动部分能量和转动部分能量相加得到
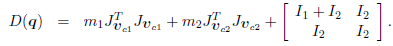
因此
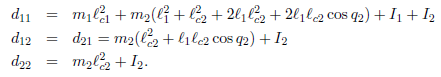
接着
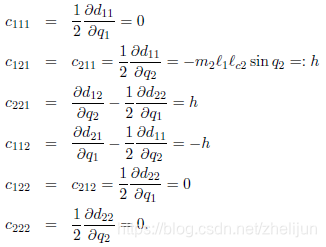
注意,这里面的计算还是比较烦的,我这边省略了不少中间过程直接把结果贴出来。
接下来研究机械臂的势能,势能只与q的大小有关,因此
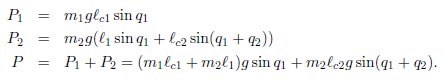
所以
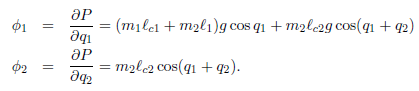
最后我们带入动力学方程得到
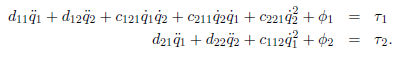
这里面的C项为
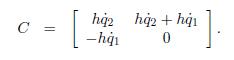
请务必自己推一波,多准备点纸。
参考文献
《robot dynamics and control》 作者:Mark W Spong,Seth Hutchinson, and M. Vidyasagar








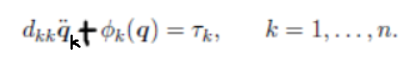













 2848
2848











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








