leetcode：300. 最长递增子序列

题目来源

• leetcode：300. longest-increasing-subsequence 最长递增子序列
• lintcode：76 · Longest Increasing Subsequence · 最长上升子序列

题目描述

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {

    }
};

题目解析

题意：

• 需要对「子序列」和「子串」这两个概念进行区分；
  • 子序列（subsequence）：子序列并不要求连续，例如：序列 [4, 6, 5] 是 [1, 2, 4, 3, 7, 6, 5] 的一个子序列；
  • 子串（substring、subarray）：子串一定是原始字符串的连续子串
• 题目中的「上升」的意思是「严格上升」。反例： [1, 2, 2, 3] 不能算作「上升子序列」；
• 子序列中元素的相对顺序很重要，子序列中的元素必须保持在原始数组中的相对顺序。如果把这个限制去掉，将原始数组去重以后，元素的个数即为所求；

大概意思可以这么理解：从给定数组从挑选若干数字，这些数字满足：如果i < j 则num[i] < nums[j]。问：一次可以选择最多满足条件的数字是多少个。

蜘蛛纸牌

这道题目来源于普林斯顿Patience Sort。

游戏规则

对于n张扑克牌。

1. 不能将大牌放到小牌上
2. 可以新建一个新牌堆，并在上面放一张牌

游戏目标

使得n张牌组成的牌堆数最少

贪心做法

放置一张牌，查看是否有可以放置的牌堆(牌堆顶的牌大于这张牌)。

• 如果有，放在满足条件的最左边的牌堆上面(lefyMost)
• 如果没有，自己成为一个新牌堆。

为什么每次放到leftMost牌堆？

假设目前有两个牌堆，顶部牌分别是[8, 10]。这时打算放置7和9

1. 7放到leftMost，两个牌堆顶变为[7,10]，然后放9，牌堆顶变为[7,9]，最终有两个牌堆
2. 7不放到leftMost，两个牌堆顶变为[8,7]，然后放9，没有合适的牌堆所以自己成为新牌堆，牌堆顶变为[8,7,9]，最终有三个牌堆

因此，每次放到leftMost可以保证最终牌堆数最少

LIS

规律1

• 在任意状态下，所有牌堆的顶部数字，一定是递增的，因此贪心的过程中可以用二分查找当前牌要放入的牌堆

规律2

• 任一递增子序列(IS)的长度，一定小于等于最少的牌堆数，因为每个牌堆从上到下是递减的，要构成IS，每个牌堆最多取一张牌（考虑牌的初始顺序）
  因此，LIS长度=最少牌堆数

LIS算法

1. 使用piles数组保存牌堆的顶部数字，size记录牌堆数
2. 遍历所有牌，对于当前牌x，二分查找前面是否有合适的牌堆，如果有，x覆盖leftMost牌堆的顶部数字；如果没有，新建牌堆，piles数组追加元素x，size++
3. 返回size

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> piles;
        int size=0;
        for(int x:nums){
            //二分查找leftMost
            int left=0,right=size-1;
            while(left<=right){
                int mid=left+(right-left)/2;
                if(piles[mid]>=x){
                    right=mid-1;
                }else{
                    left=mid+1;
                }                
            }
            
            if(left==size){//没有满足条件的pile
                piles.push_back(x);
                size++;
            }
            else{
                piles[left]=x;
            }
        }
        return size;
    }
};

思路二（本质和上面是一样的）

暴力

假设有$[10,9,2,5,3,7,101,4,1]$

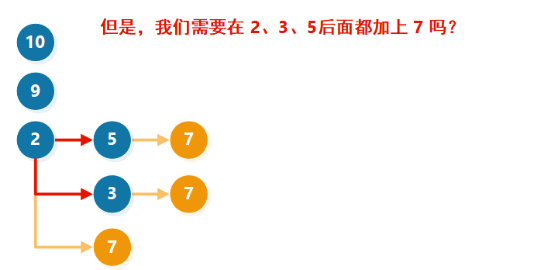
优化

$[10,9,2,5,3,7,101,4,1]$

我们来看插入了所有数组元素后形成的图（子序列要保持相对顺序，所以只能往后插）：

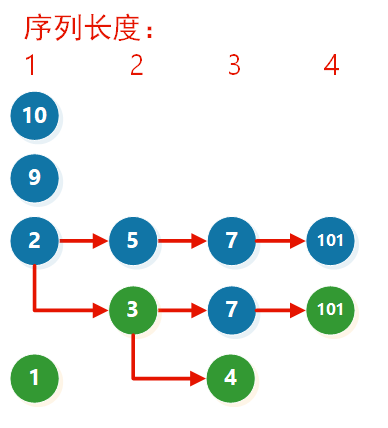
假如我们要在里面新增一个元素X，希望找出插入X之后的最长子序列，则从贪心的角度考虑（尽可能增加子序列的长度），我我们需要在当前允许插入的最长子序列之后添加元素。于是，我们可以依次检查序列长度 =1,2,3,4递增子序列，然后找出最长的，尾数 <X的序列

我们发现，对每一个序列长度 l，只需要检查图中的每一列的最小值（绿色的元素）是否 <X 即可。如果绿色的元素 <X，表明长度为 l的递增子序列后可添加元素 X。

因此，我们只需要维护长度为l的递增子序列的最小结尾数字。这就是官方题解中为什么要把$dp[i]$定义成长度为$i$的递增子序列的最小尾数(下标从1开始)的原因。在本例中，$d=[1,3,4,10]$，注意，$[1,3,4,101]$不是任何一个实际存在于数组的递增子序列

此外，d数组一定是严格递增的。因为$d[i]$（下标从1开始）为长度为$i$的递增子序列末尾的最小数字，而长度为i+1的递增子序列一定是长度为i的递增子序列添加长度而来，如果长度为i的递增子序列的[最小尾数]为X，那么添加的元素一定 > X

实现

最简单的实现方式，当插入新元素X时，我们从逐个枚举现有递增子序列的长度，直到找到最大可添加元素X的长度。与此同时，维护每个长度l的最小尾数。

比如前述序列 [10, 9, 2, 5, 3, 7, 101, 4, 1]，已构造 d数组 [1, 3, 4, 101]，要添加 6。

• 长度l = 1时，长度为1的递增子序列末尾的最小数字为1，6>1，可以添加
• 长度l = 2时，长度为2的递增子序列末尾的最小数字为3，6>3，可以添加
• 长度l = 3时，长度为3的递增子序列末尾的最小数字为4，6>4，可以添加
• 长度l = 4时，长度为3的递增子序列末尾的最小数字为101，101>6，不可以添加。
• 因此，以6为结尾的递增子序列最长为3+1=6
• 另外，此时，长度为4的递增子序列的最小尾数变成了6。因此修改101->6。数组变为[1, 3, 4, 6]

如果要添加 “102”呢？

• 由于 “102” > “101”，因此 “102” 可以在长度为 4 的子序列后添加，递增子序列的最大长度变成了 55。
• 由于长度为 5的递增子序列的尾数只有 “102”，故最小尾数也是 “102”，直接在数组后添加 “102”即可。

优化：

• 由于数组是有序的，当要添加数x时，可以用二分搜索找出数组中小于x的最小数字，以及对应的下标i
• 另外，如果$d[i]<x$，则$d[i+1]>=x$。因此需要将$d[i+1]$修改为$x$，代表长度为$i+1$的递增子序列末尾的最小数字（下标从 1 开始）。

实现：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        //用来存储预期的结果
        std::vector<int> piles;
        piles.push_back(nums[0]);
        for (int i = 1; i < nums.size(); ++i) {
            //如果nums[i]比arr的最大值还大，可以组成一个更长的子序列
            //并将其添加到arr末尾
            if(piles.back() < nums[i] ){
                piles.push_back(nums[i]);
                continue;
            }

            //如果nums[i]比arr最大值小，就要在arr中找查找一个合适的位置，
            //将nums[i]放入，这查找过程是二分查找
            auto pos = lower_bound(piles.begin(), piles.end(), nums[i]) - piles.begin();
            piles[pos] = nums[i];
        }

        return piles.size();
    }
};

具体过程可以参见动画

思路三

暴力穷举

所有的穷举都可以写成递归

假设有$[10,9,2,5,3,7,101,18]$

我们以10为例，看看以10开头的最长上升子序列是什么。

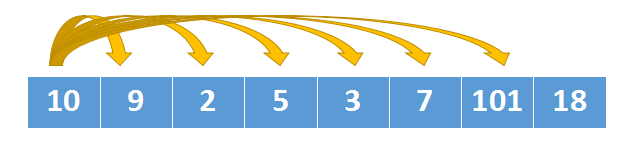
在上图中，我们依次做如下操作：

1. 9比10小，不满足上升条件，继续往后查找
2. 2比10小，不满足上升条件，继续往后查找
3. 5比10小，不满足上升条件，继续往后查找
4. 3比10小，不满足上升条件，继续往后查找
5. 7比10小，不满足上升条件，继续往后查找
6. 101比10大，满足上升条件，子序列长度 + 1

[10. 101]就是一个上升子序列，由于101后面的18比它小，就没法组队了。

以10开头的最长上升子序列就是[10，101]，当然[10，18]也是。

从上图我们可以知道，从$nums[i]$为起点，一路找下去直到$nums[max]$，如果i < j 则num[i] < nums[j]，那么[nums[i],nums[j]]就是一个上升子序列。

按照同样的方式：

• 处理9和后面的元素，就能找到以9开头，最长的子序列。
• 处理2和后面的元素，就能找到以2开头，最长的子序列。

但这种思路也不完全对，比如[2,5]是一个上升子序列，[2,3]也是一个上升子序列。但是选择[2,3]肯定比[2,5]更好。

为什么呢？因为3比5小，[2,3]组队的话，如果后面能碰到一个4，或者5，那么组到一起就是[2,3,4]长度是3，而[2,5]后面就不能再跟上4了，[2,5]后面除非碰到比5大的，否则长度只能是2了。

当i < j，并且nums[i] < nums[j]时，此时有两种选择：

• 将nums[i]和nums[j]组成一个子序列，子序列长度+1
• nums[i]放弃nums[j]，看后面还有没有更好的数字可以组合

对于递归函数来说，就可以这么实现了:

• 如果nums[i]>=nums[j]，放弃nums[j]，继续比较后面的元素
• 如果nums[i]<nums[j]，将这两个元素组成一个子序列
• 如果nums[i]<nums[j]，放弃nums[j]继续比较后面的元素

再看下递归函数的执行过程，以[1,2,3,4,5]举例，执行这个数组的递归调用树部分如下:

图中的根节点是f(-1,0)，第一个参数是上一个元素的下标位置，第二个参数是当前元素的下标位置，f是函数名。

比如f(0,1)表示下标为0的元素跟下标为1的元素比较，因为满足匹配条件，所以有两条路可以走:

• 匹配，子序列长度+1，继续比较下标1和下标2的元素，对应图中的f(1,2)
• 放弃，子序列长度不变，继续比较下标0和下标2的元素，对应图中的f(0,2)

如果是f(11,22)就表示数组下标11的值跟数组下标22的之比较，如果满足上升条件，同样也有两个选择，将f(11,22)+1，然后继续判断f(22,23)，或者判断f(11,23)

class Solution {
    int dfs(int pre, int cur, vector<int>& nums){
        if(cur == nums.size()){
            return 0;
        }

        int a = 0;
        int b = 0;

        //pre小于0是初始状态，继续往后判断
        // if条件满足说明是上升子序列，长度要+1
        if(pre < 0 || nums[pre] < nums[cur]){  // 前序
            a = dfs(cur, cur + 1, nums) + 1;
        }

        //如果不满足可能是不满足上升子序列条件
        //也可能是 满足条件但主动放弃
        b = dfs(pre,cur+1,nums);

        

        return std::max(a, b);
    }
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        return dfs(-1, 0, nums);
    }
};

备忘录算法

我们在函数的入口处判断一下相关的参数是否在缓存中，如果在直接返回就可以了，这样后面就省去一大堆重复计算。如果不在缓存中，则需要新计算一遍，再将结果放入缓存中。

class Solution {
    int dfs(vector<std::vector<int>> &cache, int pre, int cur, vector<int>& nums){
        if(cur == nums.size()){
            return 0;
        }

        if(cache[pre + 1][cur] > -1){
            return cache[pre + 1][cur];
        }

        int a = 0;
        int b = 0;



        //pre小于0是初始状态，继续往后判断
        // if条件满足说明是上升子序列，长度要+1
        if(pre < 0 || nums[pre] < nums[cur]){  // 前序
            a = dfs(cache, cur, cur + 1, nums) + 1;
        }



        //如果不满足可能是不满足上升子序列条件
        //也可能是 满足条件但主动放弃
        b = dfs(cache, pre,cur+1,nums);



        return  cache[pre+1][cur] = std::max(a, b);
    }
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return -1;
        }

        //因为pre是从-1开始的，所以二维数组的行数需要+1
        vector<std::vector<int>> cache(
                nums.size() + 1,
                std::vector<int>(nums.size(), -1));

        return dfs(cache, -1, 0, nums);
    }
};

递归+记忆化的时间复杂度理论上和动态规划是差不多的，但实际执行中时间复杂度上还有常数级别的差异，递归调用本身就需要多耗费一点时间

动态规划

（1）准备

下图中上半部分是递归执行的过程，下半部分是动态规划的执行过程。

• 递归的执行过程，10跟9，2，5，3，7，101依次比较
• 动态规划的执行过程，以101为起点，依次跟前面的元素比较，这个过程刚刚跟递归相反

为什么要反着执行呢？是因为后面的结果需要依赖前面的结果。

（2）具体分析

• 首先数组下面那一排数字并不是下标，而是多态规划计算出来的临时结果
• 10，9，2 这三个元素都递减的，所以到2为止，最长的上升子序列长度为1(因为找不到其他数字可以组队了，最长子序列就是这个数字本身)。
• 而5比2大，所以到5为止，上升子序列长度为2，这个2是怎么来的呢，他是根据前面计算出的来结果再推算出来的。
• 同理，到7为止上升子序列长度为3，这个3是根据5下面的那个2推算出来
• 到101为止，上升子序列长度为4，这个4是根据7下面的那个3推算出来的

于是我们可以得出下面的结论。

• 假设$nums[\mathrm{0...}j]$这段的最长上升子序列长度为$n$，如果$i>j$，并且$nums[i]>nums[j]$，那么$nums[\mathrm{0...}j]$这段的最长上升子序列长度为$n+1$
• 从而：

$$dp[i]=max(dp[i],dp[j]+1)；0<=j<i而且nums[j]<nums[i]$$

数组下面那一排是动态规划计算时用到的数组(以下简称DP数组)，它的长度跟元素数组长度一样，所以空间复杂度就是O(N)了，从这里也可以看到动态规划就是用空间换时间。

DP数组初始的时候元素全部置于1

• 当遍历到元素5的时候，因为5的下标大于2，而且5>2，那么5对应的dp数组就是：dp[3]=max(dp[3],dp[2]+1)
• 3的下标大于2的下标，且3>2，所以dp[4]=max(dp[4],dp[2]+1)
• 7的下标大于5的下标，且7>5，所以dp[5]=max(dp[5],dp[3]+1)
• 101的下标大于7的下标，且101>7，所以dp[6]=max(dp[6],dp[5]+1)

由于每轮都需要迭代i次，总的时间复杂度就是O(N^2)，同时我们会发现，DP数组中最后一个值并非是最终结果。最长的上升子序列长度可能会出现在DP数组中的任意位置，所以我们还需要求一下max(dp)找出最大值再返回就可以了。

class Solution {


public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        //用来存储预期的结果
        std::vector<int> dp(nums.size(), 1);

        for (int i = 0; i < nums.size(); ++i) {  // 遍历i
            for (int j = 0; j < i; ++j) {  // 对于每个nums[i], 都跟i前面的数比较(因为dp[i]的状态跟前面所有数有关)
                if( nums[j] < nums[i]){  // 形成了一个递增序列
                    dp[i] = std::max(dp[i], dp[j]  + 1); //那么更新dp[i]
                }
            }
        }

        //返回dp数组中的最大值
        return *std::max_element(dp.begin(), dp.end());
    }
};

递归写法：

class Solution {

    //函数test表示前面n个元素的最长递增子序列的值
    int test(vector<int>& nums,vector<int>& result,int n){

        //记忆化搜索结果存在，出口result[0] = 1包含在内
        if(result[n]) return result[n];

        int res = 0;
        for(int i = 0; i < n; ++i){
            if(nums[i] < nums[n])
                res = max(res,test(nums,result,i));
        }

        result[n] = res + 1;
        return result[n];
    }

    // 10, 9, 2, 5, 3, 7, 101, 4, 1



public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        //用来存储预期的结果
        std::vector<int> result(nums.size(), 0);
        result[0] = 1;

        //从头到尾挨个搜索
        for(int i = 0; i < nums.size(); ++i){
            test(nums,result,i);
        }

        //求数组中的最大值
        auto maxPosition = max_element(result.begin(), result.end());
        return *maxPosition;
    }
};

贪心 + 二分查找

我们之前说过，同样是长度为2的子序列，[2,3]就比[2,5]好。
因为[2,3]后面如果有4的话，组成[2,3,4]长度就是3了，但是[2,5]因为不满足条件，就没法组队了。

我们组成子序列的时候，不仅要让这个序列尽可能的长，而且要让子序列中的上升的时候尽可能的缓慢，[2, 3]就比[2, 5]上升的缓慢，这样就有机会拼出更长的上升子序列。

我们用一个数组来保存当前的最长上升子序列，这个数组是严格递增的。

因为是严格递增的，数组中最后一个值$nums[max]$就是最大值，如果下次再碰到一个数字n，它比$num[max]$还要大，那么很明显，这个子序列的长度就要+1，并且将数组n添加到数组的末尾。

假设我们正在遍历数组，已经得到的最长上升子序列如下：

$[2,3,7,8,11,13,18]$是目前为止最长的上升子序列，之后如果又碰到了19，或者101，因为他们都大于数组中的最大值18，所以直接将其添加到数组末尾就可以了，同时子序列的长度要+1。

19和101的例子很好理解，但如果下次碰到的数字是6或者12呢？

因为要让子序列上升的尽可能缓慢，那么让$[2,5,\mathrm{7...}]$变成$[2,5,\mathrm{6...}]$更合适，因为后者上升的更缓慢。

同样,将$[...8,11,13,18]$变成$[...8,11,12,18]$也是上升的更缓慢一点。

也就是，已知$[i,i_1,i_2,....,i_n]$，现在我们在继续遍历的过程中碰到了一个值$i_k$，这个值是小于$i_n$的，所以上升子序列的长度还是不变。但是我们需要找到一个位置，将$i_k$替换掉某个旧的值。

这个替换的方式，用的是二分查找，但跟普通的二分查找稍稍不同，这个查找过程描述如下：给定一个排序数组和一个目标值，在数组中找到目标值，并将其替换。如果目标值不存在于数组中，找到它将会被按顺序插入的位置i，将其插入位置i。

最长上升子序列的执行过程如下，绿色部分是最长上升子序列数组

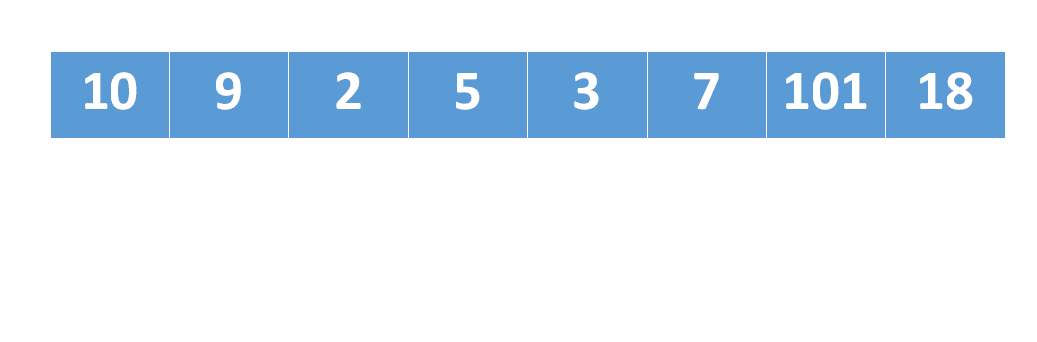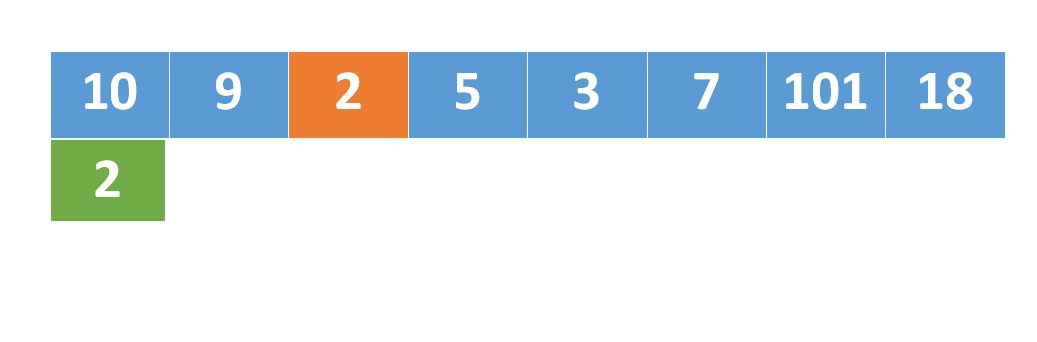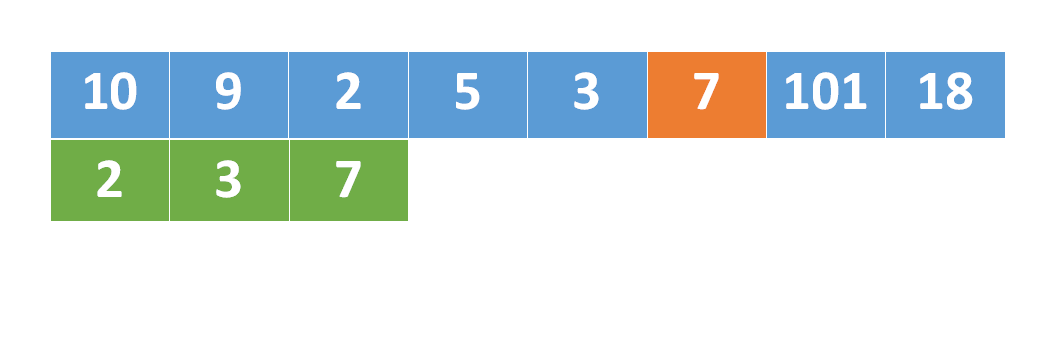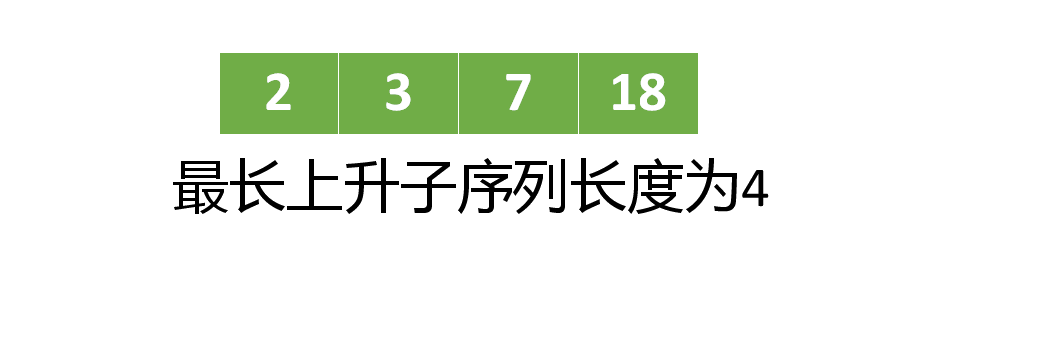
class Solution {


public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        //用来存储预期的结果
        std::vector<int> vec;
        vec.push_back(nums[0]);
        for (int i = 1; i < nums.size(); ++i) {
            //如果nums[i]比arr的最大值还大，可以组成一个更长的子序列
            //并将其添加到arr末尾
            if(vec.back() < nums[i] ){
                vec.push_back(nums[i]);
                continue;
            }

            //如果nums[i]比arr最大值小，就要在arr中找查找一个合适的位置，
            //将nums[i]放入，这查找过程是二分查找
            auto pos = lower_bound(vec.begin(), vec.end(), nums[i]) - vec.begin();
            vec[pos] = nums[i];
        }

        return vec.size();
    }
};

动态规划小结

• dp[n]表示前n个元素的最长递增子序列的长度（最后一个数依赖前n-1个元素，即最后的状态依赖于前面所有的状态）
  • 由于每个数都能独立成为一个子序列，因此起始必然有$f[i]=i$
  • 枚举区间$[0,i)$的所有数$nums[j]$，如果满足$nums[j]<nums[i]$，说明$nums[i]$可以接在$nums[i]$结尾的后面形成上升子序列，此时使用$f[j]$更新f[i]，即有$f[i]=f[i]+1$

递归写法：

class Solution {

    //函数test表示前面n个元素的最长递增子序列的值
    int test(vector<int>& nums,vector<int>& result,int n){

        //记忆化搜索结果存在，出口result[0] = 1包含在内
        if(result[n]) return result[n];

        int res = 0;
        for(int i = 0; i < n; ++i){
            if(nums[i] < nums[n])
                res = max(res,test(nums,result,i));
        }

        result[n] = res + 1;
        return result[n];
    }

    // 10, 9, 2, 5, 3, 7, 101, 4, 1



public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        //用来存储预期的结果
        std::vector<int> result(nums.size(), 0);
        result[0] = 1;

        //从头到尾挨个搜索
        for(int i = 0; i < nums.size(); ++i){
            test(nums,result,i);
        }

        //求数组中的最大值
        auto maxPosition = max_element(result.begin(), result.end());
        return *maxPosition;
    }
};

暴力

假如我们现在要处理的数组为：[0,1,0,3,2,3]，那么会产生的情况会是以下路径：

• 如图可见，我们的结果会在不确定的地方进行分叉。
• 分叉的时候我们需要它继承上阶段的结果。在他结束的时候收回他的结果，并和result进行比较。
• 最后返回的就是最大的结果。
• 但我们从路径可以看出，它产生了太多类似的路径，这会最终导致我们超时。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }

        int result = 1;

        std::function<int(int j, int res)> getNum  = [&](int j, int res)->int {
            int base = nums[j];
            for (int k = j + 1; k < nums.size(); ++k) {
                if(nums[k] > base){  // 当nums[k] > base时，分叉
                    result = std::max(
                            getNum(k, res + 1),  // 分叉的时候我们需要它继承上阶段的结果
                            result  // 在他结束的时候收回他的结果，并和result进行比较。
                            );
                }
            }
            return res;
        };


        for(int i = 0; i < nums.size(); ++i){
            getNum(i, 1);
        }

        return result;
    }
};

下面的写法也是一样的算法：

class Solution {
    int dfs(vector<int>& nums, int inx, int len, int preval){
        int maxlen = len;

        for (int i = inx; i < nums.size(); ++i) {
            if(nums[i] > preval){
                maxlen = std::max(maxlen, dfs(nums, i + 1, len + 1, nums[i]));
            }
        }

        return maxlen;
    }
public:
    int lengthOfLIS(vector<int>& nums) {
        return dfs(nums, 0, 0, INT_MIN);
    }
};

扩展

最长「不递减] 子序列 的长度

思考1. 如果小改一下题目条件，求 最长「不递减」子序列 的长度呢？

分析：注意「不递减」与 「严格递增」的区别，它允许子序列中存在相邻相同的元素，如 [1,1,2,2,3,3] 是一个不递减的序列。

解答：

• 可以按照上面的思路，将dp[i]定义为长度为i的[不递减]子序列的最小尾数。
• 这样定义的 d 和此前定义的 d 有点小不同，这里的 d 不是严格递增的，但它是不递减的。也就是说，d 可以存在相邻的相同元素，如 $d=[1,1,2,2,2,3,3]$。那么，如果我们要添加一个元素 3，那么应该添加到 最后一个 3 的 后面，以得到最长的子序列。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> minnums;
        for(int v : nums)
        {
            auto pos = upper_bound(minnums.begin(), minnums.end(), v);
            if(pos == minnums.end()) {
                minnums.push_back(v);
            } else {
                *pos = v;
            }
        }
        return minnums.size();
    }
};

最长「递增」子序列 的个数

树状数组

参考

• 一步一步推导出官方最优解法，详细图解
• 超详细图解 递归+动态规划+二分 300. 最长上升子序列
• 穿上衣服我就不认识你了？来聊聊最长上升子序列
• 递归&&DP
• 蜘蛛纸牌