有向无环图的最短路径

最新推荐文章于 2024-05-24 21:53:10 发布

empty_coder

最新推荐文章于 2024-05-24 21:53:10 发布

阅读量2.4k

点赞数 1

分类专栏：计算机算法设计与分析(王晓东) 文章标签：图邻接表拓扑排序 c c++

本文链接：https://blog.csdn.net/emptycodervblog/article/details/54863591

版权

计算机算法设计与分析(王晓东) 专栏收录该内容

2 篇文章 0 订阅

订阅专栏

给定一个有向无环图和源点s,并求s到其它各顶点的最短路径,在图中无负边时,通常采用Dijkstra算法（O(V^2)）; 有负边是则采用Bellman-Ford算法(O(VE));均无法在线性时间内得到结果,而如果先对邻接表结构的有向图采用拓扑排序,得到排序后的数组print，然后从源点开始更新邻接结点的最小路径,最终可得到源点到其它所有结点的最短路径

关于拓扑排序，核心是先将所有入度为0的结点入栈,然后依次出栈(用print数组保存),同时将邻接结点入度减1(减为0时要入栈)

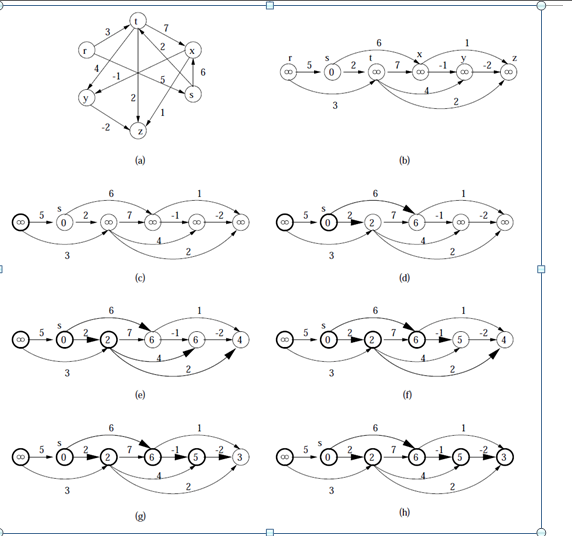
下面这张图很好地显示了具体的流程：

下面的C代码采用的是上面的算法

#include <stdio.h>
#include <stdlib.h>
#include <string.h> 
#define MaxSize 1000
#define TRUE 1
#define FALSE 0 
#define INF 0x3f3f3f3f//1061109567 
//typedef int VertexType;
//边表结点
typedef struct arcnode{
	int adjvex; //邻接点域,存储顶点对应的下标 
	int weight; 
	struct arcnode *nextarc; //邻域,指向下一个邻接点 
}ArcNode;

//顶点表
typedef struct{
//	VertexType data;
	ArcNode *firstarc; //边表头结点 
}VNode; 

//邻接表定义
typedef struct{
	VNode adjlist[MaxSize];
	int n,e;
}AGraph;

//顺序栈
typedef struct{
	int top;
	int data[MaxSize];
}SqStack;

int indegree[MaxSize],print[MaxSize],min_dis[MaxSize];//print为拓扑排序后的结果 

void InitStack(SqStack *S){  
    S->top = -1;   
}  
void Push(SqStack *S,int i){  
    S->data[++(S->top)] = i;  
}  
void Pop(SqStack *S,int *i){  
    *i = S->data[S->top--];  
}  
int IsEmpty(SqStack S){  
    if(S.top == -1)  
        return TRUE;  
    else{  
        return FALSE;  
    }  
} 

void CreateGraph(AGraph *G){
	int tail,head,w;
	for( int i = 0 ; i < G->n ; i ++ ) //初始化顶点表指针 
		G->adjlist[i].firstarc = NULL;
	for( int i = 0 ; i < G->e ; i ++ ){
		scanf("%d%d%d",&tail,&head,&w);
		indegree[head] ++;
		//头插法 
		ArcNode *p = (ArcNode *)malloc(sizeof(ArcNode));
		p->nextarc = G->adjlist[tail].firstarc;
		G->adjlist[tail].firstarc = p;//
		p->adjvex = head;
		p->weight = w;
	}
}

void TopologicalSort(AGraph G){
	SqStack S; //用栈或队列都可以
	InitStack(&S);
	for( int i = 0 ; i < G.n ; i ++ )
		if(!indegree[i])
			Push(&S,i);
	int count = 0;
	while(!IsEmpty(S)){
		int index;
		Pop(&S,&index);
		print[count ++] = index;
		for(ArcNode *p = G.adjlist[index].firstarc ; p ; p = p->nextarc){
			if(!(-- indegree[p->adjvex]))
				Push(&S,p->adjvex);
		}
	}
}

void ShortestPath(AGraph G,int s){
	int index;
	for(int i = 0 ; i < G.n ; i ++ )
		if(print[i] == s){
			index = i;
			break;
		}
	//更新最小路径长度(如果要记载具体路径,记住前驱结点即可,初始化均为源点) 
	int s1;
	for(int i = index ; i < G.n ; i ++ ){//源点前面的结点到源点距离固定为INF
		s1 = print[i] ;
		for(ArcNode *p = G.adjlist[s1].firstarc ; p ; p = p->nextarc){
			if(min_dis[p->adjvex] > min_dis[s1] + p->weight)
				min_dis[p->adjvex] = min_dis[s1] + p->weight;
		}
	}
	//ShowPathLen
	for( int i = 0 ; i < G.n ; i ++ ){
		printf("%d->%d:",s,print[i]);
		if(min_dis[i] == INF)
			printf("INF\n");
		else printf("%d\n",min_dis[i]);
	}
}

int main(){
	AGraph G;
	while(~scanf("%d%d",&G.n,&G.e)){
		memset(indegree,0,sizeof(indegree));
		CreateGraph(&G);
		TopologicalSort(G);
		int s;
		scanf("%d",&s);
		memset(min_dis,INF,sizeof(min_dis[0])*(G.n));
		min_dis[s] = 0;
		ShortestPath(G,s);
	}
	return 0;
}

下面的C++代码参照的是最下面的网址上的代码

#include <iostream>
#include <list>
#include <cstring>
#include <stack>
const int INF = INT_MAX;
using namespace std;

//邻接表结点 
class AdjacentListNode{
	int v;
	int w;
public:
	AdjacentListNode(int _v,int _w){ //带参构造函数
		v = _v , w = _w ;
	}
	int GetNode() { return v; }
	int GetWeight() { return w; }
};

//图 
class Graph{
	int V; 
	list<AdjacentListNode> *adj;
	void TopologicalSort(int v, bool visited[], stack<int> &stk); // 
public:
	Graph(int V); //构造函数一般public 
	void AddEdge(int u, int v, int w);
	void ShortestPath(int s);
};

Graph::Graph(int V){ //构造函数不返回任何值 
	this->V = V;
	adj = new list<AdjacentListNode>[V]; //V个边表结点指针 
}

void Graph::AddEdge(int u, int v, int w){
	AdjacentListNode node(v,w); //实类化对象 
	adj[u].push_back(node);
}

void Graph::TopologicalSort(int v, bool visited[], stack<int> &stk){  
	visited[v] = true;
	for(list<AdjacentListNode>:: iterator i = adj[v].begin() ; i != adj[v].end() ; i ++ ) {
		if(!visited[i->GetNode()])
			TopologicalSort(i->GetNode(),visited,stk);
	}
	stk.push(v);//图的后继结点 必后入栈 
}

void Graph::ShortestPath(int s){
	stack<int> stk;
	int min_dis[V]; //不需要动态开辟
	bool visited[V];
	memset(visited,false,sizeof(visited));
//	memset(min_dis,INF,sizeof(min_dis)); //-1
	for(int i = 0 ; i  < V ; i ++ )
		min_dis[i] = INF;
	min_dis[s] = 0;
	//拓扑排序 
	for(int i = 0; i < V ; i ++ )
		if(!visited[i])
			TopologicalSort(i,visited,stk);
	//求最短路径
	while(!stk.empty()) {
		int u = stk.top();
		stk.pop();
		//更新所有相邻的结点
		list<AdjacentListNode>:: iterator i; //迭代器(指针作用) 
		if(min_dis[u] != INF){ //0之前为INF的都自动略过 
			for(i = adj[u].begin(); i != adj[u].end() ; i ++ ){
				if(min_dis[i->GetNode()] > min_dis[u] + i->GetWeight())	
					min_dis[i->GetNode()] = min_dis[u] + i->GetWeight();
			}
		
		}
	}
	for(int i = 0 ; i < V ; i ++ )
		(min_dis[i] == INF) ? cout << "INF " : cout << min_dis[i] << " ";
} 

int main(){
	Graph g(6); 
	g.AddEdge(4,5,-2);
	g.AddEdge(0,1,5);
	g.AddEdge(0,2,3);
	g.AddEdge(1,3,6);
	g.AddEdge(1,2,2);
	g.AddEdge(2,4,4);
	g.AddEdge(2,5,2);
	g.AddEdge(2,3,7);
	g.AddEdge(3,4,-1);
	int s = 1;
	cout << "Following are the shortest distances from source:" << endl;
	g.ShortestPath(s);
	return 0;
}

测试样例:

6 9

4 5 -2

0 1 5

0 2 3

1 3 6

1 2 2

2 4 4

2 5 2

2 3 7

3 4 -1

6 9