【模板】树状数组 区间修改，区间求和 （模板题：洛谷P3372线段树1）

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

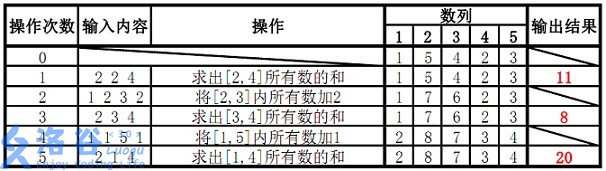
样例说明：

#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;

ll n,m;
ll a[500000],c[500000],c2[500000];


ll lowbit(ll x){
	return x&(-x);
}

ll sigma(ll *r,ll x){    //树状数组的优势，log(n)求前x项的和 
	ll s=0;
	for (ll i=x;i>0;i-=lowbit(i)) s+=r[i];
	return s;
}

void add(ll *r,ll x,ll v){  //向上打标记 
	for (ll i=x;i<=n;i+=lowbit(i)) r[i]+=v;
}

ll ask(ll x,ll y){          //询问区间和 
	ll s1=y*sigma(c,y)-sigma(c2,y);
	ll s2=(x-1)*sigma(c,x-1)-sigma(c2,x-1);
	return s1-s2;
}

int main(){
	scanf("%lld%lld",&n,&m);
	ll flag,x,y,v;
	for (ll i=1;i<=n;++i){
		scanf("%lld",a+i);
		add(c,i,a[i]-a[i-1]);
		add(c2,i,(i-1)*(a[i]-a[i-1]));
	}
		
	for (ll i=1;i<=m;++i){
		scanf("%lld",&flag);
		if (flag==1){
			scanf("%lld%lld%lld",&x,&y,&v);
			add(c,x,v);        //差分思想 
			add(c,y+1,-v);     //在维护两个数组时 
			add(c2,x,(x-1)*v); //在点上打上标记 
			add(c2,y+1,-v*y);
		}else
		if (flag==2){
			scanf("%lld%lld",&x,&y);
			printf("%lld\n",ask(x,y));
		}
	}
	return 0;
}