一、树的概念及结构
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树有一个特殊的节点,叫做根节点,因为根节点没有前驱节点。
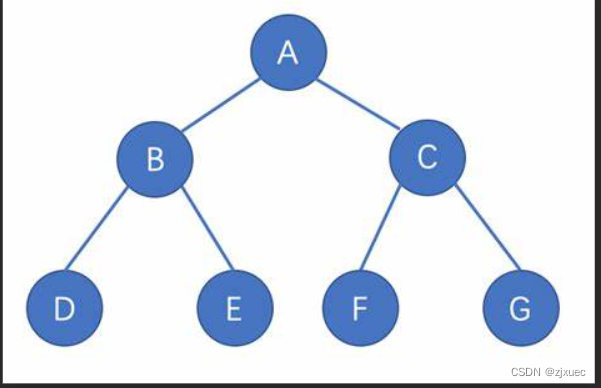
如上图所示,A节点就是该二叉树的根节点,除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继,因此,树是递归定义的。
这里我们要注意的是,在一个树中他的子树是不能够有交集的,如果有交集那么它就不是一个树。
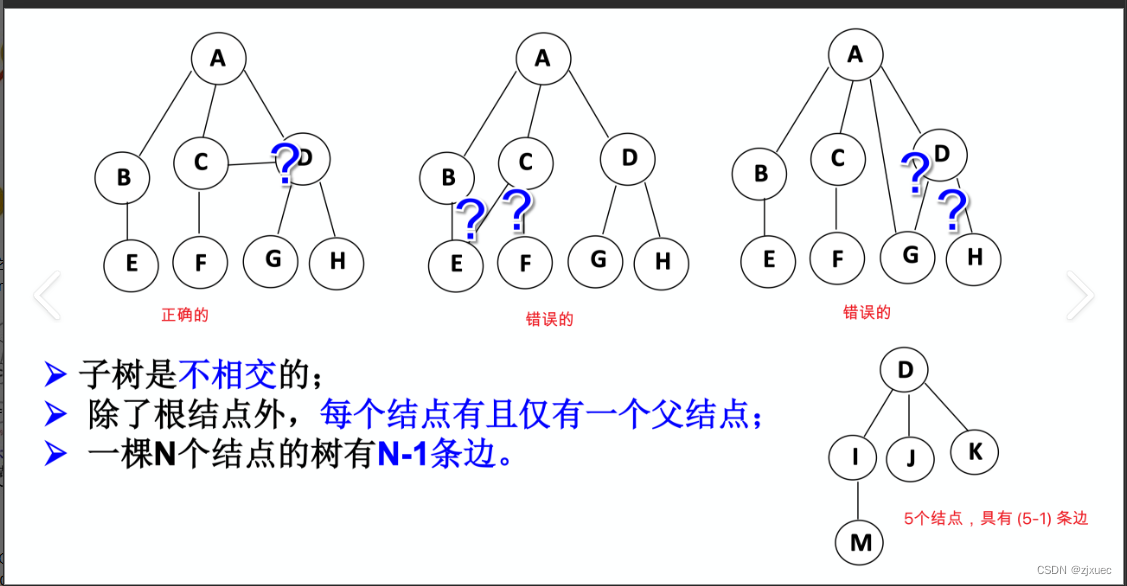
如上图所示,如果一棵树的子树有交集,那么它就不是一棵树,而且除了根节点以外,每个节点有且只有一个父节点,有N个节点的树有N-1条边,这些都是树的一些基本的性质,我们记住就好。
1.2 树的相关概念
我们通过一个树的图来配合我们进行理解。
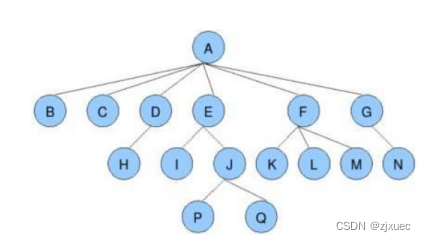
1.节点的度:一个节点含有的子树的个数称为该结点的度。配合着上图来看A节点的度就为6,简单理解也可以看该节点有多少个孩子,有几个孩子度就为多少。
2.叶节点或终端节点:度为0的结点称为叶节点。配合上图来看B、C、H、I、J...等节点都是叶子节点,简单理解就是如果该节点没有孩子,那么他就是叶子节点。
3.非终端节点或分支节点:度不为0的节点。 配合上图来看D、E、F、G...等节点为分支结点,简单理解就是除根节点之外有孩子的节点。
4.双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的节结点。配合上图来看,A是B的父节点,D是H的父节点...
5.孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。配合上图来看,B是A的子节点,H是D的子节点...
6.兄弟节点:具有相同父结点的结点互称为兄弟结点。配合上图来看,B和C是兄弟节点、I和J是兄弟节点...
7.树的度:一棵树中,最大的节点的度称为树的度。配合上图来看,该树的度为6。
8.节点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推。
9.树的高度或深度:树中结点的最大层次。配合上图来看,该树的深度为4。
10.森林:由m(m>0)棵互不相交的树的集合称为森林。
1.3树在实际中的运用
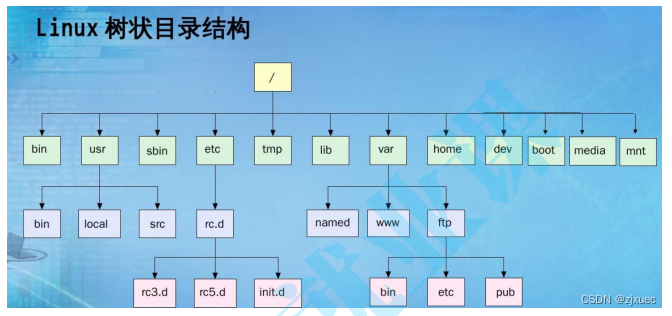
用于表示文件系统的目录树结构。
二、二叉树的概念和结构
2.1 二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根结点加上两棵别称为左子树和右子树的二叉树组成
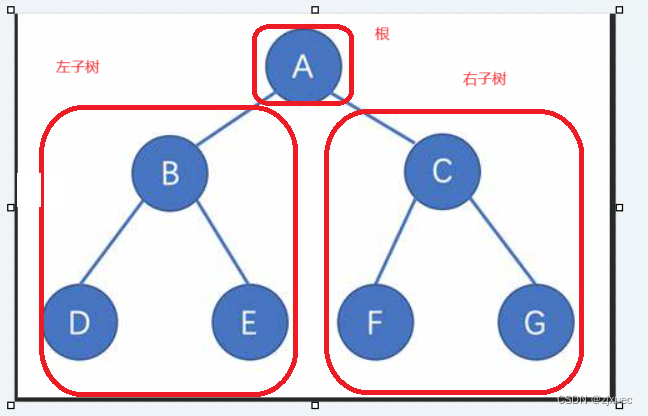
从上图可以看出:
1. 二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
这里需要注意的是,对于任何一种二叉树,他都是由以下这几种情况复合而成的。
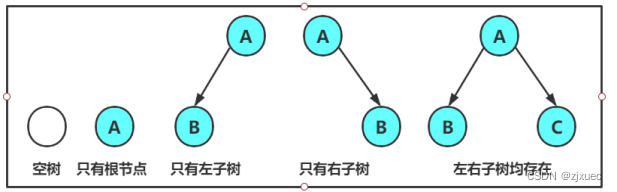
2.2 特殊的二叉树
2.2.1 满二叉树
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^K)-1 ,则它就是满二叉树。
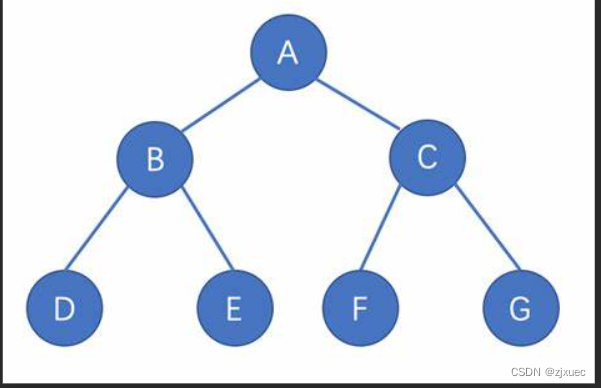
上图就是一个满二叉树。
2.2.2 完全二叉树
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
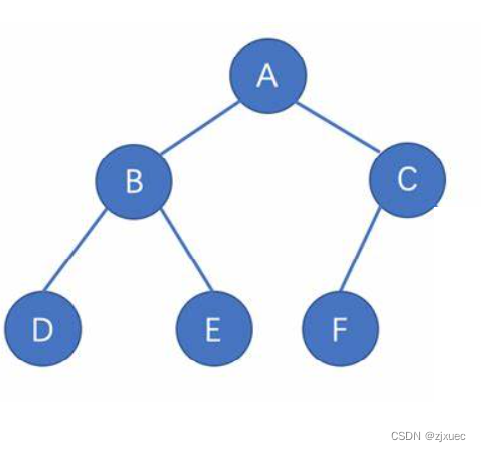
上图就是一个完全二叉树,如果最后一层的节点从左到右必须要一一对应。最后剩一个单独的左节点而没有右节点也是可以的。
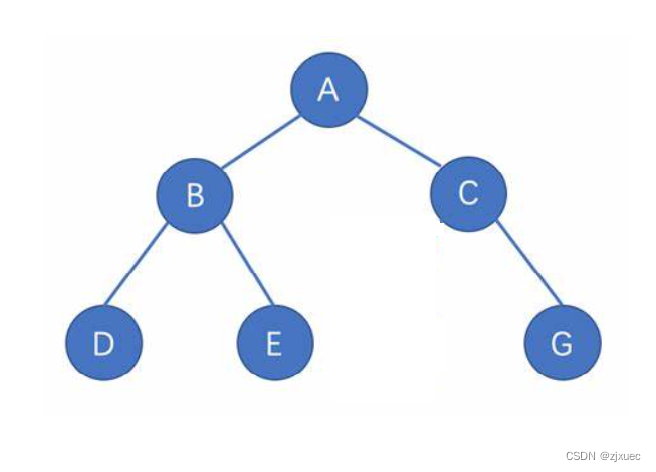
对于这种情况来说,他就不是一个完全二叉树,他的左右节点并没有一一对应。
对于满二叉树而言,慢二叉树的最后一层的节点是满的,也满足一一对应的条件,所以说满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
我们一样根据一个二叉树的图来配合我们进行理解。
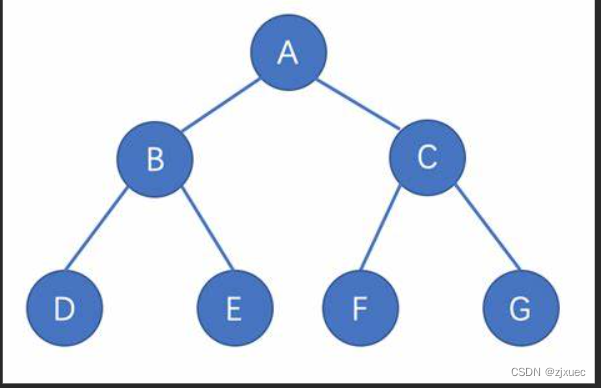
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个节点.。第一层为2^(1-1)个节点,第二层为2^(2-1)个节点,以此类推,从上图来看应该很容易理解。
2.若规定根结点的层数为1,则深度为h的二叉树的最大结点数是(2^h)-1。二叉树的最大节点数即为满二叉树的节点数,上图便是一个满二叉树,深度h为3,(2^3)-1=7,符合上图的节点个数。
3.对任何一棵二叉树, 如果度为0其叶结点个数为N0 , 度为2的分支结点个数为N2 ,则有 N0=N2+1。根据上图来推就好了。
4.若规定根结点的层数为1,具有N个结点的满二叉树的深度,h=log2(N+1)(ps:是log以2 为底,n+1为对数)。自己带入算一下就好了。
5.对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从0开始编号,则对 于序号为i的结点有:
1. 若i>0,i位置结点的双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点。
2. 若2i+1=n否则无左孩子 3. 若2i+2=n否则无右孩子。
这些都是二叉树的基本性质,记住就好了,也可以自己画图带进去算,加强理解。
2.4 二叉树的存储
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
2.4.1 二叉树的顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
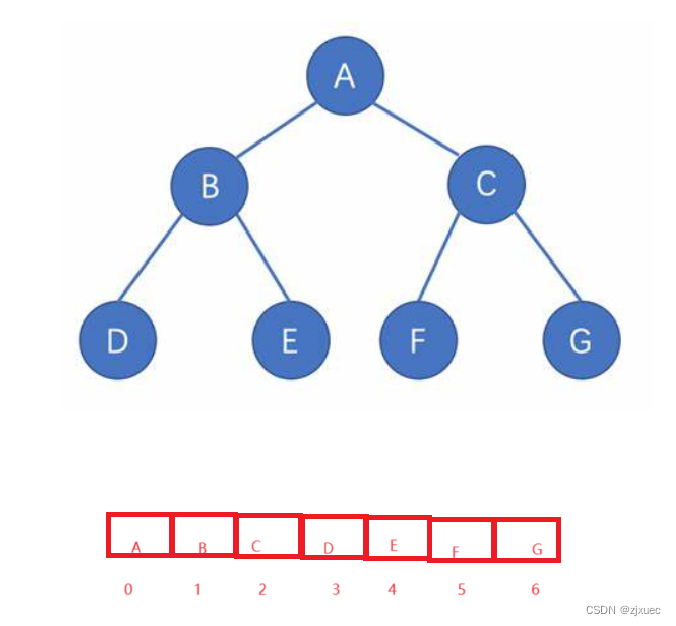
这便是完全二叉树用数组存储后的结果,通过数组的下标和之前讲的二叉树的性质,我们可以很快找出一个节点的父节点和左右子节点。
2.4.2 二叉树的链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。
我们通常使用二叉链来存储二叉树,数据域用来存放数据,左右指针域指向左右子节点。
二叉链的结构体声明:
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* left; // 指向当前结点左孩子
struct BinTreeNode* right; // 指向当前结点右孩子
BTDataType data; // 当前结点值域
}
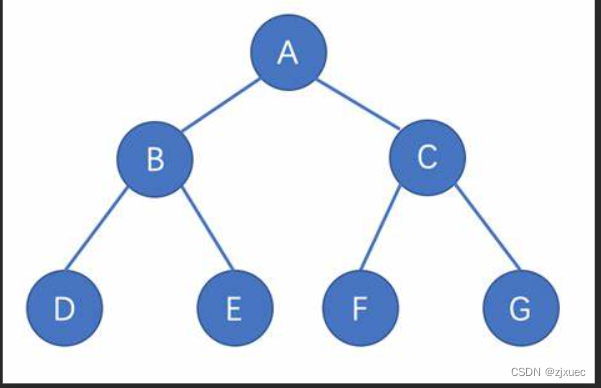
链式存储的二叉树基本上就和上图一样,左右指针指向左右子节点。
三、二叉树的顺序结构及实现
3.1 二叉树的顺序结构
上面我们说过普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
这里我们引入了一个新的概念叫堆,堆也是一种二叉树,但比一般的二叉树更加特别。下面我们来解释一下堆。
3.2 堆的概念和结构
3.2.1 堆的概念
堆分为大堆和小堆,小堆的特点是根节点的值小于等于他的子节点的值,大堆的特点是根节点的值大于等于他的子节点的值,而对于子节点的大小关系没有要求。所以,小堆的根节点一定是最小的,大堆的根节点一定是最大的。
小堆:
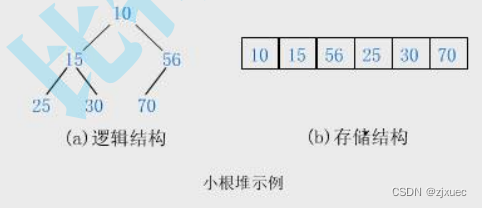
大堆:
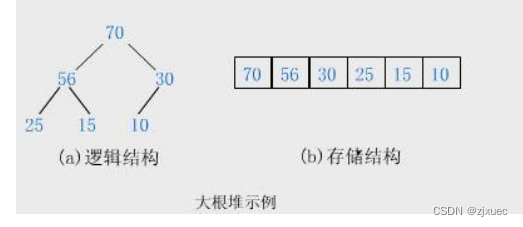
3.2.2 堆的性质
1.堆中某个结点的值总是不大于或不小于其父结点的值。
2.堆总是一棵完全二叉树。
3.3 堆的实现
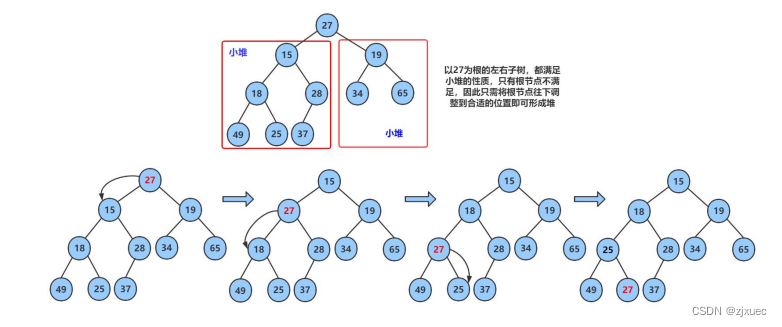
3.3.1 向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根结点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
向下调整算法代码:
//交换位置
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType temp = *a;
*a = *b;
*b = temp;
}
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;//找到左孩子
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])
{
child++;//比较左右孩子的大小,谁小谁与父节点交换
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);//交换父子节点
parent = child;
child = parent * 2 + 1;//寻找下一个左孩子,向下继续调整
}
else
{
break;
}
}
}
3.4 堆的创建
我们一般给出的数组都不是堆,所以我们要将其调整为堆,那么该如何调整呢?这里我们从倒数的第一个非叶子结点的 子树开始调整,一直调整到根结点的树,就可以调整成堆。
void create_heap(int*a ,int n)
{
int end = n - 1;
int i = 0;
for (i = (end - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
}
int main()
{
int a[] = { 2,4,6,1,2,9,7,4,0,4,2,3,4 };
create_heap(a, sizeof(a) / sizeof(a[0]));
return 0;
}
这便是向下调整建堆,一直调整到根节点,每次都找树中的一个节点的父母进行调整,从最后一个节点开始调整,到根结束,这样便创建出了一个堆。
当然我们也可以用向上调整的方式来建堆,但向下调整方式建堆的时间复杂度更优,所以我们采用向下调整方式建堆。向上调整的时间复杂度为O(NlogN),向下调整的时间复杂度为O(N)。
3.4 堆的功能实现
堆的结构体声明:
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
a是数组,_size用来记录数组里面的元素个数,_capacity表示数组的容量。
3.4.1 堆的初始化
//堆的初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_size = hp->_capacity = 0;
}
将数组置为空,_size和_capacity置为0。
3.4.2 堆的插入
堆的插入就是将数据插入到数组尾部,因为插入了元素可能会破坏堆的结果,所以我们还需要对其进行向上调整,使其恢复堆的性质。
向上调整算法:
//向上调整算法
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;//找父节点
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);//如果孩子比父亲小就要交换
child = parent;
parent = (child - 1) / 2;//再向上进行查找调整
}
else
{
break;//孩子大于父亲说明不需要进行调整
}
}
}
堆的插入:
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->_size == hp->_capacity)//判断是否需要扩容
{
int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->_a, newcapacity * sizeof(HPDataType));
//动态创建数组
if (tmp == NULL)
{
perror("realloc fail");
return;
}
hp->_a = tmp;
hp->_capacity = newcapacity;
}
hp->_a[hp->_size] = x;//赋值
hp->_size++;//插入完后_size++
AdjustUp(hp->_a, hp->_size - 1);//向上调整
}
3.4.3 堆的删除
堆的删除就是就是将堆顶的数据与最后一个数据进行交换,然后将最后一个数据删除掉,最后进行向下调整,使其重新变为堆。
堆的删除:
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp && hp->_size > 0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);//交换堆顶元素和最后一个元素
hp->_size--;//_size--即删除最后一个元素
AdjustDown(hp->_a, hp->_size, 0);//向下调整
}
3.4.4 获取堆顶的数据
直接将数组首元素返回即可。
获取堆顶的数据:
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp && hp->_size > 0);
return hp->_a[0];
}
3.4.5 获取堆的数据个数
直接将_size返回即可。
获取堆的数据个数:
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->_size;
}
3.4.6 堆的判空
我们可以通过_size来判断堆是否为空,如果_size为0,堆就为空,否则就不为空。
堆的判空:
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
return hp->_size == 0 ? 1 : 0;
}
3.4.7 堆实现的完整代码
Heap.h文件:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//向上调整算法
void AdjustUp(HPDataType* a, int child);
//交换位置
void Swap(HPDataType* a, HPDataType* b);
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent);
//打印
void print(Heap* hp);
Heap.c文件:
#include"Heap.h"
//堆的初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_size = hp->_capacity = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->_a);
hp->_a = NULL;
hp->_size = hp->_capacity = 0;
}
//交换位置
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType temp = *a;
*a = *b;
*b = temp;
}
//向上调整算法
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->_size == hp->_capacity)
{
int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->_a, newcapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
hp->_a = tmp;
hp->_capacity = newcapacity;
}
hp->_a[hp->_size] = x;
hp->_size++;
AdjustUp(hp->_a, hp->_size - 1);
}
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])
{
child++;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp && hp->_size > 0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
hp->_size--;
AdjustDown(hp->_a, hp->_size, 0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp && hp->_size > 0);
return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
return hp->_size == 0 ? 1 : 0;
}
//打印
void print(Heap* hp)
{
assert(hp);
int i = 0;
for (i = 0; i < hp->_size; i++)
{
printf("%d ", hp->_a[i]);
}
printf("\n");
}
Test.c文件:
#include"Heap.h"
void test1()
{
int a[] = { 1,2,3,7,5,6,8,0,5,6,1 };
int i = 0;
Heap hp;
HeapInit(&hp);
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(&hp, a[i]);
}
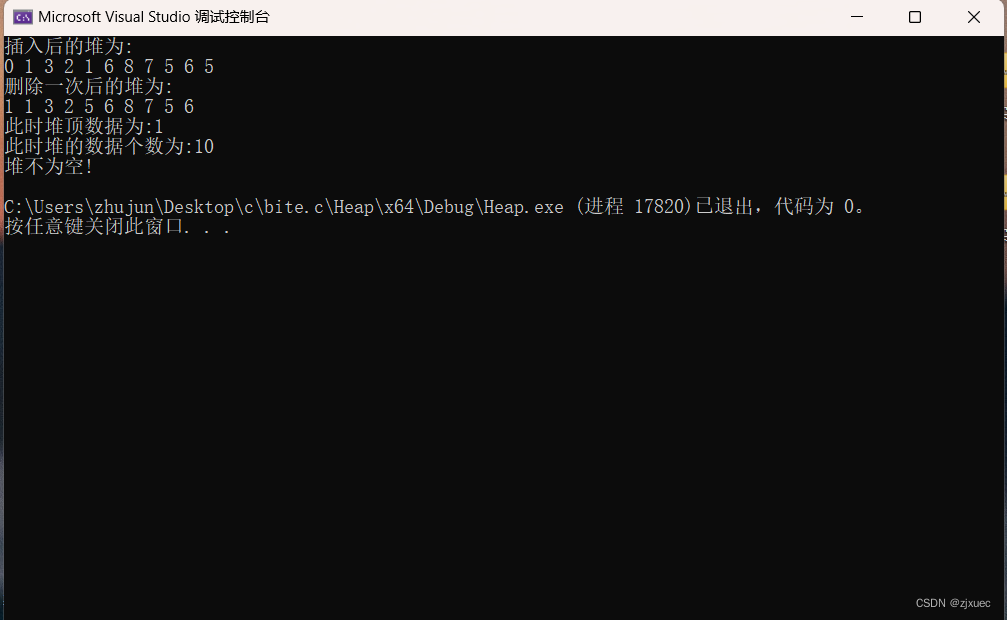
printf("插入后的堆为:\n");
print(&hp);
HeapPop(&hp);
printf("删除一次后的堆为:\n");
print(&hp);
printf("此时堆顶数据为:%d\n", HeapTop(&hp));
printf("此时堆的数据个数为:%d\n", HeapSize(&hp));
int ret = HeapEmpty(&hp);
if (ret == 1)
{
printf("堆为空!\n");
}
else
{
printf("堆不为空!\n");
}
HeapDestory(&hp);
}
int main()
{
test1();
return 0;
}
结果:
四、堆的应用
4.1 堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1.建堆(升序建大堆,降序建小堆)。
2.利用向下调整的思想来排序,每交换一次,就先将最大的(最小的)换到最后,再向下调整建堆,再交换,便将次大的(次小的)换到倒数第二个,换到最后便是进行排序。
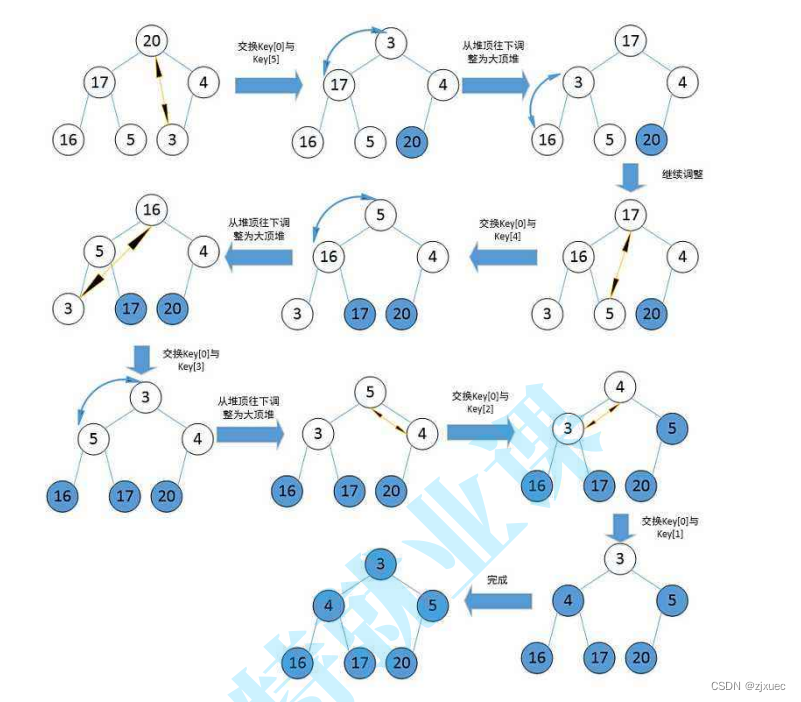
上图便是堆排序的流程图。
结果:
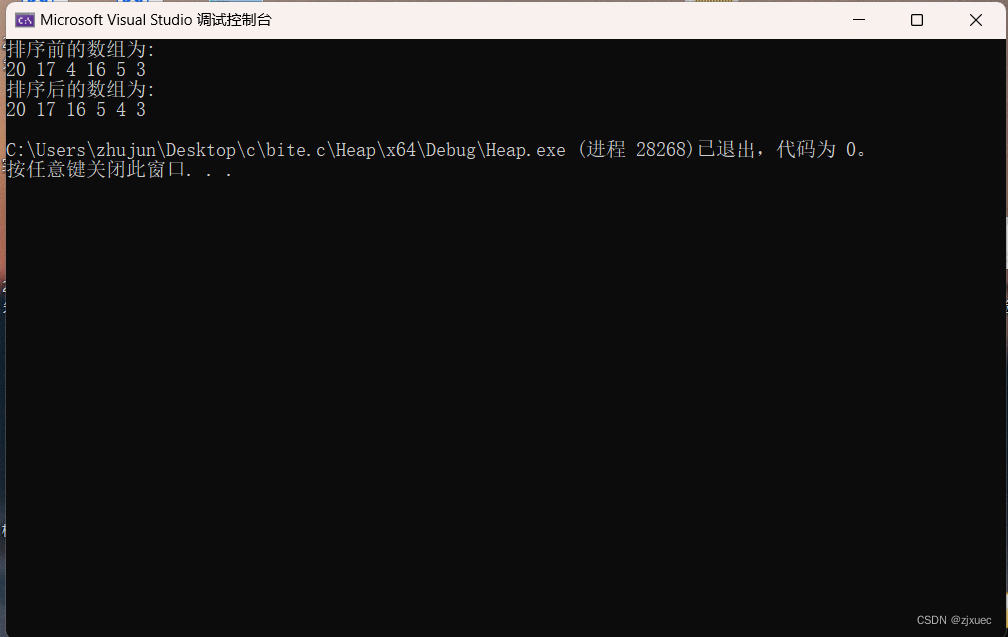
堆排序代码:
// 对数组进行堆排序
void HeapSort(int* a, int n)
{
int end = n - 1;
int i = 0;
for (i = (end - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
int main()
{
int a[] = { 20,17,4,16,5,3 };
int i = 0;
printf("排序前的数组为:\n");
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
printf("%d ", a[i]);
}
printf("\n");
HeapSort(a, sizeof(a) / sizeof(a[0]));
printf("排序后的数组为:\n");
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
4.2 在文件中找TOPK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
解决思路:
1. 用数据集合中前K个元素来建堆:
a.前k个最大的元素,则建小堆
b.前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素 将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
但这样排完序后堆里面的数据虽然是最大的(最小的)前K个数,但堆内的数据并不是有序的,这时我们加个冒泡排序,对排序完后的堆再进行一次排序,得出的结果就是有序的了。
结果:
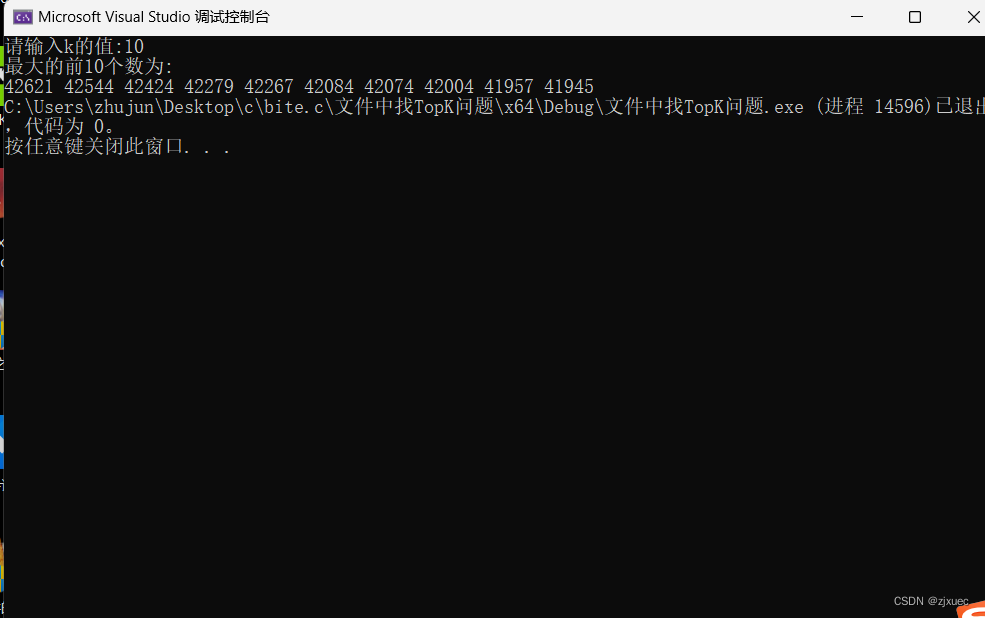
代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void Swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
//向下调整算法
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])
{
child++;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void CreateNDate()
{
// 造数据
int n = 10000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (size_t i = 0; i < n; ++i)
{
int x = (rand()+i) % 1000000;
fprintf(fin, "%d\n", x);//写数据到文件内
}
fclose(fin);
}
void PrintTopK(int k)
{
int i = 0;
int* a = (int*)malloc(sizeof(int) * k);
const char* file = "data.txt";
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen error");
exit(-1);
}
for (i = 0; i < k; i++)
{
fscanf(fout, "%d", &a[i]);//从文件中读取数据并存放到数组中
}
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, k , i);//向下调整建堆
}
int x = 0;
while (!feof(fout))//剩余N-K个数与堆顶元素进行比较,大于堆顶元素便交换
{
fscanf(fout, "%d", &x);
if (x > a[0])
{
a[0] = x;
AdjustDown(a, k, 0);//交换完后向下调整重新成堆
}
}
//冒泡排序重新排序使堆内数据有序
for (i = 0; i < k; i++)
{
int j = 0;
for (j = 0; j < k - 1 - i; j++)
{
if (a[j] < a[j + 1])
{
Swap(&a[j], &a[j + 1]);
}
}
}
printf("最大的前%d个数为:\n", k);
for (i = 0; i < k; i++)
{
printf("%d ", a[i]);
}
}
int main()
{
//CreateNDate();//造数据
int k = 0;
printf("请输入k的值:");
scanf("%d", &k);
PrintTopK(k);
return 0;
}
五、二叉树链式存储的实现
5.1 二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
5.1.1 二叉树的前序遍历
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。即先访问根节点,再访问左子树,最后访问右子树。
代码:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
二叉树的基本操作基本上都是通过递归来实现的,而递归较难理解,这里给出一个递归图给大家理解一下。
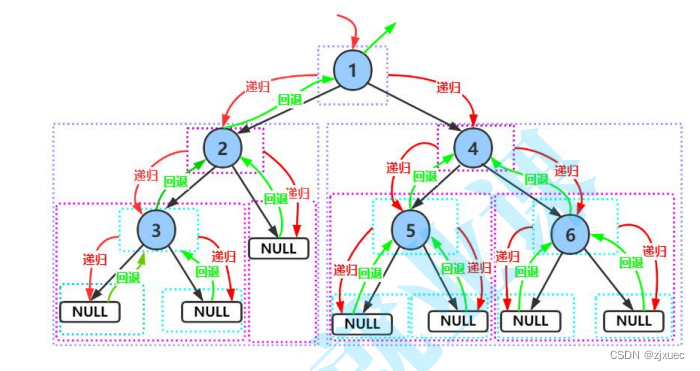
5.1.2 二叉树的中序遍历
2.中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。即先访问左子树,再访问根节点,最后访问右子树。
代码:
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
5.1.3 二叉树的后序遍历
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。即先访问左子树,再访问右子树,最后访问根节点。
代码:
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePostOrder(root->_left);
BinaryTreePostOrder(root->_right);
printf("%c ", root->_data);
}
可以看出,这三种遍历方式是极其相似的,只是访问根节点和左右子树的顺序不同而已,他们的递归图也是十分类似的,大家可以通过前序的递归图来画出和理解中序和后序的递归图。
5.1.4 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
层序遍历想比与前面三个遍历来说十分容易理解,只需一层一层从左往右依次就行了,但实现起来却比前面三个遍历困难,要想实现层序遍历得用到队列。
实现思路:如果根节点不为空,就将该节点插入到队列中,再将该节点出队列并将该节点的左右孩子入队列(左右孩子不为空才能入队列),这样便是层序遍历。
代码:
typedef struct BinaryTreeNode* QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;//队列头指针
QNode* _rear;//队列尾指针
int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->_front = q->_rear = NULL;
q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->_data = data;
newnode->_next = NULL;
if (q->_rear == NULL)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = newnode;
}
q->size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q && q->size > 0);
if (q->size == 1)
{
free(q->_front);
q->_front = q->_rear = NULL;
}
else
{
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
}
q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q && q->size > 0);
return q->_front->_data;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->size == 0 ? 1 : 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while (cur != q->_rear)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->size = 0;
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* temp = QueueFront(&q);
printf("%c ", temp->_data);
if (temp->_left != NULL)
{
QueuePush(&q, temp->_left);
}
if (temp->_right != NULL)
{
QueuePush(&q, temp->_right);
}
QueuePop(&q);
}
QueueDestroy(&q);
}
5.2 二叉树的实现(链式)
5.2.1 二叉树的结构体声明
代码:
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
_data是数据域用于存放数据,结构体指针_left和_right分别指向一个节点的左右孩子节点。
5.2.2 二叉树的创建
代码:
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->_data = a[*pi];
(*pi)++;
newnode->_left = BinaryTreeCreate(a, n, pi);
newnode->_right = BinaryTreeCreate(a, n, pi);
return newnode;
}
数组中的'#'表示NULL,a表示一个数组,n表示数组的大小,但很多人看到int* pi很可能会有疑问,为什么要传一个指针呢? pi是用来给数组记数的,直接传一个整形变量不就好了吗?
但要记住,创建二叉树是用递归来创建的,而递归就离不开一个一个函数的调用,我们都知道函数中的形参是影响不了实参的,如果我们仅仅只简单的传一个整形变量的话,那么pi的值永远改变不了,而形参想要影响实参就必须传入实参的地址,所以这里用int* pi指针来接收。
5.2.3 二叉树的节点个数
代码:
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
如果节点为空返回0,最后递归调用,求左子树的节点个数加右子树的节点个数再加1(根节点),如果一个节点的左右孩子都为空但该节点不为空将会返回1。
5.2.4 二叉树的叶子节点个数
代码:
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL && root->_right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
与求二叉树节点个数的代码有点类似,如果左右孩子都为空的话,那么该节点就是叶子节点,返回1,最后递归调用,求左右子树的叶子节点,不用加上根节点。
5.2.5 二叉树第k层的节点个数
代码:
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
对于一颗树来说,某一层的节点个数就等于其上一层所有节点的左右孩子节点数之和,那么第k层的节点个数就等于k-1层所有节点的左右孩子节点数之和,再对root为空和k为1两种特殊情况进行判断即可得出第k层的节点个数。
5.2.6 二叉树查找值为x的节点
代码:
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* left = BinaryTreeFind(root->_left, x);
if (left != NULL)
{
return left;
}
BTNode* right = BinaryTreeFind(root->_right, x);
if (left != NULL)
{
return right;
}
return NULL;
}
先去根节点找,没找到再去左子树找,最后再去右子树找,利用先序遍历的思想,找到了就返回那个节点,这里需要注意的是,去左右子树进行查找时,一定要对传回来值进行记录,如果不进行记录的话,会增加递归的调用次数,使得程序运行效率大大降低。
5.2.7 判断二叉树是否是完全二叉树
代码:
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* temp = QueueFront(&q);
QueuePop(&q);
if (temp == NULL)
{
break;
}
QueuePush(&q, temp->_left);
QueuePush(&q, temp->_right);
}
while (!QueueEmpty(&q))
{
BTNode* temp = QueueFront(&q);
QueuePop(&q);
if (temp != NULL)
{
return false;
}
}
QueueDestroy(&q);
return true;
}
先将根节点插入队列,再将根节点出队列并将其左右孩子节点入队列,一直循环,直到队列首元素为空,这和层序遍历有点类似,当队列首元素为空时,如果队列中还有非空元素,那么该树就不是完全二叉树,因为完全二叉树的层序遍历如果出现了一个节点为空,且是左孩子先进队列,如果后面队列元素不全为空则不是完全二叉树。
5.2.8 二叉树的销毁
代码:
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->_left);
BinaryTreeDestory(root->_right);
free(root);
}
我们不能先将根节点给free掉,那样就找不到后序的节点了,所以我们采用后序遍历的思想,最后再将根节点free掉。
5.3 二叉树链式存储实现完整代码
BinaryTree.h文件:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
BinaryTree.c文件:
#include"BinaryTree.h"
#include"Queue.h"
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->_data = a[*pi];
(*pi)++;
newnode->_left = BinaryTreeCreate(a, n, pi);
newnode->_right = BinaryTreeCreate(a, n, pi);
return newnode;
}
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->_left);
BinaryTreeDestory(root->_right);
free(root);
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL && root->_right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* left = BinaryTreeFind(root->_left, x);
if (left != NULL)
{
return left;
}
BTNode* right = BinaryTreeFind(root->_right, x);
if (left != NULL)
{
return right;
}
return NULL;
}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePostOrder(root->_left);
BinaryTreePostOrder(root->_right);
printf("%c ", root->_data);
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* temp = QueueFront(&q);
printf("%c ", temp->_data);
if (temp->_left != NULL)
{
QueuePush(&q, temp->_left);
}
if (temp->_right != NULL)
{
QueuePush(&q, temp->_right);
}
QueuePop(&q);
}
QueueDestroy(&q);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* temp = QueueFront(&q);
QueuePop(&q);
if (temp == NULL)
{
break;
}
QueuePush(&q, temp->_left);
QueuePush(&q, temp->_right);
}
while (!QueueEmpty(&q))
{
BTNode* temp = QueueFront(&q);
QueuePop(&q);
if (temp != NULL)
{
return false;
}
}
QueueDestroy(&q);
return true;
}
Queue.h文件:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef struct BinaryTreeNode* QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;//队列头指针
QNode* _rear;//队列尾指针
int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c文件:
#include"Queue.h"
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->_front = q->_rear = NULL;
q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->_data = data;
newnode->_next = NULL;
if (q->_rear == NULL)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = newnode;
}
q->size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q && q->size > 0);
if (q->size == 1)
{
free(q->_front);
q->_front = q->_rear = NULL;
}
else
{
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
}
q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q && q->size > 0);
return q->_front->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q && q->size > 0);
return q->_rear->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
return q->size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->size == 0 ? 1 : 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while (cur != q->_rear)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->size = 0;
}
Test.c文件:
#include"BinaryTree.h"
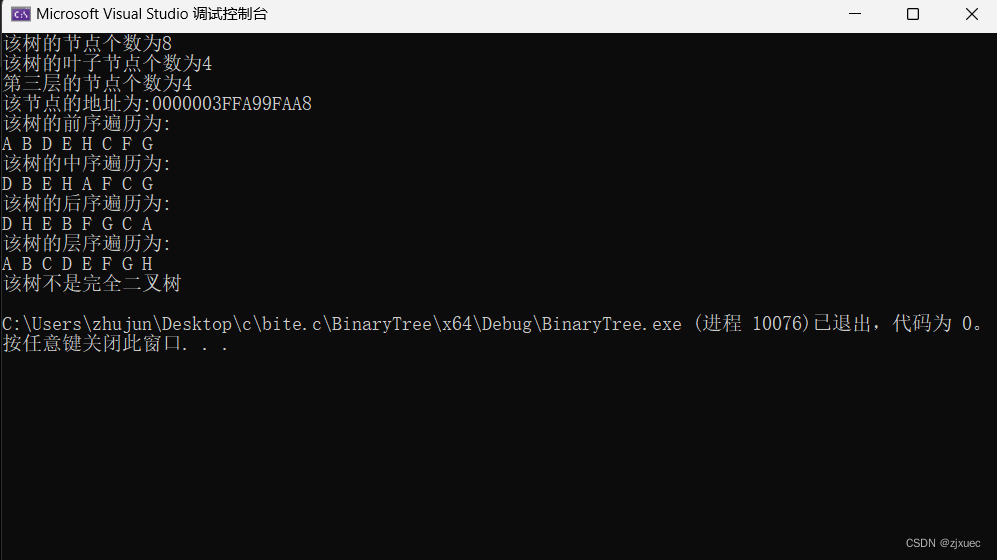
void test(BTDataType* a, int n, int* pi)
{
BTNode* tree = NULL;
tree = BinaryTreeCreate(a, n, pi);
int size=BinaryTreeSize(tree);
printf("该树的节点个数为%d\n", size);
int leafsize = BinaryTreeLeafSize(tree);
printf("该树的叶子节点个数为%d\n", leafsize);
int ksize = BinaryTreeLevelKSize(tree, 3);
printf("第三层的节点个数为%d\n", ksize);
BTNode* find = BinaryTreeFind(tree, 'A');
printf("该节点的地址为:%p\n", &find);
printf("该树的前序遍历为:\n");
BinaryTreePrevOrder(tree);
printf("\n");
printf("该树的中序遍历为:\n");
BinaryTreeInOrder(tree);
printf("\n");
printf("该树的后序遍历为:\n");
BinaryTreePostOrder(tree);
printf("\n");
printf("该树的层序遍历为:\n");
BinaryTreeLevelOrder(tree);
printf("\n");
if (BinaryTreeComplete(tree))
{
printf("该树是完全二叉树\n");
}
else
{
printf("该树不是完全二叉树\n");
}
BinaryTreeDestory(tree);
tree = NULL;
}
int main()
{
char a[] = "ABD##E#H##CF##G##";
int length = sizeof(a) / sizeof(a[0]);
int i = 0;
test(a, length, &i);
return 0;
}
结果:
六、总结
讲到这基本上已经将二叉树的基本概念讲完了,对于二叉树的实现以及递归还是有一定难度的,要自己去画图理解,希望以上所讲能够对你有所帮助,码字不易,有帮助的话记得一键三连哦!感谢各位。




















 3427
3427










