数值积分

1 实验目的

1. 熟悉掌握复化梯形公式和复化Simpson公式，应用这两个公式求定积分的近似解；
2. 会编写用龙贝格算法求定积分的程序。

2 实验内容

1. 分别用复化梯形公式和复化Simpson公式计算下列定积分，通过数值结果比较算法的计算精度。
   (1) $\int_0^1{\frac{1}{1+x^2}}dx$
   (2) $\int_0^1{\frac{\sin(x)}{x}}dx$
2. 用龙贝格方法计算积分
   (1) $\int_0^1{\frac{1}{1+x^2}}dx$
   (2) $\int_0^1{\frac{\sin(x)}{x}}dx$

3 实验程序

被积函数（1）的程序如下所示。

function y = fun1(x)
% 函数(1) f(x) = 1/(1+x^2)
y = 1./(1+x.^2);
end

被积函数（2）的程序如下所示。

function y = fun2(x)
% 函数(2) f(x) = sin(x)/x
y = sin(x)./x;
end

梯形积分程序如下所示。

function y = trap(f, a, b, n)
% 梯形法数值积分
% 输入：f = 函数
%       a = 积分区域下界
%       b = 积分区域上界
%       n = 积分区域分段数
% 输出：y = 积分值
if nargin == 3
    n = 10;
elseif nargin == 1
    a = 0;
    b = 1;
    n = 10;
elseif nargin == 2
    n = a;
    a = 0;
    b = 1;
end
if a == 0
    a = eps;
end
x = linspace(a, b, n+1);
h = abs(diff(x(1:2)));
y = h*(f(x(1)) + f(x(end)) + 2*sum(f(x(2:end-1))))/2;

辛普森（Simpson）积分程序如下所示。

function y = sps(f, a, b, n)
% Simpson 数值积分
% 输入：f = 函数
%       a = 积分区域下界
%       b = 积分区域上界
%       n = 积分区域分段数
% 输出：y = 积分值
if nargin == 3
    n = 10;
elseif nargin == 1
    a = 0;
    b = 1;
    n = 10;
elseif nargin == 2
    n = a;
    a = 0;
    b = 1;
end
if a == 0
    a = eps;
end
t = linspace(a, b, n+1);
h = abs(diff(t(1:2)));
y = h*(f(t(1)) + f(t(end)) ...
    + 4*sum(f(t(1:end-1)+h/2)) ...
    + 2*sum(f(t(2:end-1))))/6;

龙贝格（Romberg）积分程序如下所示。

function [y, ite] = rbgm(f, a, b, TOL, MaxIte)
% Romberg 数值积分
% 调用方法：[y, ite] = rbgm(f, a, b, TOL, MaxIte)
%           [y, ite] = rbgm(f, a, b)
%           [y, ite] = rbgm(f, MaxIte)
%           [y, ite] = rbgm(f)
%
% 输入：f = 函数
%       a = 积分区域下界
%       b = 积分区域上界
%       TOL = 允许误差
%       MaxIte = 最大迭代次数
%
% 输出：y = 积分值
%       ite = 迭代次数
if nargin == 3
    TOL = 1e-6;
    MaxIte = 100;
elseif nargin == 1
    a = 0;
    b = 1;
    TOL = 1e-6;
    MaxIte = 100;
elseif nargin == 2
    MaxIte = a;
    a = 0;
    b = 1;
    TOL = 1e-6;
end
if a == 0
    a = eps;
end
y = 0;
T0 = 0; T1 = 0; S0 = 0; S1 = 0;
C0 = 0; C1 = 0; R0 = 0; R1 = 0;
ite = 0;
x = [a, b];
T0 = (f(a)+f(b))/2;
h = abs(diff(x(1:2)));
while ite < MaxIte
    ite = ite + 1; % 迭代次数 +1
    T1 = T0/2 + h*sum(f(x(1:end-1)+h/2))/2;
    % Simpson
    if ite == 1
        S0 = T1*4/3 - T0/3;
    elseif ite > 1
        S1 = T1*4/3 - T0/3;
    end
    % Cotes
    if ite == 2
        C0 = S1*16/15 - S0/15;
    elseif ite > 2
        C1 = S1*16/15 - S0/15;
    end
    % Romberg
    if ite == 3
        R0 = C1*64/63 - C0/63;
    elseif ite > 3
        R1 = C1*64/63 - C0/63;
    end
    % 误差计算
    if ite == 1
        tol = abs(S0 - T1);
        y = S0;
    elseif ite == 2
        tol = abs(C0 - S1);
        y = C0;
    elseif ite == 3
        tol = abs(R0 - C1);
        y = R0;
    else
        tol = abs(R1 - R0);
        y = R1;
    end
    %误差判定
    if tol < TOL
        return ;
    end
    % 迭代更新
    if ite >= 1
        T0 = T1;
    end
    if ite >= 2
        S0 = S1;
    end
    if ite >= 3
        C0 = C1;
    end
    if ite > 3
        R0 = R1;
    end
    X = zeros(1, length(x)*2-1);
    X(1:2:end) = x;
    X(2:2:end-1) = x(1:end-1) + h/2;
    x = X;
    h = abs(diff(x(1:2)));
end

主程序如下所示。

function main5(num1, num2)
%% 梯形公式
y11 = trap(@fun1, num1);
disp(['y11 = ' num2str(y11)]);
y12 = trap(@fun2, num1);
disp(['y12 = ' num2str(y12)]);
%% 复化 Simpson 公式
S11 = sps(@fun1, num2);
disp(['S11 = ' num2str(S11)]);
S12 = sps(@fun2, num2);
disp(['S12 = ' num2str(S12)]);
%% 龙贝格法
[R21, ite] = rbgm(@fun1, 0, 1);
disp(['R21 = ' num2str(R21)]);
[R22, ite] = rbgm(@fun2, 0, 1);
disp(['R22 = ' num2str(R22)]);

4 实验结果分析

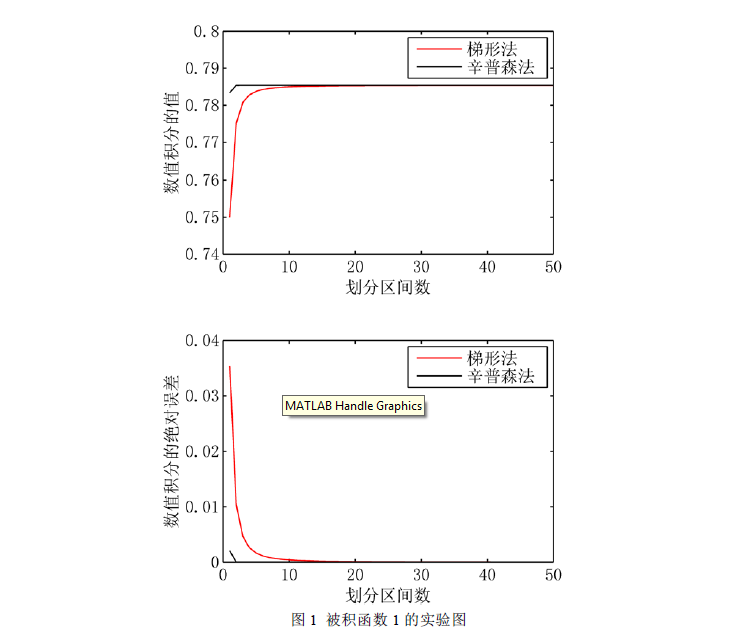
图 1 描述了梯形法和辛普森法对被积函数 1 求数值积分的情况。很显然，辛普森法收敛到满足精度的解所需划分区间的个数比梯形法的更少，由此，不难推断出，辛普森法在该问题上较梯形法更优。

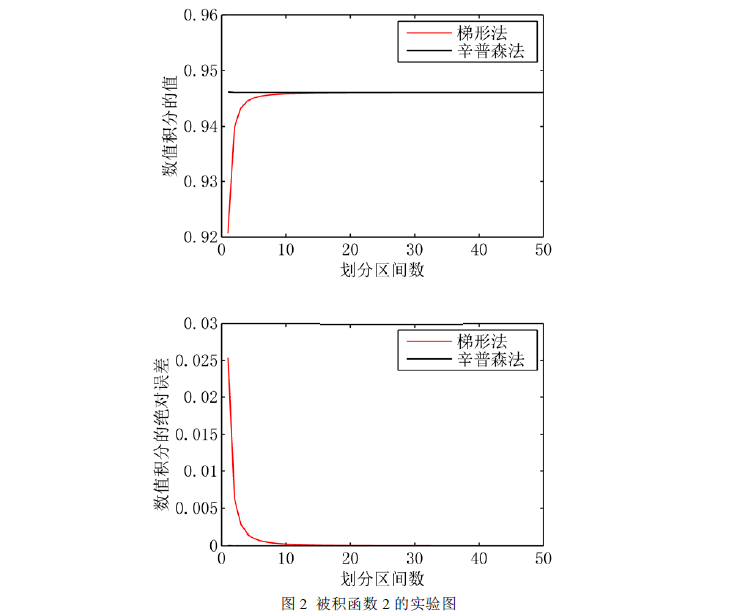
图 2 描述了梯形法和辛普森法对被积函数 2 求数值积分的情况，所示的结果与图 1 相似，且辛普森的收敛速度更快。
龙贝格法对被积函数 1 和被积函数分别用 5 次迭代和 3 次迭代便求得了满足精度要求的结果，其效果比梯形法和辛普森法更优。

5 实验结论

熟悉复化梯形公式、复化 Simpson 公式和龙贝格 Romberg 公式，应用这些方法求解函数的数值积分；掌握了上述 3 种数值积分方法的程序编写方法，并采用 3 种方法在文中提及的问题 （1） 和问题 （2） 做了对比实验，得出了龙贝格数值积分方法较另外 2 种方法的收敛速度更快的结论。