快速排序

简介：

快速排序是一种利用分治思想的排序方法。它的最坏情况时间复杂度为O(n2)的排序算法。虽然最坏情况很差，但是快排通常是实际排序应用中最好的选择，因为它的平均性能非常好；它的期望时间复杂度是O(N * LogN)，而且O(N * LogN)中隐含的常数因子非常小。另外它能够进行原址排序。

基本思想

通过一次 分区操作(Partition) 将需要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别再进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

分区操作(Partition)

Partition是实现将数组中的数据按照基准值大小的规律排列的算法。比如我们要排序某数组中下标从p到r之间的一组数据，可以先选择数组中任意元素当做基准值(Pivot). 一般情况下，我们取数组的最后一个元素当做基准值Pivot. 然后依次遍历从p到r之间的数据，将小于基准值Pivot的数据元素放到基准值Pivot的左边，将大于pivot的值放在其右边，这样就完成了一次分区(Partition)操作。
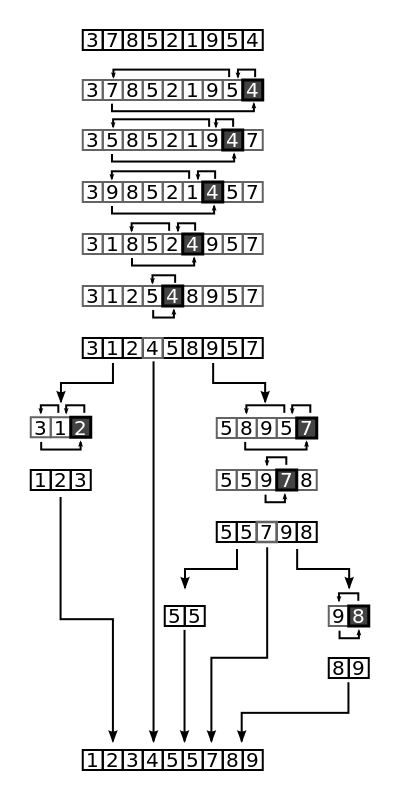
比如需要排序的数组是 [3, 7, 8, 5, 2, 1, 9, 5, 4] 我们选择数组中最后一个元素 4 作为基准值Pivot，经过分区操作之后，数组变为 [3, 1, 2, 4, 5, 8, 9, 5, 7]。 接下来只需要递归的对 4 左右两边的子数组分别再调用Partition操作，一直到子数组的长度为1，数组就完成了所有的排序操作。
这个过程可以参考如下图：

代码实现

如果我们用递推公式将上面的过程写出来的话，就是：

quick_sort(p...r) = quick_sort(p...q-1) + quick_sort(q + 1...r)

如果将地推公式转换为代码则是：

quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

可以看出在快速排序中，最核心的就是分区操作(Partition)的实现, partition的具体实现如下所示：

partition (arr[], low, high)
{
    // pivot (Element to be placed at right position)
    pivot = arr[high];  
 
    i = (low - 1)  // Index of smaller element

    for (j = low; j <= high- 1; j++)
    {
        // If current element is smaller than or
        // equal to pivot
        if (arr[j] <= pivot)
        {
            i++;    // increment index of smaller element
            swap arr[i] and arr[j]
        }
    }
    swap arr[i + 1] and arr[high])
    return (i + 1)
}

代码讲解

比如我们使用快排对数组 [10, 80, 30, 90, 40, 50, 70] 进行排序, 当遍历到一个比基准值(Pivot)小的元素时，需要交换i, j所指向的元素，将比Pivot小的元素放置在Pivot的左边。具体排序的流程如下所示：

原始数组 arr[] = {10, 80, 30, 90, 40, 50, 70}
数组中元素下标分别是: 0 1 2 3 4 5 6
low = 0, high = 6, pivot = arr[high] = 70
定义变量int i = -1， 定义for循环访问变量 int j = low 到 high-1

开始排序
j = 0 : arr[j] <= pivot, 这种情况需要将 i++ 并且交换 i 和 j 指向的元素位置
结果： i = 0; arr[] = {10, 80, 30, 90, 40, 50, 70} // 因为i, j都指向0， 元素位置没有发生改变

j = 1 : arr[j] > pivot, 这种情况不需要执行任何操作
结果： i = 0; arr[] = {10, 80, 30, 90, 40, 50, 70}

j = 2 : arr[j] <= pivot, 执行i++操作 并交换arr[i], arr[j]的位置
结果：i = 1；arr[] = {10, 30, 80, 90, 40, 50, 70} // 交换80 和 30的位置

j = 3 : arr[j] > pivot, 不需要执行任何操作
结果：i = 1；arr[] = {10, 30, 80, 90, 40, 50, 70}

j = 4 : arr[j] <= pivot, 执行i++操作 并交换arr[i], arr[j]的位置
结果：i = 2；arr[] = {10, 30, 40, 90, 80, 50, 70} // 交换80 和 40的位置

j = 5 : arr[j] <= pivot, 执行i++操作 并交换arr[i], arr[j]的位置
结果：i = 3 ；arr[] = {10, 30, 40, 50, 80, 90, 70} // 交换90 和 50的位置

此时 j = 5已经等于high - 1的值，所以for循环执行完毕。这个时候我们需要将arr[i+1] 和 arr[high] (也就是Pivot)位置进行交换，这一步的目的是将Pivot放在所有大于它的数据前面
结果：arr[] = {10, 30, 40, 50, 70, 90, 80} // 交换80和70的位置
到此我们就将所有小于70(Pivot)的数据放在左边，所有大于等于70(Pivot)的数据放在右边了，后续只要递归再分别对左右两边的子数组进行快排操作即可

性能分析

最坏时间复杂度

当待排序的数组为正序或逆序排列时，比如 [90, 80, 70, 50, 40, 30, 10], 我们取数组最后的元素10为Pivot，经过Partition之后的子数组全部在10的右边，结果为 [90, 80, 70, 50, 40, 30, 10] 。然后再次对[90, 80, 70, 50, 40, 30] 调用Partition操作。假设原始待排序的数组长度为N，那么这种情况下我们需要调用 N - 1(从N到2)次Partition操作，并且在每一次Partition操作中都需要执行N - 2次比较大小操作。
所以总结一下公式就是如下：
T(N) = n + (n−1) + (n−2) +⋯+ 2 = (n+1)(n/2)−1
因此最坏时间复杂度为 O(n2)

最好时间复杂度

​在最优情况下，Partition每次都划分得很均匀，如果排序n个关键字，在每次Partition之后两边数组的长度就为 [log2n]，即仅需递归 log2n 次，需要时间为T(n)的话，第一次Partiation应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢轴将数组一分为二，那么各自还需要T(n/2)的时间（注意是最好情况，所以平分两半）。于是不断地划分下去，就有了下面的不等式推断：
T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn;
这说明，在最优的情况下，快速排序算法的时间复杂度为 O(nlogn)

平均时间复杂度

假设每次分区操作(Partition)都将数组分成大小为9 : 1的两个小区间。套用递归时间复杂度的公式就会变成：

T(1) = C; // n = 1, 只需要常量级的执行时间，所以标识为C
=> T(n) = T(n/10) + T(9 * n / 10) + n; // n > 1
这个公式的递推求解过程比较复杂，可以参考算法导论书中的具体推导构成
最后得出平均时间复杂度为 O(nlogn)