会慢慢增加例题,代码主要采用刘汝佳在蓝书上的代码。
文章目录
存储方法
- 点: 直接存储坐标(x,y)
- 直线/线段: 存两个点
- 圆:圆心和半径
- 多边形: 按顺/逆时针存储点
- 向量: 把起点平移到源点,记录终点,存下来也是一个点
向量的缩放可用(x,y)->(kx,ky)表示
注:为了避免分类和误差,避免使用解析几何
代码
struct Point {
double x, y;
Point(double x = 0, double y = 0) : x(x), y(y) {}
};
typedef Point Vector;
精度问题
首先设一个eps(例如1e-8)
- a = = =b: fabs(a-b)<eps
- a ̸ = \not = ̸=b: fabs(a-b)>eps
- a < < <b: a+eps<b
- a > > >b: a<b+eps
代码
//向量+向量=向量,点+向量=点
Vector operator+(Vector A, Vector B) {
return Vector(A.x + B.x, A.y + B.y);
}
//点-点=向量
Vector operator-(Point A, Point B) {
return Vector(A.x - B.x, A.y - B.y);
}
Vector operator*(Vector A, double p) {
return Vector(A.x * p, A.y * p);
}
//向量/数=向量
Vector operator/(Vector A, double p) {
return Vector(A.x / p, A.y / p);
}
bool operator<(const Point& a, const Point& b) {
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
const double eps = 1e-10;
double dcmp(double x) {
if (fabs(x) < eps)
return 0;
else
return x < 0 ? -1 : 1;
}
bool operator==(const Point& a, const Point& b) {
return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}
点积和叉积
点积
- a ⋅ \cdot ⋅ b = = = |a||b| cos θ \cos \theta cosθ ,其绝对值等于a在b上的投影模长乘上b的模长
- (a+b) ⋅ \cdot ⋅c = = =a ⋅ \cdot ⋅c+ b ⋅ \cdot ⋅c
- a ⋅ \cdot ⋅b = = = x 1 x 2 + y 1 y 2 x_1x_2+y_1y_2 x1x2+y1y2
- a ⊥ \perp ⊥c ⇔ \Leftrightarrow ⇔ a ⋅ \cdot ⋅b = = = 0
代码
double Dot(Vector A, Vector B) {
return A.x * B.x + A.y * B.y;
}//点积
double Length(Vector A) {
return sqrt(Dot(A, A));
}//模长
叉积
- a × \times × b = = = |a||b| sin θ \sin \theta sinθ, θ \theta θ表示a旋转到b经过的夹角
- 几何意义:两个向量为相邻边构成平行四边形的面积
- 当b在a左侧时为正(从a逆时针转到b),右侧为负
- (a+b) × \times ×c = = =a × \times ×c+ b × \times ×c
- a × \times × b = x 1 y 2 − x 2 y 1 = x_1y_2-x_2y_1 =x1y2−x2y1
- a 与 b平行 ⇔ \Leftrightarrow ⇔ a × \times × b = 0 =0 =0
应用
- 求平行四边形面积
- 求点到直线的距离
- 利用叉积求出面积
- 除以底边线段长得出高(也就是距离)
代码
double Cross(Vector A, Vector B) {
return A.x * B.y - A.y * B.x;
}//叉积
double DistanceToLine(Point P, Point A, Point B) {
Vector v1 = B - A, v2 = P - A;
return fabs(Cross(v1, v2)) / Length(v1); //如果不取绝对值,得到的是有向距离
} //点到直线的距离
旋转向量
a
=
(
x
,
y
)
=(x,y)
=(x,y)旋转
θ
\theta
θ 得到b
b =
(
x
cos
θ
−
y
sin
θ
,
x
sin
θ
+
y
sin
θ
)
(x\cos \theta - y\sin \theta,x\sin\theta+y\sin\theta)
(xcosθ−ysinθ,xsinθ+ysinθ)
注:套用和角公式得到
代码
//rad是弧度
Vector Rotate(Vector A, double rad) {
return Vector(A.x * cos(rad) - A.y * sin(rad),
A.x * sin(rad) + A.y * cos(rad));
}
求直线的交点
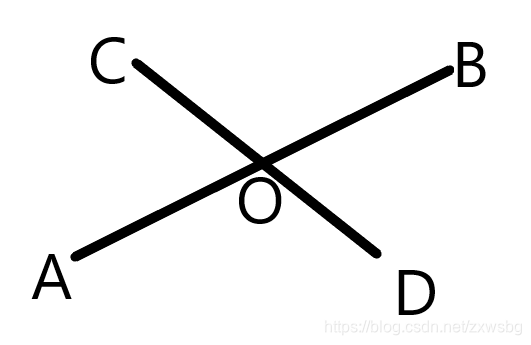
- 用叉积求出 S Δ A C D S_{\Delta ACD} SΔACD和 S Δ B C D S_{\Delta BCD} SΔBCD
- 设 l 1 = A O , l 2 = B O l_1=AO, l_2=BO l1=AO,l2=BO
-
O
=
A
+
(
B
−
A
)
S
1
S
1
+
S
2
O = A + (B-A) \frac{S_1}{S_1+S_2}
O=A+(B−A)S1+S2S1
注意: 需要特判AB × \times ×CD = 0 =0 =0,即两直线是否平行(重合)
代码
//调用前保证两条直线P+tv和Q+tw有唯一交点。当且仅当Cross(v, w)非0
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) {
Vector u = P - Q;
double t = Cross(w, u) / Cross(v, w);
return P + v * t;
}
判断两直线是否相交
- 当CA × \times ×CB与DA × \times ×DB符号一样时,两直线相交
- 由此引申,当CA
×
\times
×CB
<
0
<0
<0时,C在线段AB的左侧
注意:两直线重合需要特判一下坐标
代码
bool SegmentProperIntersection(Point a1, Point a2, Point b1, Point b2) {
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - b1),
c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
return dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0;
}
求多边形的面积
已知一个简单多边形顶点逆时针顺序为
P
1
,
P
2
…
…
,
P
n
P_1,P_2……,P_n
P1,P2……,Pn,那么这个多边形的面积为
1
2
(
P
n
→
×
P
1
→
+
∑
i
=
1
n
−
1
P
i
→
×
P
i
+
1
→
)
\frac{1}{2}(\overrightarrow{P_n}\times \overrightarrow{P_1}\ + \sum\limits_{i=1}^{n-1}\overrightarrow{P_i}\times \overrightarrow{P_{i+1}})
21(Pn×P1 +i=1∑n−1Pi×Pi+1)
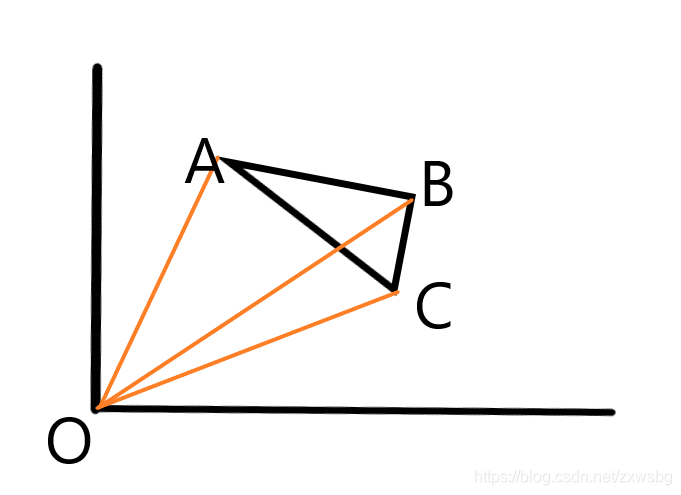
用
S
Δ
O
C
B
+
S
Δ
O
B
A
−
S
Δ
O
A
C
S_{\Delta OCB}+S_{\Delta OBA} - S_{\Delta OAC}
SΔOCB+SΔOBA−SΔOAC
注:OA
×
\times
×OC结果为
−
S
Δ
O
A
C
-S_{\Delta OAC}
−SΔOAC
求两圆的交点与公切线
交点
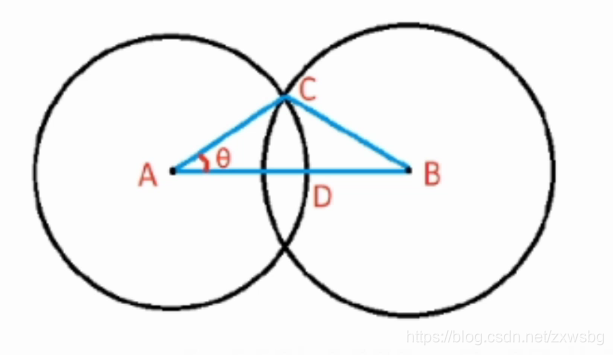
A
C
=
r
1
,
B
C
=
r
2
,
A
B
=
d
AC=r_1,BC=r_2,AB=d
AC=r1,BC=r2,AB=d
- 算 θ \theta θ
- 将D旋转 θ \theta θ
公切线
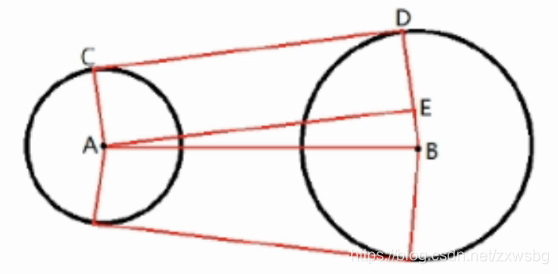
- 用|AB|和|BE|算出 θ \theta θ
- 将F逆时针旋转 90 ° 90\degree 90°,其他同理
凸包
一个点集的凸包就是能包围给定点的最小的凸多边形。
求凸包的方法
按极角序 (Graham扫描法)
要考虑因素较多,这里不介绍
按水平序 (Andrew算法)
- 以横坐标为第一关键字,纵坐标为第二关键字对所有点进行排序;
- 顺序枚举每一个点,如果该点在当前凸包前进方向的左侧则把它加入栈,否则不断退栈知道满足条件。这样就求出了下凸包;
- 倒序枚举,求出上凸包;
- 合并上下凸包,一边用归并排序一边用前面的方法维护当前凸包。
时间复杂度:瓶颈在排序上
注意:一定要按纵坐标排序
常见问题
询问点是否在凸包内
下凸包:二分处这个点在哪两个点之间,然后判断是否在这两个点的线的上面。
上凸包同理。






















 238
238

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










