Sqrt(x) -- leetcode

题目描述：
Implement int sqrt(int x).

Compute and return the square root of x.

如果输入的是正整数，并且，输出int类型的话，可以用二分查找的方法。
对于一个非负数n，它的平方根不会大于（n/2+1）。因为：
$(n/2+1)^2=n+1+n^2/4>n$。因此只需要在[0, n/2+1]的区间内二分查找。
代码：

class Solution {
public:
    int mySqrt(int x) {
        long long low = 0;
        long long high = x / 2 +1;
        long long mid = 0, p = 0;
        while(low <= high){
            mid = (low + high)/2;
            p = mid * mid;
            if (p == x) return mid;
            if (p < x) low = mid+1;
            if (p > x) high = mid-1;
        }
        return high;
    }
};

牛顿法：解决 double 类型的 x。

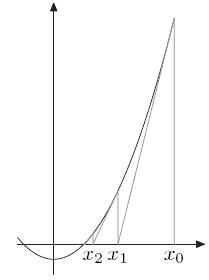
可以将求sqrt（x）转为函数：$f(x) = x^2 - n$的求解。

首先取$x_0$，若 x