一、二分图最大匹配
二分图最大匹配的经典匈牙利算法是由Edmonds在1965年提出的,算法的核心就是根据一个初始匹配不停的找增广路,直到没有增广路为止。
匈牙利算法的本质实际上和基于增广路特性的最大流算法还是相似的,只需要注意两点:(一)每个X节点都最多做一次增广路的起点;(二)如果一个Y节点已经匹配了,那么增广路到这儿的时候唯一的路径是走到Y节点的匹配点(可以回忆最大流算法中的后向边,这个时候后向边是可以增流的)。
找增广路的时候既可以采用dfs也可以采用bfs,两者都可以保证O(nm)的复杂度,因为每找一条增广路的复杂度是O(m),而最多增广n次,dfs在实际实现中更加简短。
二、匈牙利算法
二分图的最大匹配有两种求法,第一种是最大流;第二种就是我现在要讲的匈牙利算法。这个算法说白了就是最大流的算法,但是它跟据二分图匹配这个问题的特点,把最大流算法做了简化,提高了效率。
最大流算法的核心问题就是找增广路径(augment path)。匈牙利算法也不例外,它的基本模式就是:
初始时最大匹配为空
while 找得到增广路径
do 把增广路径加入到最大匹配中去
可见和最大流算法是一样的。但是这里的增广路径就有它一定的特殊性,下面我来分析一下。
(注:匈牙利算法虽然根本上是最大流算法,但是它不需要建网络模型,所以图中不再需要源点和汇点,仅仅是一个二分图。每条边也不需要有方向。)
二分图中的增广路径的性质:
(1)有奇数条边。
(2)起点在二分图的左半边,终点在右半边。
(3)路径上的点一定是一个在左半边,一个在右半边,交替出现。(其实二分图的性质就决定了这一点,因为二分图同一边的点之间没有边相连,不要忘记哦。)
(4)整条路径上没有重复的点。
(5)起点和终点都是目前还没有配对的点,而其它所有点都是已经配好对的。(如图1、图2所示,[1,5]和[2,6]在图1中是两对已经配好对的点;而起点3和终点4目前还没有与其它点配对。)
(6)路径上的所有第奇数条边都不在原匹配中,所有第偶数条边都出现在原匹配中。(如图1、图2所示,原有的匹配是[1,5]和[2,6],这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。)
(7)最后,也是最重要的一条,把增广路径上的所有第奇数条边加入到原匹配中去,并把增广路径中的所有第偶数条边从原匹配中删除(这个操作称为增广路径的取反),则新的匹配数就比原匹配数增加了1个。
对于增广路径还可以用一个递归的方法来描述。这个描述不一定最准确,但是它揭示了寻找增广路径的一般方法:
“从点A出发的增广路径”一定首先连向一个在原匹配中没有与点A配对的点B。如果点B在原匹配中没有与任何点配对,则它就是这条增广路径的终点;反之,如果点B已与点C配对,那么这条增广路径就是从A到B,再从B到C,再加上“从点C出发的增广路径”。并且,这条从C出发的增广路径中不能与前半部分的增广路径有重复的点。
但是要完成匈牙利算法,还需要一个重要的定理:
如果从一个点A出发,没有找到增广路径,那么无论再从别的点出发找到多少增广路径来改变现在的匹配,从A出发都永远找不到增广路径。(给个提示。如果你试图举个反例来说明在找到了别的增广路径并改变了现有的匹配后,从A出发就能找到增广路径。那么,在这种情况下,肯定在找到别的增广路径之前,就能从A出发找到增广路径。这就与假设矛盾了。)
有了这个定理,匈牙利算法就成形了。如下:
初始时最大匹配为空
for 二分图左半边的每个点i
do 从点i出发寻找增广路径。如果找到,则把它取反(即增加了总了匹配数)
如果二分图的左半边一共有n个点,那么最多找n条增广路径。如果图中共有m条边,那么每找一条增广路径(DFS或BFS)时最多把所有边遍历一遍,所花时间也就是m。所以总的时间大概就是O(n * m)。
这是一种用增广路求二分图最大匹配的算法。它由匈牙利数学家Edmonds于1965年提出,因而得名。 定义 未盖点:设Vi是图G的一个顶点,如果Vi 不与任意一条属于匹配M的边相关联,就称Vi 是一个未盖点。
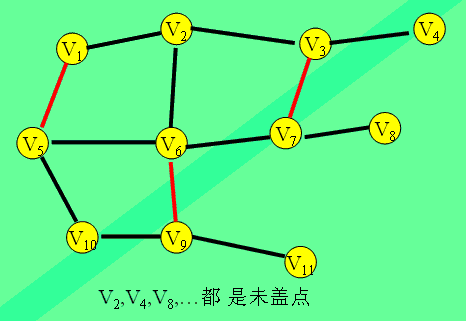
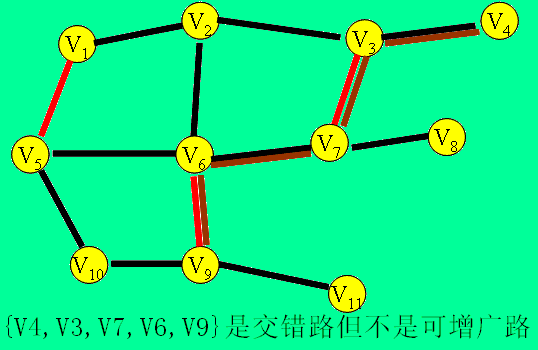
交错路:设P是图G的一条路,如果P的任意两条相邻的边一定是一条属于M而另一条不属于M,就称P是一条交错路。
可增广路:两个端点都是未盖点的交错路叫做可增广路。
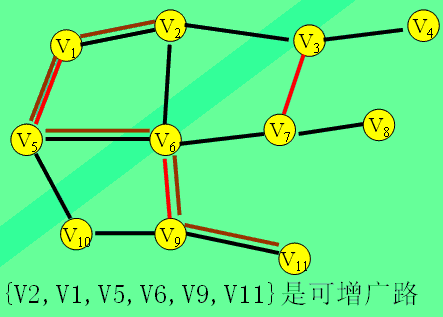
流程图
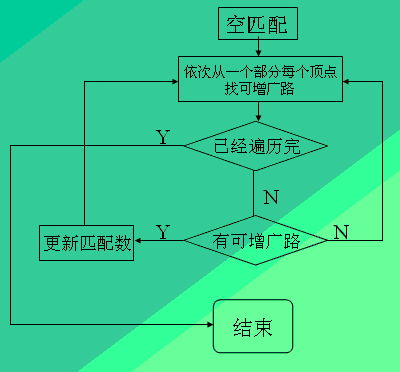
伪代码:
[cpp] view plaincopy
- bool 寻找从k出发的对应项出的可增广路
- {
- while (从邻接表中列举k能关联到顶点j)
- {
- if (j不在增广路上)
- {
- 把j加入增广路;
- if (j是未盖点 或者 从j的对应项出发有可增广路)
- {
- 修改j的对应项为k;
- 则从k的对应项出有可增广路,返回true;
- }
- }
- }
- 则从k的对应项出没有可增广路,返回false;
- }
- void 匈牙利hungary()
- {
- for i->1 to n
- {
- if (则从i的对应项出有可增广路)
- 匹配数++;
- }
- 输出 匹配数;
- }
C实现(作者BYVoid)
[cpp] view plaincopy
- #include <stdio.h>
- #include <string.h>
- #define MAX 102
- long n,n1,match;
- long adjl[MAX][MAX];
- long mat[MAX];
- bool used[MAX];
- FILE *fi,*fo;
- void readfile()
- {
- fi=fopen("flyer.in","r");
- fo=fopen("flyer.out","w");
- fscanf(fi,"%ld%ld",&n,&n1);
- long a,b;
- while (fscanf(fi,"%ld%ld",&a,&b)!=EOF)
- adjl[a][ ++adjl[a][0] ]=b;
- match=0;
- }
- bool crosspath(long k)
- {
- for (long i=1;i<=adjl[k][0];i++)
- {
- long j=adjl[k][i];
- if (!used[j])
- {
- used[j]=true;
- if (mat[j]==0 || crosspath(mat[j]))
- {
- mat[j]=k;
- return true;
- }
- }
- }
- return false;
- }
- void hungary()
- {
- for (long i=1;i<=n1;i++)
- {
- if (crosspath(i))
- match++;
- memset(used,0,sizeof(used));
- }
- }
- void print()
- {
- fprintf(fo,"%ld",match);
- fclose(fi);
- fclose(fo);
- }
- int main()
- {
- readfile();
- hungary();
- print();
- return 0;
- }
先给一个例子
1、起始没有匹配 
2、选中第一个x点找第一跟连线 
3、选中第二个点找第二跟连线 
4、发现x3的第一条边x3y1已经被人占了,找出x3出发的的交错路径x3-y1-x1-y4,把交错路中已在匹配上的边x1y1从匹配中去掉,剩余的边x3y1 x1y4加到匹配中去 
5、同理加入x4,x5。
匈牙利算法可以深度有限或者广度优先,刚才的示例是深度优先,即x3找y1,y1已经有匹配,则找交错路。若是广度优先,应为:x3找y1,y1有匹配,x3找y2。
三、Hopcroft-Karp算法
该算法由John.E.Hopcroft和Richard M.Karp于1973提出,故称Hopcroft-Karp算法。匈牙利算法的复杂度为O(nm),其中n是顶点数。
原理
为了降低时间复杂度,可以在增广匹配集合M时,每次寻找多条增广路径。这样就可以进一步降低时间复杂度,可以证明,算法的时间复杂度可以到达O(n^0.5*m),虽然优化不了多少,但在实际应用时,效果还是很明显的。
该算法的精髓在于同时找多条增广路进行反转。我们先用BFS找出可能的增广路,这里用到BFS层次搜索的概念,记录当前结点在第几层,用于后面DFS沿增广路反转时用,然后再用DFS沿每条增广路反转。这样不停地找,直至无法找到增广路为止。
基本算法
该算法主要是对匈牙利算法的优化,在寻找增广路径的时候同时寻找多条不相交的增广路径,形成极大增广路径集,然后对极大增广路径集进行增广。在寻找增广路径集的每个阶段,找到的增广路径集都具有相同的长度,且随着算法的进行,增广路径的长度不断的扩大。可以证明,最多增广n^0.5次就可以得到最大匹配。
它的思想跟dinic有点像,大概就是每次先广搜出一个距离标号,然后匈牙利的增广过程就只找标号等于自己加一的点,一次标号多次增广。
算法分为若干阶段,每阶段包含若下步骤:
(1)将左侧未匹配点集设为起点,按照交错路径的条件,BFS,对图分层,在某层出现未匹配的右边点时停止
(2)将左侧未匹配点集设为起点,按照层的顺序,和交错路径的条件,DFS
(3)复杂度:
算法分析:(我不理解?)
(1)在二分图 G = (V; E) 中每个阶段的复杂度为 O(
(2)前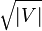
(3)设当前匹配为 M,取的一个最大匹配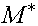
(4)图 G∗ 至多包含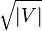
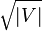
(5)综上,算法最坏复杂度为
伪代码:
[html] view plaincopy
- /*
- G = G1 ∪ G2 ∪ {NIL}
- where G1 and G2 are partition of graph and NIL is a special null vertex
- */
- function BFS ()
- for v in G1
- if Pair_G1[v] == NIL
- Dist[v] = 0
- Enqueue(Q,v)
- else
- Dist[v] = ∞
- Dist[NIL] = ∞
- while Empty(Q) == false
- v = Dequeue(Q)
- if Dist[v] < Dist[NIL]
- for each u in Adj[v]
- if Dist[ Pair_G2[u] ] == ∞
- Dist[ Pair_G2[u] ] = Dist[v] + 1
- Enqueue(Q,Pair_G2[u])
- return Dist[NIL] != ∞
- function DFS (v)
- if v != NIL
- for each u in Adj[v]
- if Dist[ Pair_G2[u] ] == Dist[v] + 1
- if DFS(Pair_G2[u]) == true
- Pair_G2[u] = v
- Pair_G1[v] = u
- return true
- Dist[v] = ∞
- return false
- return true
- function Hopcroft-Karp
- for each v in G
- Pair_G1[v] = NIL
- Pair_G2[v] = NIL
- matching = 0
- while BFS() == true
- for each v in G1
- if Pair_G1[v] == NIL
- if DFS(v) == true
- matching = matching + 1
- return matching
c实作
[cpp] view plaincopy
- //对于要匹配的点 分为x集合的点,和y集合的点
- int Mx[MAX],My[MAX];//那么这里的Mx[i]的值表示x集合中i号点的匹配点,My[j]的值就是y集合j点匹配的点
- int dx[MAX],dy[MAX];//这里就是bfs找增广路用的数组 对于u-->v可达就有dy[v] = dx[u] + 1
- int vis[MAX],dis;//辅助
- bool bfs()
- {
- int i ,v,u;
- dis = INF;
- queue<int>Q;
- memset(dx,-1,sizeof(dx));
- memset(dy,-1,sizeof(dy));
- for(i = 0; i < m ;i ++)//
- if(Mx[i] == -1)
- Q.push(i),dx[i] = 0;
- while(!Q.empty())
- {
- u = Q.front(); Q.pop();
- if(dx[u] > dis) break;
- for(i = head[u]; i != -1; i = edge[i].next)
- {
- v = edge[i].to;
- if(dy[v] == -1)
- {
- dy[v] = dx[u] + 1;
- if(My[v] == -1) dis = dy[v];
- else
- {
- dx[My[v]] = dy[v] + 1;
- Q.push(My[v]);
- }
- }
- }
- }
- return dis != INF;
- }
- bool dfs(int u)
- {
- int v;
- for(int i = head[u]; i != -1; i = edge[i].next)
- {
- v = edge[i].to;
- if(!vis[v] && dy[v] == dx[u] + 1)
- {
- vis[v] = 1;
- if(My[v] != -1 && dy[v] == dis) continue;
- if(My[v] == -1 || dfs(My[v]))
- {
- Mx[u] = v; My[v] = u;
- return true;
- }
- }
- }
- return false;
- }
- int match()
- {
- int ans = 0;
- memset(Mx,-1,sizeof(Mx));
- memset(My,-1,sizeof(My));
- while(bfs())
- {
- memset(vis,0,sizeof(vis));
- for(int u = 0; u < m; u ++)
- if(Mx[u] == -1 && dfs(u))//这里特别要注意,Mx[u] == -1 && dfs(u)先后顺序千万不能换,dfs之后Mx[u]就会变化
- ans ++;
- }
- return ans;
- }
四、KM算法
对于二分图的每条边都有一个权(非负),要求一种完备匹配方案,使得所有匹配边的权和最大,记做最优完备匹配。(特殊的,当所有边的权为1时,就是最大完备匹配问题)
KM算法:(全称是Kuhn-Munkras,是这两个人在1957年提出的,有趣的是,匈牙利算法是在1965年提出的)。
为每个点设立一个顶标Li,先不要去管它的意义。
设vi,j为(i,j)边的权,如果可以求得一个完备匹配,使得每条匹配边vi,j=Li+Lj,其余边vi,j≤Li+Lj。
此时的解就是最优的,因为匹配边的权和=∑Li,其余任意解的权和都不可能比这个大
定理:二分图中所有vi,j=Li+Lj的边构成一个子图G,用匈牙利算法求G中的最大匹配,如果该匹配是完备匹配,则是最优完备匹配。
(不知道怎么证明)
问题是,现在连Li的意义还不清楚。
其实,我们现在要求的就是L的值,使得在该L值下达到最优完备匹配。
L初始化:
Li=max{wi,j}(i∈x,j∈y)
Lj=0
建立子图G,用匈牙利算法求G的最大匹配,如果在某点i (i∈x)找不到增广轨,则得不到完备匹配。
此时需要对L做一些调整:
设S为寻找从i出发的增广轨时访问的x中的点的集合,T为访问的y中的点的集合。
找到一个改进量dx,dx=min{Li+Lj-wi,j}(i∈S,j不∈T)
Li=Li-dx (i∈S)
Li=Li+dx (i∈T)
重复以上过程,不断的调整L,直到求出完备匹配为止。
从调整过程中可以看出:
每次调整后新子图中在包含原子图中所有的边的基础上添加了一些新边。
每次调整后∑Li会减少dx,由于每次dx取最小,所以保证了解的最优性。
复杂度分析:
设m为边数,从x中的一个未盖点出发寻找增广轨的复杂度最坏是O(m),每次调整后至少添加一条边,则最多调整m次,每次调整的的复杂度最坏是O(m),所以总的复杂度在最坏情况下是O(m+m2)=O(m2)
扩展:
根据KM算法的实质,可以求出使得所有匹配边的权和最小的匹配方案。
L初始化:
Li=min{wi,j}(i∈x,j∈y)
Lj=0
dx=min{wi,j-Li-Lj}(i∈S,j不∈T)
Li=Li+dx (i∈S)
Li=Li-dx (i∈T)
【最优匹配】
与最优完备匹配很相似,但不必以完备匹配为前提。
只要对KM算法作一些修改就可以了:
将原图转换成完全二分图(m=|x||y|),添加原图中不存在的边,并且设该边的权值为0。
/*其实在求最大 最小的时候只要用一个模板就行了,把边的权值去相反数即可得到另外一个.求结果的时候再去相反数即可*/
/*最大最小有一些地方不同。。*/
#include <iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
//赤裸裸的模板啊。。
const int maxn = 101;
const int INF = (1<<31)-1;
int w[maxn][maxn];
int lx[maxn],ly[maxn]; //顶标
int linky[maxn];
int visx[maxn],visy[maxn];
int slack[maxn];
int nx,ny;
bool find(int x)
{
visx[x] = true;
for(int y = 0; y < ny; y++)
{
if(visy[y])
continue;
int t = lx[x] + ly[y] - w[x][y];
if(t==0)
{
visy[y] = true;
if(linky[y]==-1 || find(linky[y]))
{
linky[y] = x;
return true; //找到增广轨
}
}
else if(slack[y] > t)
slack[y] = t;
}
return false; //没有找到增广轨(说明顶点x没有对应的匹配,与完备匹配(相等子图的完备匹配)不符)
}
int KM() //返回最优匹配的值
{
int i,j;
memset(linky,-1,sizeof(linky));
memset(ly,0,sizeof(ly));
for(i = 0; i < nx; i++)
for(j = 0,lx[i] = -INF; j < ny; j++)
if(w[i][j] > lx[i])
lx[i] = w[i][j];
for(int x = 0; x < nx; x++)
{
for(i = 0; i < ny; i++)
slack[i] = INF;
while(true)
{
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(find(x)) //找到增广轨,退出
break;
int d = INF;
for(i = 0; i < ny; i++) //没找到,对l做调整(这会增加相等子图的边),重新找
{
if(!visy[i] && d > slack[i])
d = slack[i];
}
for(i = 0; i < nx; i++)
{
if(visx[i])
lx[i] -= d;
}
for(i = 0; i < ny; i++)
{
if(visy[i])
ly[i] += d;
else
slack[i] -= d;
}
}
}
int result = 0;
for(i = 0; i < ny; i++)
if(linky[i]>-1)
result += w[linky[i]][i];
return result;
}
int main()
{
// freopen("g:/1.txt","r",stdin);
while(true)
{
scanf("%d%d",&nx,&ny);
int a,b,c;
while(scanf("%d%d%d",&a,&b,&c),a+b+c)
{
w[a][b]=c;
}
printf("%d\n",KM());
break;
}
return 0;
}
最后欢迎大家访问我的个人网站: 1024s








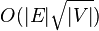
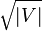
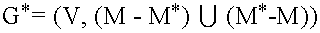
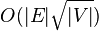














 2346
2346

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








