二叉线索树（Threaded binary tree）

二叉树是一种非线性结构，对二叉树进行遍历时，实际上那个是将二叉树这种非线性结构按某种需要转化成线性序列，但每次遍历二叉树时，都要用递归对其进行遍历，当二叉树的节点较多时，这样的效率是很低的。所以我们有没有办法把我们遍历的二叉树保存，方便以后遍历呢?

在一棵只有n个结点的二叉树中，假设有n个结点，那么就有2n个指针域，因为二叉树只用到了其中的n-1个结点，所以只要利用剩下的n+1个节点，我们就能把中需遍历时所得到的中序二叉树保存下来，以便下次访问。

中序二叉树的指针域有两种类型：一是用于链接二叉树本身；二是用于链接中序遍历序列。这类型的指针，左指指向中序遍历时节点顺序的前驱，右指针指向中序遍历时的后继。为了区别这两种指针域类型，我们在树的结点中要加上两个标志lchild和rchild，分别标志左右指针域的类型。 其数据结构如下：

其中LTag = 0 lchild域指示节点的左孩子；LTag=1 lchild域指示节点的前驱。

RTag = 0 rchild域指示节点的左孩子；RTag=1 rchild域指示节点的前驱。

为了简化二叉树的线索化，这里采用中序线索链表的方式，对二叉树进行遍历，找出叶子节点的前驱和后继。后序后继线索二叉树以后再做讨论。

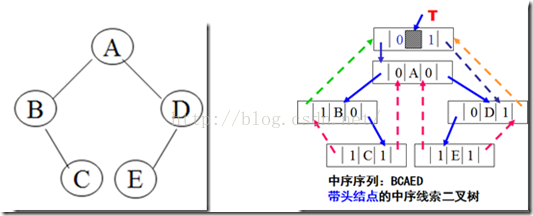
线索二叉树及其中序线索链表结构如下：

为了仿照线性表的存储结构，在二叉树的线索链表上添加一个头结点，令其lchild域指向二叉树的根节点，其rchild域的指针指向中序遍历访问的最后一个节点。反之，令二叉树中序序列中的第一个节点的lchild域指针和最后一个节点的rchild域的指针均指向头结点。

二叉线索树的定义：

TBTreeNode head; // 头结点
TBTreeNode root; // 根节点

在定义二叉树的数据结构后，需要对二叉树遍历进行线索化。

二叉树的线索化(动画演示)

如何进行二叉树的线索化呢？ 由于线索化的是指是将二叉链表中的空指针改为指向前驱和后继的线索，而前驱或后继的信息只有在遍历的时侯才用的到，因此线索化的过程即为在遍历的过程中修改空指针的过程。

创造中序线索树的具体过程: 
递归实现,函数的参数为当前结点current,和上次访问的结点previous. 
(1)若previous的右指针为空,则把previous的右指针指向current,并把previous的RTag设置为true; 
(2)若current的左指针为空,则把current的左指针指向previous,并把current的LTag设置为true;

代码，默认建立的二叉树结构如下：

结点类：

package tree.thread;

public class Node
{
	private int data;
	private Node left;
	private boolean leftIsThread;        // 左孩子是否为线索
	private Node right;
	private boolean rightIsThread;       // 右孩子是否为线索

	public Node(int data)
	{
		this.data = data;
		this.left = null;
		this.leftIsThread = false;
		this.right = null;
		this.rightIsThread = false;
	}

	public int getData()
	{
		return data;
	}

	public void setData(int data)
	{
		this.data = data;
	}

	public Node getLeft()
	{
		return left;
	}

	public void setLeft(Node left)
	{
		this.left = left;
	}

	public boolean isLeftIsThread()
	{
		return leftIsThread;
	}

	public void setLeftIsThread(boolean leftIsThread)
	{
		this.leftIsThread = leftIsThread;
	}

	public Node getRight()
	{
		return right;
	}

	public void setRight(Node right)
	{
		this.right = right;
	}

	public boolean isRightIsThread()
	{
		return rightIsThread;
	}

	public void setRightIsThread(boolean rightIsThread)
	{
		this.rightIsThread = rightIsThread;
	}

	@Override
	public boolean equals(Object obj)
	{
		if (obj instanceof Node)
		{
			Node temp = (Node) obj;
			if (temp.getData() == this.data)
			{
				return true;
			}
		}
		return false;
	}

	@Override
	public int hashCode()
	{
		return super.hashCode() + this.data;
	}
}
</span>

线索二叉树类：

package tree.thread;

public class ThreadTree
{
	private Node root;         // 根节点
	private int size;          // 大小
	private Node pre = null;   // 线索化的时候保存前驱

	public ThreadTree()
	{
		this.root = null;
		this.size = 0;
		this.pre = null;
	}

	public ThreadTree(int[] data)
	{
		this.pre = null;
		this.size = data.length;
		this.root = createTree(data, 1);   // 创建二叉树
	}

	/**
	 * 创建二叉树
	 * 
	 */
	public Node createTree(int[] data, int index)
	{
		if (index > data.length)
		{
			return null;
		}
		Node node = new Node(data[index - 1]);
		Node left = createTree(data, 2 * index);
		Node right = createTree(data, 2 * index + 1);
		node.setLeft(left);
		node.setRight(right);
		return node;
	}

	/**
	 * 将以root为根节点的二叉树线索化
	 * 
	 */
	public void inThread(Node root)
	{
		if (root != null)
		{
			inThread(root.getLeft());     // 线索化左孩子
			if (null == root.getLeft())   // 左孩子为空
			{
				root.setLeftIsThread(true);    // 将左孩子设置为线索
				root.setLeft(pre);
			}
			if (pre != null && null == pre.getRight())  // 右孩子为空
			{
				pre.setRightIsThread(true);
				pre.setRight(root);
			}
			pre = root;
			inThread(root.getRight());       // 线索化右孩子
		}
	}

	/**
	 * 中序遍历线索二叉树
	 * 
	 */
	public void inThreadList(Node root)
	{
		if (root != null)
		{
			while (root != null && !root.isLeftIsThread())    // 如果左孩子不是线索 查找起始结点(中序遍历的开始节点)

			{     
				root = root.getLeft();
			}

			do
			{
				System.out.print(root.getData() + ",");
				if (root.isRightIsThread())   // 如果右孩子是线索，直接获取

				{        
					root = root.getRight();
				} 
				else         // 有右孩子，中序遍历查找右子树中序遍历的第一个节点(即为后继节点)
 
				{      
					root = root.getRight();
					while (root != null && !root.isLeftIsThread())
					{
						root = root.getLeft();
					}
				}
			} while (root != null);
		}
	}

	/**
	 * 前序遍历递归算法
	 * 
	 */
	public void preList(Node root)
	{
		if (root != null)
		{
			System.out.print(root.getData() + ",");
			preList(root.getLeft());
			preList(root.getRight());
		}
	}

	/**
	 * 中序遍历
	 * 
	 */
	public void inList(Node root)
	{
		if (root != null)
		{
			inList(root.getLeft());
			System.out.print(root.getData() + ",");
			inList(root.getRight());
		}
	}

	public Node getRoot()
	{
		return root;
	}

	public void setRoot(Node root)
	{
		this.root = root;
	}

	public int getSize()
	{
		return size;
	}

	public void setSize(int size)
	{
		this.size = size;
	}

}</span>

测试类：

package tree.thread;

public class ThreadTreeTest
{
	public static void main(String[] args)
	{
		int[] data = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
		
		ThreadTree threadTree = new ThreadTree(data);      // 创建普通二叉树
		threadTree.inList(threadTree.getRoot());           // 中序递归遍历二叉树
		System.out.println();

		threadTree.inThread(threadTree.getRoot());         // 采用中序遍历将二叉树线索化
		threadTree.inThreadList(threadTree.getRoot());     // 中序遍历线索化二叉树
	}
}</span>

由于它充分利用了空指针域的空间（等于节省了空间），又保证了创建时的一次遍历就可以终生受用前驱后继的信息（这意味着节省了时间），所以在实际问题中，如果所使用的二叉树需要经常遍历或查找结点时需要某种遍历序列中的前驱和后继，那么采用线索二叉链表的存储结构就是不错的选择；

转载自：http://www.cnblogs.com/ttltry-air/archive/2012/07/10/2584312.html

http://blog.csdn.net/jiangnan2014/article/details/38656803