| ProblemE: Matches |
We can make digits with matches as shown below:

Given N matches, find the number of different numbers representable using the matches. We shall only make numbers greater than or equal to 0, so no negative signs should be used. For instance, if you have 3 matches, then you can only make the numbers 1 or 7. If you have 4 matches, then you can make the numbers 1, 4, 7 or 11. Note that leading zeros are not allowed (e.g. 001, 042, etc. are illegal). Numbers such as 0, 20, 101 etc. are permitted, though.
Input
Input contains no more than 100 lines. Each line contains one integer N (1 ≤ N ≤ 2000).
Output
For each N, output the number of different (non-negative) numbers representable if you have N matches.
Sample Input
3 4
Sample Output
2 4
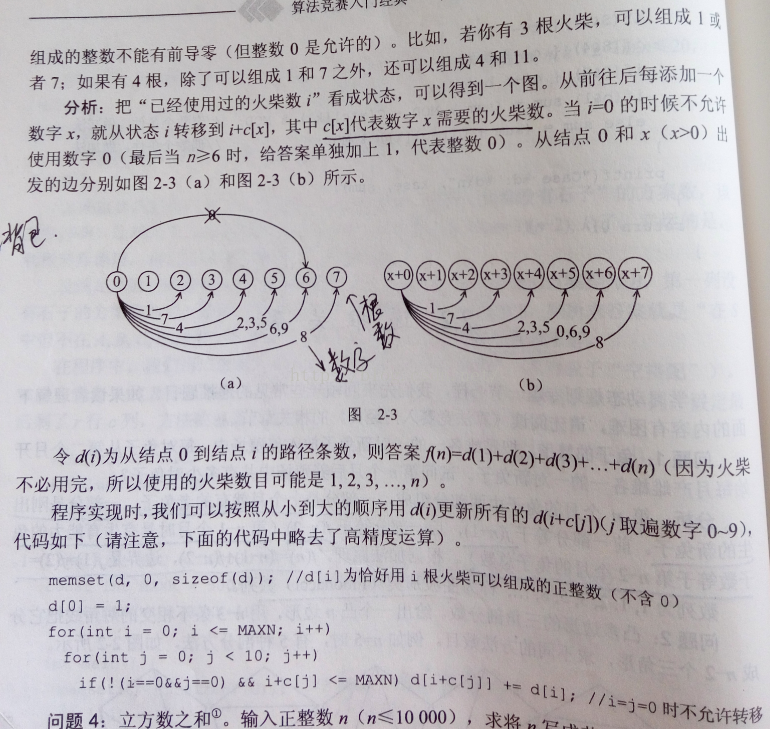
题意:用n根火柴能组成多少个非负整数?火柴不必用完,组成的整数不能有前导零(但整数0是允许的)![]() 。
。
code:
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int MAXN = 2000 + 5;
const int c[15] = {6,2,5,5,4,5,6,3,7,6};
class node
{
public:
node() ///构造函数,将 a 清零,len赋初值为0
{
memset(a, 0, sizeof(a));
len = 0;
}
node(int n) ///重载构造函数
{
a[0] = n;
len = 1;
}
node operator + (const node& b) ///重载 + 运算符,功能使两个类相加
{
len = max(len, b.len);
for(int i = 0; i < len; i++)
{
a[i] += b.a[i];
a[i + 1] += a[i] / 10;
a[i] %= 10;
}
if(a[len]) len++;
return *this;
}
void out() ///输出函数
{
if(len == 0) printf("0");
else
{
for(int i = len - 1; i >= 0; i--)
printf("%d", a[i]);
}
printf("\n");
}
private:
int a[500], len;
} f[MAXN];
int main()
{
f[0] = node(1);
for(int i = 0; i <= MAXN; i++)
for(int j = 0; j < 10; j++)
if(!(i == 0 && j == 0) && i + c[j] <= MAXN) ///i,j不能同时为0
f[i + c[j]] = f[i + c[j]] + f[i];
f[6] = f[6] + node(1);
for(int i = 2; i <= MAXN; i++) f[i] = f[i] + f[i - 1];
int n;
while(~scanf("%d", &n))
f[n].out();
return 0;
}
























 87
87











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








