查找(1) 二叉搜索树

定义和表示

搜索树支持许多动态集合操作，search\minimum\maximum\predecessor(前驱)\successor(后继)\insert\delete等，所以可以把搜索树作为字典或优先队列。
二叉搜索树以一棵二叉树组织的，他需要满足一些条件(性质)。

对于任何结点x, x的左子树的最大关键字不大于x结点的关键字，x的右子树的最小关键字不小于x结点的关键字。
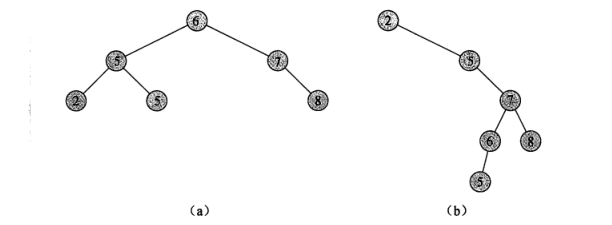
二叉搜索树操作的最坏时间与树高成正比，上图中(a)是一个包含6结点，高度为2的二叉搜索树(也属于平衡树)。而(b)是一个包含相同关键字，高度为4的低效二叉搜索树。

我们用基于链表的形式表达二叉树。

class TreeNode:
    def __init__(self,key=None):
        self.key = key
        self.parent = None
        self.left = None
        self.right = None

class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.nodeNum = 0

    def getRoot(self):
        return self.root

    def getNodeNum(self):
        return self.nodeNum

遍历

中根遍历：依次中根遍历左子树、输出根节点、中根遍历右子树。
先根遍历：依次输出根节点、先根遍历左子树、先根遍历右子树。
后根遍历：依次后根遍历左子树、后根遍历右子树、输出根节点。
层级遍历：从上到下，从左至右，从根到叶结点的依序遍历。
二叉树遍历的代码如下：

    #中根遍历递归版
    def inOrderRec(self,r):
        if r:
            self.inOrderRec(r.left)
            print(r.key,end=' ')
            self.inOrderRec(r.right)

    #中根遍历非递归版，借用栈       
    def inOrderWithStack(self):
        s = Stack()
        r = self.getRoot()
        while r or not s.isEmpty():
            if r:
                s.push(r)
                r = r.left
            else:
                r = s.pop()
                print(r.key,end = ' ')
                r = r.right

    #中根遍历非递归非栈版，Joseph M.Morris实现。主要思想利用线索二叉树
    #利用所有叶子结点的右指针，指向其后继结点，组成一个环，
    #在第二次遍历到这个结点时，由于其左子树已经遍历完了，则访问该结点。
    def inOrderNoRecNoStack(self):
        p = self.getRoot()
        r = None
        while p:
            q = p.left
            if q:
                while q is not r and q.right:
                    q = q.right
                if q is not r:
                    q.right = p
                    p = p.left
                    continue
                else:
                    q.right = None
            print(p.key,end=' ')
            r = p
            p = p.right

    #中根遍历非递归版，借用后继，该版本使用到了父指针进行回溯。
    def inOrder(self):
        r = self.getRoot()
        p = self.minMum(r)
        while p:
            print(p.key,end= ' ')
            p = self.successor(p)

    #先根遍历递归版
    def preOrderRec(self,r):
        if r:
            print(r.key,end=' ')
            self.preOrderRec(r.left)
            self.preOrderRec(r.right)

    #后根遍历递归版    
    def postOrderRec(self,r):
        if r:
            self.postOrderRec(r.left)
            self.postOrderRec(r.right)
            print(r.key,end=' ')

    #层级遍历，借用队列  
    def levelOrder(self):
        q = Queue()
        p = self.getRoot()
        while p:
            print(p.key, end=' ')
            if p.left:
                q.enqueue(p.left)
            if p.right:
                q.enqueue(p.right)
            if q.isEmpty():
                p = None
            else:
                p = q.dequeue()

查询

二叉搜索树的查询操作包括：search查找、minimum最小关键字和maximum最大关键字、predecessor前驱、successor后继。这里主要说一下怎么找出后继和前驱。其他的都很简单。

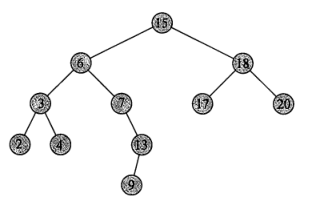
由上图举例，找出结点i的后继分两种情况：
①：如果i结点有右子树，那么i结点的后继就是i结点的右子树的最小关键字结点。比如15的后继是17，7的后继是9，等等。
②：如果i结点没有右子树，那么需要从i开始沿树而上直到遇到这样一个结点，该结点是其父结点的左孩子，那这个父结点就是i的后继。请仔细体会这个过程。
比如，根据上图给出要查找13的后继的过程。13的父结点是7，但是13不是7的左孩子，继续向上搜索，7的父结点是6，但是7不是6的左孩子，继续向上搜索，6的父结点是15,并且6是15的左孩子，结点15就是13的后继。
至于前驱的查找是后继查找的一种对称情况。

上述操作代码实现如下：

    def search(self,key):
        p = self.getRoot()
        while p and key is not p.key:
            if key < p.key:
                p = p.left
            else:
                p = p.right
        return p

    def minMum(self,p):
        while p.left:
            p = p.left
        return p

    def maxMum(self,p):
        while p.right:
            p = p.right
        return p

    def successor(self,p):
        if p.right:
            return self.minMum(p.right)
        x = p.parent
        while x and p is x.right:
            p = x
            x = x.parent
        return x

    def predecessor(self,p):
        if p.left:
            return self.maxMum(p.left)
        x = p.parent
        while x and p is x.left:
            p = x
            x = x.parent
        return x

插入和构建

对于插入一个结点来说，首先找到插入的合适位置，能保证二叉搜索树的性质。

    def insert(self,key):
        node = TreeNode(key)
        x = None
        p = self.getRoot()
        while p:
            x = p
            if node.key < p.key:
                p = p.left
            else:
                p = p.right
        node.parent = x
        if not x:
            self.root = node
        elif node.key < x.key:
            x.left = node
        else:
            x.right = node
        self.nodeNum += 1

有了插入操作，构建二叉树的代码就简单多了。

    #datalist = [key1,key2,...,keyn]
    def build(self,datalist):
        for key in datalist:
            self.insert(key)

删除

相对于插入操作，二叉搜索树的删除操作稍微复杂点。
以p为将要删除的结点分三种情况来具体说明：
①：p没有左孩子，用p的右孩子去代替p。这里其实包括了p有右孩子和p没有右孩子两种情况，用p的右孩子去代替p对于两种情况都是符合要求的。
②：p没有右孩子，即这种情况下，p有且仅有左孩子，把p的左孩子去代替p即可。
③：p有左孩子也有右孩子，找到p的后继psu(一定有)，psu的关键字和卫星数据(如果有)复制给p，然后把问题转化为删除psu结点，而根据性质，psu一定没有左孩子，那又回到了情况①，按照①的处理方式即可。
这里有个关键点是结点替换过程。我们将其封装定义为_transplant子过程。

    #结点替换，v结点替换p结点
    def _transplant(self,p,v):
        if not p.parent:
            self.root = v
        elif p is p.parent.left:
            p.parent.left = v
        else:
            p.parent.right = v
        if v:
            v.parent = p.parent

    def delete(self,key):
        p = self.search(key) #找到所要删除的关键字的结点，可能没有
        if p:
            if not p.left: #case 1
                self._transplant(p, p.right)
            elif not p.right: #case 2
                self._transplant(p, p.left)
            else: #case 3
                x = self.minMum(p.right) #x是p的后继    
                p.key = x.key
                self._transplant(x, x.right) #问题退化到case 1 
            self.nodeNum -= 1

二叉搜索树上的每个基本操作都能在O(h)内完成，h为树的高度。在构建二叉搜索树的最坏情况下，树可能退化成单链，那操作的代价就会大大增加。~

---