首先着重来讲一下什么叫“没装满”?
以一个例子说明:
1 w[1]=2 v[1]=1
2 w[2]=3 v[2]=2
3 w[3]=5 v[3]=3
设目标承重W=4
填表如下:
0 1 2 3 4 (w)
i=0 0 0 0 0 0
1 0 0 1 1 1
2 0 0 1 2 2
3 0 0 1 2 2
怎样判断是不是装满了呢?
i=2和i=3,对应的f值相等,说明第三件物品必然没有放进背包;i=1和i=2,对应的f值不等,说明第二件物品放进了背包。再往前找,i=2时,w=3和w=4对应的f值相等,说明背包必然是没有装满的!空出的体积为4-3=1.
也可以这么看,f[4]=2,说明装的是w[2]=3,3<4,必然没有装满。
为什么会出现这种情况呢?i=2时,f [4] = max { f [4] , f [ 4-w[2] ]+ v[2] } = 2
f [ 4-w[2] ]+ v[2]表示第二阶段要放入w[2],但f[4-w[2]]=f[1]=0,说明f[1]时没有放入任何物品(放不下),所以即便放入w[2]怎么可能使承重为4的背包满呢!?
总结:我们可以保证f[ j- w[i] ]+v[i] 表示我们会且能(不能就是上一阶段的 f[j] )放入 w[i]的物品,但因为不能保证状态为j-w[i]时背包本身就是满的,所以也不能保证放入 w[i] 后承重为 j 的背包能装满!
注:
1)f[ w[i] ] = f [ 0 ]+ v[i] 表示只放了物品i,f[ 2*w[i] ] = f [ w[i] ]+ v[i] 表示在已放一件物品i的基础上再放一件物品 i 。f[ 2*w[i]-1 ] = f [ w[i]-1 ]+ v[i] 表示在原承重为w[i]-1 的背包中(至于具体放了什么、结果如何我们不关心)放入物品i使得新的承重为2*w[i]-1 (这是放不下两件物品i的)。
2)每个位置j都有且仅有一个值,不好的(没添加第i件物品的)状态总会被更好(添加了第i件物品的)的状态替换掉。
3)由此,可以这样通俗的理解什么叫没装满。背包目标承重为5,到最后一阶段最后一状态(或任意一阶段任意一状态)比如w[3]=3,为了能放下w[3]必须要先从背包中(目前的背包处于此阶段的前一阶段,可能有w[1]和w[2]中的一个或几个)拿出重量为3的物品,使得背包有余量放下第i个物品,此时背包中只剩下一个重量为2的物品,但如果w[1]和w[2]都不等于2,那么此时背包的余量必然是大于3的(小于2的填不满,大于2的放不进),放进w[3]之后背包仍留有余量(如果上一阶段的最后一个状态比此时的状态好,就保留上次的状态而不会被替换)
一、小题热身
Description:
话说月光家里有许多玩具,最近他又看上了DK新买的“擎天柱”,就想用自己的跟DK的换。每种玩具都有特定的价格,价格为整数。只有月光拿出的玩具的总价格与“擎天柱”的价格相等才能换得“擎天柱”。同时,月光还希望能用最少的玩具数换回“擎天柱”。请问,月光能顺利得到梦寐以求的“擎天柱”吗?Input:
输入数据包含多组;对于每组数据,第一行为一个正整数n(1 ≤n≤10); 表示月光手头有n个玩具。接下来一行有n个正整数P1,P2,……,Pn(1 ≤ Pi ≤ 1000),Pi为第i个玩具的所对应的价格。最后一行为一个正整数m(1 ≤ m ≤10000),为“擎天柱”的价格。
Output:
对于每组数据,如果能换得“擎天柱”则输出最少玩具数;否则,输出“-1”。
Sample Input:
3
1 2 3
4
4
4 3 3 5
2
2
-1
解析:很简单的一道动态规划的题目,也可以理解为背包问题,和硬币选取和钢筋截取的题目类似。
直接上状态转移方程:
其中,i 表示当前价值,f [i] 表示当前价值对应的最少玩具数量,v[j] 为第 j 件玩具的价值。
就是这么简单!
二、完全背包
由背包思想很容易得到状态转移方程:
时间复杂度略高,可以优化,
设F[i][j]表示在前 i 种物品中选取若干件物品放入容量为j的背包所得的最大价值。那么对于第i种物品的出现,我们对第 i 种物品放不放入背包进行决策。如果不放那么F[i][j]=F[i-1][j];如果确定放,背包中应该出现至少一件第i种物品,所以F[i][j]种至少应该出现一件第i种物品,即F[i][j]=F[i][j-C[i]]+W[i]。为什么会是F[i][j-C[i]]+W[i]?因为F[i][j-C[i]]里面可能有第i种物品,也可能没有第i种物品。我们要确保F[i][j]至少有一件第i件物品,所以要预留C[i]的空间来存放一件第i种物品。
0-1背包只能由上一阶段的状态转移而来(因为必须确保每件物品最多只放了一次——第i-1阶段是没有第i件物品的,它只能在第i 阶段被放(or 不放)),而完全背包却可能由本阶段状态转移而来,本阶段就意味着第i种物品是允许已经被放过了的!第i阶段j状态是完全可以由第i阶段j-C[i]状态转移而来的,因此v是顺序循环(而非0-1背包的逆序)。
第i阶段每个不同的j值(状态)对应可以放置的第i种物品不同的个数!
状态方程为:
所以区别于0-1背包,伪代码如下:
for i=1...N
for v=c[i]...V
f[v]=max{f[v],f[v-c[i]]+w[i]};
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1248
注意:本题是减去价值(因为加上的是第i种物品的价值),(函数外)再加上价值(因为求得就是价值 f[i][j] )——参数同为第 i 种物品的价值。
三、多重背包
1)二进制思想
问题描述:
假设有1000个苹果,现在要取n个苹果,如何取?正常的做法应该是将苹果一个一个拿出来,直到n个苹果被取出来。
又假设有1000个苹果和10只箱子,如何快速的取出n个苹果呢?可以在每个箱子中放 2^i (i<=0<=n)个苹果,也就是 1、2、4、8、16、32、64、128、256、489(最后的余数),相当于把十进制的数用二进制来表示,取任意n个苹果时,只要推出几只箱子就可以了。
多重背包的拆分(分组,分堆!)思想就是由此演变而来:将第 i 种物品分成若干件物品,其中每件物品有一个系数,这件物品的费用和价值 等于 原来(单个第 i 种物品)的费用和价值乘以这个系数。使这些系数分别为1,2,4,... ,2^(k-1),n[i] - (2^k-1),且k是满足n[i]-(2^k-1)>0的最大整数。分成的这几件物品的系数和为n[i](1+2+4+8+...+2^(k-1)+n[i]-(2^k-1) = n[i]),表明不可能取多于n[i]件的第i种物品。
这种方法也能保证对于0..n[i] 间的每一个整数,均可以用若干个系数的和表示(这就是二进制拆分来解决多重背包问题的原因)。
例如,如果n[i]为13,就将这种物品分成系数分别为1、2、4、6(余数)的四件物品。
处理多重背包问题有两种套路:先拆后0-1背包,边拆边0-1背包,下面是第一种:
#include <iostream>
using namespace std;
int f[201];
int weight[50]; /* 记录拆分后物体重量 */
int value[50]; /* 记录拆分后物体价值 */
int V, N; /* 目标承重和物品种类数 */
void main()
{
int i, j;
scanf("%d %d",&V, &N);
int weig, val, num;
int count = 0;
for(i = 0; i < N; ++i)
{
scanf("%d %d %d",&weig,&val,&num);
for(j = 1; j <= num; j <= 1) // 二进制拆分,最后一个分号是左移一位(相当于乘以2)
{
weight[count] = j * weig;
value[count] = j * val;
count++;
num -= j; //j是被分出去了的,当然要剪掉
}
if(num > 0) //处理(每种物品的)余数
{
weight[count] = num * weig;
value[count] = num * val;
count++;
}
} //把所有的物品全部拆分分组后再统一使用0-1背包
for(i = 0; i < count; ++i) // 使用0-1背包,拆分过后相当于有count个物品
{
for(j = V; j >= weight[i]; --j)
{
f[j] = f[j] > (f[j-weight[i]] + value[i]) ? maxV[j] : (f[j-weight[i]] + value[i]);
}
}
printf("%d",f[V]);
}
下面是 边拆边用0-1背包,问题http://acm.hdu.edu.cn/showproblem.php?pid=2191:
#include <stdio.h>
#include <stdlib.h>
int V; //背包的体积
const int MAX = 10010;
int f[MAX]; //MAX要比背包的体积大
int p[MAX], h[MAX], c[MAX];
void ZeroOnePack (int cost, int weight) //0-1背包
{
int v;
for (v = V; v >= cost; v--)
f[v] = f[v] > (f[v - cost] + weight) ? f[v] : (f[v - cost] + weight);
}
void CompletePack (int cost, int weight) //完全背包
{
int v;
for (v = cost; v <= V; v++)
f[v] = f[v] > (f[v - cost] + weight) ? f[v] : (f[v - cost] + weight);
}
void MultiplePack(int cost, int weight, int amount) //多重背包
{
//完全背包:该类物品原则上是无限供应,
//此时满足条件cost * amount >= V时,
//表示无限量供应,直到背包放不下为止。
if (cost * amount >= V)
CompletePack (cost, weight);
int k = 1;
while (k < amount)
{
ZeroOnePack (k * cost, k * weight); //每拆一次就用一次0-1背包
amount = amount - k;
k = k * 2;
}
if(amount!=0) ZeroOnePack (amount * cost, amount * weight); //剩下的余数也要用一次0-1背包
}
int main(void)
{
int t,i,m;
scanf("%d",&t);
while(t--)
{
scanf("%d %d",&V,&m);
for(i=0;i<=V;i++) //没有要求把背包装满
{
f[i]=0;
}
for(i=1;i<=m;i++)
scanf("%d %d %d",&p[i],&h[i],&c[i]);
for(i=1;i<=m;i++)
MultiplePack(p[i], h[i], c[i]);
printf("%d\n",f[V]);
}
return 0;
}2) 既然有二进制思想,也必然有3进制、4进制...思想
看一道腾讯面试题:一个商人到市场上买钻石,这批钻石的质量都是41g以下,但是商人只有四个砝码,请问他该带哪四个砝码?
这跟上面的二进制思想异曲同工。计算机语言描述为用4位表示最大40的数,很显然三进制数1111满足条件,所以应该带的砝码是1g,3g,9g,27g的。
总结:对于0-1背包和完全背包使用一维数组实现是最简便高效的;对于多重背包,最好是输入时进行二进制拆分,然后使用0-1背包,这样比基本实现和在运算时再进行拆分要简捷的多。










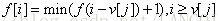
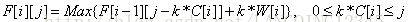
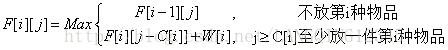













 559
559











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








