初等数论_4 2016.4.4

三、素数（质数）

3.1

素数，有无限个
除了1和它本身以外不再有其他的除数整除

非素数称为合数

根据算术基本定理
每一个比1大的整数，要么本身是一个质数，要么可以写成一系列质数的乘积，最小的质数是2

基本判断思路：
在一般领域，对正整数n
如果用2到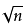之间的所有整数去除，均无法整除，则n为质数

质数大于等于2且不能被它本身和1以外的数整除

3.2、素数的 Eratosthenes（埃拉托色尼）筛法

筛素数法可以比枚举法节约极大量的时间

定n为所求最大值，m为<=n的质数个数

那么枚举需要O(n^2)的时间复杂度

而筛素数法为O(m*n)
显然m远小于n
所以时间效率有很大提升

如1000000的数据范围，用筛素数法可在2s内解决

该算法适用于较小的maxn
对于较大的maxn，内存无法开如此大的空间

思路：
建立一个bool型数组M
若已知一个数M[k]是质数
那么其i（i为正整数）倍M[k*i]必然为合数，可将其去除

HDU 2161 Primes

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 16000 + 5;
bool IsPrime[maxn];

void Init(void);

int main()
{
//    freopen("in.txt", "r", stdin);
    int num = 0;
    int n;
    Init();

    while (cin>>n && n>0) {
        ++num;
        if (IsPrime[n]) {
            printf("%d: yes\n", num);
        } else {
            printf("%d: no\n", num);
        }
    }
    return 0;
}

void Init(void)
{
    memset(IsPrime, true, sizeof(IsPrime));
    IsPrime[1] = false;
    for (int i=2; i*i<=maxn; ++i) {
        if (IsPrime[i]) {
            int j = 2;
            while (i*j <= maxn) {
                IsPrime[i*j] = false;
                ++j;
            }
        }
    }
    IsPrime[2] = false;
}

HDU 2136 Largest prime factor

题意：
求n的最大素因子在素数表中的位置

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 1000000 + 5;
int ans[maxn];

void Init(void);

int main()
{
//    freopen("in.txt", "r", stdin);
    int n;
    Init();

    while (scanf("%d", &n) != EOF) {
        printf("%d\n", ans[n]);
    }
    return 0;
}

void Init(void)
{
    memset(ans, 0, sizeof(ans));
    int Count = 1;
    for (int i=2; i<=maxn; ++i) {
        if (ans[i] == 0) {
            int j = 1;
            while (i*j <= maxn) {
                ans[i*j] = Count;
                ++j;
            }
            ++Count;
        }
    }
}

HDU 2138 How many prime numbers

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <cmath>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;

const double eps = 1e-8;
const int INF = 0x7fffffff;
const int maxn = 70000;
int Prime[maxn];
bool vis[maxn];
int Count = 0;

void Init(void);


int main()
{
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
#endif // __AiR_H
    Init();
    int N;
    while (scanf("%d", &N) != EOF) {
        int num;
        int Count = 0;
        while (N--) {
            scanf("%d", &num);
            bool flag = true;
            int t = sqrt(num) + 1;
            for (int i = 0; Prime[i] < t; ++i) {
                if (num % Prime[i] == 0) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                ++Count;
            }
        }
        printf("%d\n", Count);
    }
    return 0;
}

void Init(void)
{
    memset(vis, false, sizeof(vis));
    for (int i = 2; i < maxn; ++i) {
        if (!vis[i]) {
            vis[i] = true;
            Prime[Count] = i;
            ++Count;
            int j = 2;
            while (1) {
                if (i*j >= maxn) {
                    break;
                } else {
                    vis[i*j] = true;
                    ++j;
                }
            }
        }
    }
}

3.3、区间素数

获得[L , U]区间的素数
L和U很大，但是U-L不是很大

首先线性筛出1到 sqrt(2147483647) 之间所有的素数
然后再通过这些素数筛出给定区间的合数

POJ 2689 Prime Distance

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;

const int maxn = 46340 + 10;
int Prime[maxn];
bool vis[maxn];
int Count = 0;
bool Range[1000005];
int L, U;

void Init(void);
void Filter(void);

int main()
{
//    freopen("in.txt", "r", stdin);
    Init();

    while (cin>>L>>U) {
        memset(Range, true, sizeof(Range));
        Filter();
        if (L == 1) {
            Range[0] = false;
        }
        int Max = 0, Min = 1000005;
        int Max1, Max2, Min1, Min2;
        int p1 = 0, p2 = 0;
        for (int i=0; i<=U-L; ++i) {
            if (Range[i]) {
                if (p1 > 0) {
                    p2 = i+L;
                    int t = p2 - p1;
                    if (t < Min) {
                        Min = t;
                        Min1 = p1;
                        Min2 = p2;
                    }
                    if (t > Max) {
                        Max = t;
                        Max1 = p1;
                        Max2 = p2;
                    }
                    p1 = p2;
                } else {
                    p1 = i+L;
                }
            }
        }
        if (Max == 0) {
            cout<<"There are no adjacent primes."<<endl;
        } else {
            printf("%d,%d are closest, %d,%d are most distant.\n", Min1, Min2, Max1, Max2);
        }
    }
    return 0;
}

void Init(void)
{
    memset(vis, false, sizeof(vis));
    for (int i=2; i<=maxn; ++i) {
        if (!vis[i]) {
            Prime[Count] = i;
            ++Count;
            int j = 2;
            while (i*j <= maxn) {
                vis[i*j] = true;
                ++j;
            }
        }
    }
}

void Filter(void)
{
    for (int i=0; i<Count; ++i) {
        int low = (L-1)/Prime[i] + 1;
        int high = U/Prime[i];
        for (int j=low; j<=high; ++j) {
            if (j > 1) {
                Range[j*Prime[i]-L] = false;
            }
        }
    }
}

3.4、费马素性检验（Fermat primality test）

费马小定理 (Fermat Theory)：

“威尔逊定理、欧拉定理（数论中的欧拉定理）、中国剩余定理(又称孙子定理)、费马小定理并称初等数论四大定理”

对于质数p和任意整数a，有a^p ≡ a(mod p)
反之，若满足a^p ≡ a(mod p)，p也有很大概率为质数
将两边同时约去一个a，则有a^(p-1) ≡ 1(mod p)

也即是说：
假设我们要测试n是否为质数
我们可以随机选取一个数a
然后计算a^(n-1) mod n
如果结果不为1，我们可以100%断定n不是质数

否则我们再随机选取一个新的数a进行测试
如此反复多次，如果每次结果都是1，我们就假定n是质数

该测试被称为Fermat测试

需要注意的是：
Fermat测试不一定是准确的，有可能出现把合数误判为质数的情况

HDU 1098 Ignatius’s puzzle

题意：
方程f(x)=5 * x^13 + 13 * x^5 + k * a * x
输入任意一个数k，是否存在一个数a，对任意x都能使得f(x)能被65整除

解题思路（费马小定理+扩展欧几里德）：
f(x) = 5 * x^13 + 13 * x^5 + k * a * x = x(5 * x^12 + 13 * x^4 + k * a)

因为x可以取任意值，那么必须是 65 | (5*x^12 + 13 * x^4 + k * a)
那么就是说 x^12 / 13 + x^4 / 5 + k * a / 65 正好是一个整数

=> 65 | (k*a)
=> 5 * t1 + 13 * t2 = k * a
=> k * a /65 = t1/13 + t2/5

=> 13 |（x^12+t1 )
=> 5 | (x^4+t2)

13，5均是素数
根据费马小定理可得
x^12 ≡ 1 (mod 13)
x^4 ≡ 1 (mod 5)

=> t1 = 12 + 13*k1
=> t2 = 4 + 5*k2

将t1，t2带入5 * t1 + 13 * t2 = k * a
=> 5 * (12 + 13 * k1) + 13 * (4 + 5 * k2) = k * a
=> 65（k1+k2)+112 = k * a

k已知，设b = k1 + k2
得 k * a + 65 * b = 112

然后用扩展欧几里得算法求解

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;

typedef long long LL;

LL x, y;

LL Ext_Gcd(LL a, LL b, LL &x, LL &y);

int main()
{
//    freopen("in.txt", "r", stdin);
    int k;

    while (cin>>k) {
        LL d = Ext_Gcd(k, 65, x, y);
        if (112%d != 0) {
            cout<<"no"<<endl;
        } else {
            x = (112/d * x % 65 + 65) % 65;
            cout<<x<<endl;
        }
    }
    return 0;
}

LL Ext_Gcd(LL a, LL b, LL &x, LL &y)
{
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    LL d = Ext_Gcd(b, a%b, x, y);
    LL t = x;
    x = y;
    y = t - a/b*y;
    return d;
}

3.6、Miller-Rabin（米勒拉宾）质数测试算法（Miller–Rabin primality test）

Miller和Rabin在Fermat测试上，建立了Miller-Rabin质数测试算法

与Fermat测试相比，增加了一个
二次探测定理：
如果p是一个素数，x是小于p的正整数，且x^2≡1(mod p)
那么要么x=1，要么x=p-1。

这是显然的，因为x^2≡1(mod p)相当于p能整除(x^2 - 1)
也即p能整除(x+1)(x-1)

由于p是素数
那么只可能是x-1能被p整除(此时x=1) 或 x+1能被p整除(此时x=p-1)。

hiho一下 第九十二周

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>

using namespace std;

typedef long long LL;

const int times = 10;   //伪素数测试次数，算法出错概率<=4^(-times)，一般8~10就够了

LL mult_mod(LL a, LL b, LL mod_val);
LL pow_mod(LL x, LL n, LL mod_val);
bool Is_Composite(LL a, LL n, LL x, LL t);
bool Miller_Rabin(LL n);

int main()
{
//    freopen("in.txt", "r", stdin);
    int T;

    cin>>T;
    while (T--) {
        LL n;
        cin>>n;
        if(Miller_Rabin(n)) {
            cout<<"Yes"<<endl;
        } else {
            cout<<"No"<<endl;
        }
    }
    return 0;
}

// 计算ret = (a*b)%mod_val (a, b, mod_val < 2^63)
LL mult_mod(LL a, LL b, LL mod_val)
{
    a %= mod_val;
    b %= mod_val;
    LL ret = 0;
    LL t = a;
    while (b) {
        if (b&1) {
            ret += t;
            if (ret > mod_val) {
                ret -= mod_val;//直接取模慢很多
            }
        }
        t <<= 1;
        if (t > mod_val) {
            t -= mod_val;
        }
        b >>= 1;
    }
    return ret;
}

// 计算 ret = (x^n)%mod_val
LL pow_mod(LL x, LL n, LL mod_val)
{
    LL ret = 1;
    LL t = x%mod_val;
    while (n)
    {
        if (n&1) {
            ret = mult_mod(ret, t, mod_val);
        }
        t = mult_mod(t, t, mod_val);
        n >>= 1;
    }
    return ret;
}

// 通过 a^(n-1)=1(mod n)来判断n是不是素数
// n-1 = x*2^t 中间使用二次判断
// 是合数返回true, 不一定是合数返回false
bool Is_Composite(LL a, LL n, LL x, LL t)
{
    LL ret = pow_mod(a, x, n);
    LL last = ret;
    for(int i=0; i<t; ++i) {
        ret = mult_mod(ret,ret,n);
        if(ret == 1 && last != 1 && last != n-1) {
            return true;
        }
        last = ret;
    }
    if(ret != 1) {
        return true;
    } else {
        return false;
    }
}

//**************************************************
// Miller_Rabin算法
// 是素数返回true,(可能是伪素数)
// 不是素数返回false
//**************************************************
bool Miller_Rabin(LL n)
{
    if(n == 2) {
        return true;
    }
    if(n == 1 || n%2 == 0) {
        return false;
    }
    LL x = n - 1;
    LL t = 0;
    while(x%2 == 0) {
        x /= 2;
        t++;
    }
    srand(time(NULL));
    for(int i=0; i<times; ++i) {
        LL a = rand()%(n-1) + 1;
        if(Is_Composite(a, n, x, t)) {
            return false;
        }
    }
    return true;
}

POJ 3641 Pseudoprime numbers

题意：
两个数如果p是素数输出no
如果p不是素数，判断a^p%p==a是否成立，如果成立输出yes,否则输出no

#include <iostream>
#include <cstdio>

using namespace std;

typedef long long LL;

LL mult_mod(LL a, LL b, LL mod_val);
LL pow_mod(LL x, LL n, LL mod_val);
bool Is_Prime(LL n);

int main()
{
//    freopen("in.txt", "r", stdin);
    LL p, a;

    while (cin>>p>>a && !(p == 0 && a == 0)) {
        if(!Is_Prime(p) && (pow_mod(a, p, p) == a)) {
            cout<<"yes"<<endl;
        } else {
            cout<<"no"<<endl;
        }
    }
    return 0;
}

// 计算ret = (a*b)%mod_val (a, b, mod_val < 2^63)
LL mult_mod(LL a, LL b, LL mod_val)
{
    a %= mod_val;
    b %= mod_val;
    LL ret = 0;
    LL t = a;
    while (b) {
        if (b&1) {
            ret += t;
            if (ret > mod_val) {
                ret -= mod_val;//直接取模慢很多
            }
        }
        t <<= 1;
        if (t > mod_val) {
            t -= mod_val;
        }
        b >>= 1;
    }
    return ret;
}

// 计算 ret = (x^n)%mod_val
LL pow_mod(LL x, LL n, LL mod_val)
{
    LL ret = 1;
    LL t = x%mod_val;
    while (n)
    {
        if (n&1) {
            ret = mult_mod(ret, t, mod_val);
        }
        t = mult_mod(t, t, mod_val);
        n >>= 1;
    }
    return ret;
}

bool Is_Prime(LL n)
{
    for (int i=2; i*i<=n; ++i) {
        if (n%i == 0) {
            return false;
        }
    }
    return true;
}