题目:
做法:
欧拉降幂:
ax≡ax mod ϕ(p)+ϕ(p)(mod p) (x≥p)
证明贴个地址:地址虽然似乎是爬虫搞出来的但是再也找不到了原出处了.
有了欧拉降幂,可以设
f(p)=2222... mod p
带入欧拉降幂:
f(p)=222...modϕ(p)+ϕ(p)mod p
因为2222...≥p显然成立
注意到现在的指数和 f 有相同的结构,即:
由此我们可以递归计算 f ,并将
时间复杂度似乎并不显然,但是注意到递归次数就是使得 ϕ(ϕ(ϕ(...ϕ(p))))=1 的迭代次数.
而有以下结论:
若p是偶数,则ϕ(p)≤p2−12=p2
若p是奇数,则设p的质因子为qi,所以ϕ(p)=pq1−1q1q2−1q2...qn−1qn.注意到p是奇数,则qi为奇数,则qi−1为偶数,故ϕ(p)为偶数,转化为上一个情况
所以,每两次递归调用时 p 至少减半,即调用次数为
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
namespace MYS
{
const int MAXN = 10000005;
typedef long long LL;
int phi_table[MAXN];
int phi(int x)
{
if(phi_table[x]) return phi_table[x];
int &ret = phi_table[x], upper = sqrt(x + 0.5);
ret = x;
for(int i=2;i<=upper;i++) {
if(x % i == 0) {
ret /= i;
ret *= i-1;
while(x % i == 0) x /= i;
}
}
if(x > 1) { ret /= x; ret *= x-1; }
return ret;
}
LL qpow(LL a, LL n, int p)
{
LL ret = 1, tmp = a % p;
while(n) {
if(n & 1) ret = ret * tmp % p;
tmp = tmp * tmp % p;
n >>= 1;
}
return ret;
}
LL f(int p)
{
if(p == 1) return 0;
int phip = phi(p);
return qpow(2, f(phip) + phip, p);
}
void work()
{
int p;
scanf("%d", &p);
printf("%d\n", (int)f(p));
}
void Main()
{
int T;
scanf("%d", &T);
while(T--) work();
}
}
int main()
{
freopen("in.txt", "r", stdin);
MYS::Main();
return 0;
}






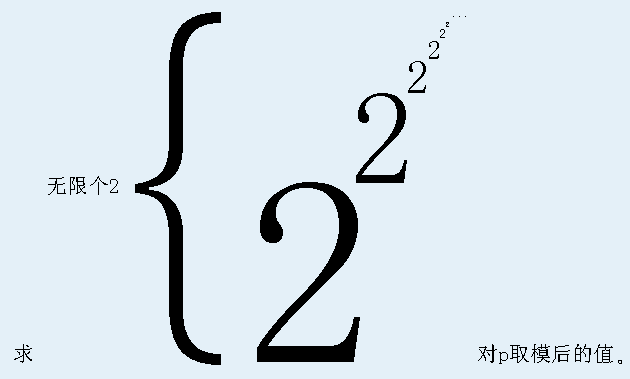
















 822
822

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








