Description
现在有一个 m * n 的整数矩阵,请你编写一个程序计算出一条从左到右穿过矩阵的路径,并使此路径的费用最小。路径从矩阵的左侧的第一列的任意单元格开始,逐步穿过矩阵到达最右侧的一列的任意单元格。每一步是指从某单元格进入它一列的相邻单元格(如下图,可以是横向或斜向)。矩阵的第一行和最后一行实际是相邻的,你可以想象矩阵是包裹在一个横放的圆柱体外面。
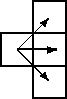
路径的花费是指这条路径所穿越的所有单元格中的数字之和。
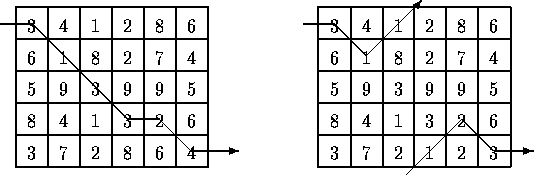
穿越两个略有不同的 5 * 6 的矩阵的路径如下图所示,这两个矩阵只有最后一行的数字不同。右侧的路径显示了第一行和最后一行相邻的效果。
Input
输入包括一系列矩阵描述。每个矩阵描述的第一行是 m 和 n,即矩阵的行数和列数;之后的 m 行,每行包括 n 个以空格分开的整数,则是当前矩阵的值,注意矩阵的值未必是正数。矩阵的行数 m 和列数 n 的范围是:1 <= m <= 10、 1 <= n <= 100;所有路径的费用值都可以用 30bit 的整数表示
Output
针对每一个矩阵,找出费用最小的路径,并将其输出。每个矩阵的输出包括两行,第一行是路径本身,即输出每一步所在的行,第二行则是该路径的费用。如果对于同一个矩阵有多条不同的费用最小路径,则输出左端行号较小的一条。
Sample Input
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 8 6 4
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 1 2 3
2 2
9 10 9 10
Sample Output
1 2 3 4 4 5
16
1 2 1 5 4 5
11
1 1
19
Solution
简单的DP,其中有几个细节,首先是输出字典序最小的可行解,这个就是倒着推,每次选择最小值中字典序最小的那个,如果只是求最小值这题就是道小水题了,重点在于怎么输出路径,因为在递推过程中可能会有很多条路径,记录比较麻烦,此处可以利用一个数组path[i][j]表示如果走到i行j列,那么下一步就要走path[i][j]行j+1列,这样一来,最终只需要确定路径起点就能通过path数组推出整条路径,而找路径起点只需要比较dp[i][1]找到最小值即可
Code
#include<stdio.h>
#include<string.h>
int dp[11][111],path[11][111];
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m))
{
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
scanf("%d",&dp[i][j]);
for(int j=m-2;j>=0;j--)
for(int i=0;i<n;i++)
{
int temp=i;
if(dp[(i+1)%n][j+1]<dp[temp][j+1]||dp[(i+1)%n][j+1]==dp[temp][j+1]&&(i+1)%n<temp)
temp=(i+1)%n;
if(dp[(i-1+n)%n][j+1]<dp[temp][j+1]||dp[(i-1+n)%n][j+1]==dp[temp][j+1]&&(i-1+n)%n<temp)
temp=(i-1+n)%n;
dp[i][j]+=dp[temp][j+1];
path[i][j]=temp;
}
int ans=1<<30,k;
for(int i=0;i<n;i++)
if(ans>dp[i][0])
{
ans=dp[i][0];
k=i;
}
printf("%d",k+1);
for(int i=0;i<m-1;i++)
{
printf(" %d",path[k][i]+1);
k=path[k][i];
}
printf("\n%d\n",ans);
}
return 0;
}























 1397
1397

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








