Description
Input
Output
Sample Input
1 2
1000 1 0
1 1000 1
Sample Output
0.001
Data Constraint
分析
这种最大化形如
∑x/∑y
的式子的题,很容易想到分数规划。
二分答案,对于当前的mid,设d[i]=p[i]-mid*s[i]
考虑到当一个节点i被选,那么fa[i]也要被选,那么一个想法是选取当前最大的d,然后把它的儿子的d放入堆里。
但是这个方法是错误的(然而我一开始就这么打了,只有10分)
题目给出的是一棵树,那么可以先dfs一遍,存下每个点的dfs序,然后设f[i][j]表示当前做到dfn为i的节点,选取了j个的最大和。设R[i]为节点i的子树中最大的dfn+1
转移有两种情况:
1. 选取i,设它原来的编号为x,那么f[i][j]+a[x]——>f[i+1][j+1]
2. 不选取i,那么f[i][j]——>f[R[i]][j] (这样就跳过了它的子树)
加上二分,时间复杂度为 O(n2logans)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef double db;
const int maxn=2505;
const db z=1e-5,Inf=-1e20;
int m,n,tot,fa[maxn],h[maxn],e[maxn],next[maxn],dfn[maxn],R[maxn];
db d[maxn],s[maxn],p[maxn],f[maxn][maxn],l,r,mid,ans;
void add(int x,int y)
{
e[++tot]=y; next[tot]=h[x]; h[x]=tot;
}
void init(int x)
{
dfn[x]=tot++;
for (int i=h[x];i;i=next[i]) init(e[i]);
R[dfn[x]]=tot;
}
int main()
{
scanf("%d%d",&m,&n);
for (int i=1;i<=n;i++)
{
scanf("%lf%lf%d",&s[i],&p[i],&fa[i]);
add(fa[i],i);
}
tot=0;
init(0);
for (l=0,r=1e4,mid=r/2;r-l>=z;mid=(l+r)/2)
{
for (int i=1;i<=n;i++)
{
d[dfn[i]]=p[i]-mid*s[i];
for (int j=0;j<=m+1;j++) f[i][j]=Inf;
}
for (int j=0;j<=m+1;j++) f[n+1][j]=Inf;
for (int i=0;i<=n;i++)
for (int j=0;j<=min(i,m+1);j++)
{
if (f[i][j]+d[i]>f[i+1][j+1]) f[i+1][j+1]=f[i][j]+d[i];
if (f[i][j]>f[R[i]][j]) f[R[i]][j]=f[i][j];
}
if (f[n+1][m+1]>=0) l=mid;else r=mid;
}
printf("%.3lf\n",mid);
return 0;
}










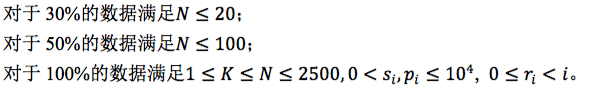














 193
193

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








