首先我们先来看什么是反素数:
反素数的定义:对于任何正整数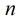
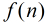
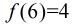
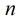
数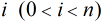
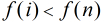
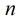
从反素数的定义中可以看出两个性质:
(1)一个反素数的所有质因子必然是从2开始的连续若干个质数,因为反素数是保证约数个数为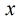
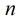
(2)同样的道理,如果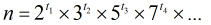
在ACM竞赛中,最常见的反素数的问题如下:
(1)求出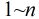
(2)给定一个数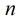
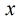
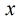
对于第一个问题来说,实质就是找出不大于n的最大的反素数。
题目链接:ZOJ1562
实现代码如下:
代码1:
#include<stdio.h>
typedef long long ll;
const int prime[16]= {1,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47};
ll maxsum, bestnum, n;
void getantiprime(ll num, ll k,ll sum,int limit)
{//num:当前枚举到的数,k:枚举到的第k大的质因子;sum:该数的约数个数;limit:质因子个数上限;
ll temp;
if(sum > maxsum)
{
maxsum = sum;
bestnum = num; //如果约数个数更多,将最优解更新为当前数;
}
if(sum==maxsum && bestnum > num)
bestnum = num; //如果约数个数相同,将最优解更新为较小的数;
if(k > 15) return;
temp = num;
for(int i=1; i<=limit; i++) //开始枚举每个质因子的个数;
{
if(temp*prime[k] > n) break;
temp = temp * prime[k]; //累乘到当前数;
getantiprime(temp, k+1, sum*(i+1), i); //继续下一步搜索;
}
}
int main()
{
while(~scanf("%lld", &n))
{
maxsum=0;
bestnum=0;
getantiprime(1,1,1,50);
printf("%lld\n", bestnum);
}
return 0;
}
代码2:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef unsigned long long ULL;
const ULL INF = ~0ULL;
int p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
ULL ans,n;
int best;
void dfs(int dept,ULL tmp,int num)
{
//到叶子结点,返回
if(dept >= 16) return;
//num记录的因子个数,如果遇到更小的,就更新
if(num > best)
{
best = num;
ans = tmp;
}
//当因子个数相同时,取值最小的
if(num == best && ans > tmp) ans = tmp;
for(int i=1;i<=63;i++)
{
if(n / p[dept] < tmp) break;
dfs(dept+1,tmp *= p[dept],num*(i+1));
}
}
int main()
{
while(cin>>n)
{
ans = INF;
best = 0;
dfs(0,1,1);
cout<<ans<<endl;
}
return 0;
}
对于第2个问题,与求因子的方法类似,先建立搜索树,然后以每一个pi为一层建立树型结构,搜索出最小的x。
题目链接:codeforce/27/E
实现代码如下:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef unsigned long long ULL;
const ULL INF = ~0ULL;
int p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
int n;
ULL ans;
void dfs(int dept,ULL tmp,int num)
{
if(num > n) return;
if(num == n && ans > tmp) ans = tmp;
for(int i=1;i<=63;i++)
{
if(ans / p[dept] < tmp) break;
dfs(dept+1,tmp *= p[dept],num*(i+1));
}
}
int main()
{
while(cin>>n)
{
ans = INF;
dfs(0,1,1);
cout<<ans<<endl;
}
return 0;
}
题目链接:http://acm.timus.ru/problem.aspx?space=1&num=1748
实现代码如下:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef unsigned long long ULL;
const ULL INF = ~0ULL;
int p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
ULL ans,n;
int best;
void dfs(int dept,int limit,ULL tmp,int num)
{
if(tmp > n) return;
if(num > best)
{
best = num;
ans = tmp;
}
if(num == best && ans > tmp) ans = tmp;
for(int i=1;i<=limit;i++)
{
double cur = (double)tmp;
if(n < cur*p[dept]) break;
dfs(dept+1,i,tmp *= p[dept],num*(i+1));
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>n;
ans = INF;
best = 0;
dfs(0,60,1,1);
cout<<ans<<" "<<best<<endl;
}
return 0;
}






















 1164
1164

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








