原题:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5235
题意:给定一个序列A,每次询问一组 L, R, 设 F(L) = AL, F(L+1) = AL+1, F(x) = F(x-1) + F(x-2) * Ax, 求F(R)
解法1:线段树
对于形如f(x) = p * f(x-1) + q * f(x-2)的通项都可以转成矩阵乘法,对于本题就是
于是依次拓展后得到
对于线段树的每个结点保存一个矩阵,如果结点是叶子,则有 a[0][0] = a[1][0] = 1, a[0][1] = Ax, a[1][1] = 0的形式
否则保存 a[r] * a[r-1] * ... * a[l] 的结果矩阵,要注意不要乘反了
于是对于每一个询问 l, r, 答案就是 find(l + 2, r) 的结果矩阵,再去乘 Al+1 Al 矩阵的结果
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <vector>
#include <map>
#include <cmath>
using namespace std;
#define LL long long
#define ULL unsigned long long
#define mod 1000000007
#define eps 1e-8
#define MP make_pair
#define mxn 100005
LL A[mxn];
int ll[mxn << 2], rr[mxn << 2];
struct Matrix {
LL a[2][2];
Matrix(){}
Matrix( int x ){
a[0][0] = a[1][0] = 1;
a[0][1] = x;
a[1][1] = 0;
}
}M[mxn << 2];
Matrix mul(Matrix A, Matrix B) {
Matrix C;
memset(C.a, 0, sizeof(C.a));
for( int i = 0; i < 2; ++i )
for( int j = 0; j < 2; ++j )
for( int k = 0; k < 2; ++k )
C.a[i][j] = (C.a[i][j] + A.a[i][k] * B.a[k][j]) % mod;
return C;
}
void build( int l, int r, int i ) {
ll[i] = l, rr[i] = r;
if( l == r ) {
M[i] = Matrix(A[l]);
return ;
}
int m = (ll[i] + rr[i]) >> 1, ls = i << 1, rs = ls | 1;
build(l, m, ls), build(m + 1, r, rs);
M[i] = mul(M[rs], M[ls]);
}
Matrix find( int l, int r, int i ) {
if( ll[i] == l && rr[i] == r ) return M[i];
int m = (ll[i] + rr[i]) >> 1, ls = i << 1, rs = ls | 1;
if( r <= m ) return find(l, r, ls);
if( l > m ) return find(l, r, rs);
return mul(find(m + 1, r, rs), find(l, m, ls));
}
int main()
{
//ios_base::sync_with_stdio(false);
int t, n, m, l, r;
cin >> t;
while( t-- ) {
cin >> n >> m;
for( int i = 1; i <= n; ++i ) scanf( "%lld", A + i );
build(1, n, 1);
while( m-- ) {
scanf( "%d%d", &l, &r );
if( r - l <= 1 ) printf( "%lld\n", A[r] );
else {
Matrix C = find(l + 2, r, 1);
LL ans = C.a[0][0] * A[l+1] % mod + C.a[0][1] * A[l] % mod;
printf( "%lld\n", ans % mod );
}
}
}
return 0;
}解法2:分块
比赛的时候智商结石了,可耻的分块了:D
假设序列从F1开始,由于F(x) = F(x-1) + F(x-2) * Ax ,可知 F1 和 F2 永远不会乘在同一个多项式内
故设 F(x) = B(x) + C(x), 其中B(x)为含有F1的多项式之和,C(x)为含有F2的多项式之和
于是我们把序列分成长为300的段,每段令F1 = F2 = 1,序列的第1个数做为F3,依次推到后面
那么对于一组确定的F1, F2, 我们有 F(x) = B(x) * F1 + C(x) * F2
当询问区间长度小于300时,可以直接撸,大于300时,先找到第一个大于l + 1的段,然后从Fl推到这个段的前面
由于我们把每段的头做为F3, 所以上一段的最后两个数,就是这一段的 F1, F2,代入即可
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <vector>
#include <map>
#include <cmath>
using namespace std;
#define LL long long
#define ULL unsigned long long
#define mod 1000000007
#define eps 1e-8
#define MP make_pair
#define mxn 110005
LL A[mxn], B[mxn], C[mxn], F[mxn];
void init( int n ) {
for( int i = 1; i <= n; i += 300 ) {
B[i] = A[i]; C[i] = 1;
B[i+1] = A[i]; C[i+1] = A[i+1] + 1;
for( int j = i + 2; j < i + 300; ++j ) {
B[j] = (B[j-1] + B[j-2] * A[j]) % mod;
C[j] = (C[j-1] + C[j-2] * A[j]) % mod;
}
}
}
int main()
{
//ios_base::sync_with_stdio(false);
int t, n, m, l, r;
cin >> t;
while( t-- ) {
cin >> n >> m;
for( int i = 1; i <= n; ++i ) scanf( "%lld", A + i );
init(n);
while( m-- ) {
scanf( "%d%d", &l, &r );
if( r - l <= 350 ) {
F[l] = A[l];
F[l+1] = A[l+1];
for( int i = l + 2; i <= r; ++i )
F[i] = (F[i-1] + F[i-2] * A[i]) % mod;
printf( "%lld\n", F[r] );
continue;
}
int k = 1;
while( k <= l + 1 ) k += 300;
F[l] = A[l]; F[l+1] = A[l+1];
for( int i = l + 2; i < k; ++i )
F[i] = (F[i-1] + F[i-2] * A[i]) % mod;
for( int i = k, j; ; i = j ) {
j = i + 300;
if( j <= r ) {
F[j-2] = (B[j-2] * F[i-2] % mod + C[j-2] * F[i-1] % mod) % mod;
F[j-1] = (B[j-1] * F[i-2] % mod + C[j-1] * F[i-1] % mod) % mod;
}
else {
F[r] = (B[r] * F[i-2] % mod + C[r] * F[i-1] % mod) % mod;
printf( "%lld\n", F[r] );
break;
}
}
}
}
return 0;
}




 本文介绍了解决动态序列问题的两种算法:线段树和分块法。线段树通过矩阵乘法优化通项公式,适用于快速计算任意区间序列值。分块法则通过预先计算序列前缀和,实现区间查询的快速响应,特别适用于区间长度较长的情况。通过实例分析和代码实现,详细阐述了两种方法的原理和应用。
本文介绍了解决动态序列问题的两种算法:线段树和分块法。线段树通过矩阵乘法优化通项公式,适用于快速计算任意区间序列值。分块法则通过预先计算序列前缀和,实现区间查询的快速响应,特别适用于区间长度较长的情况。通过实例分析和代码实现,详细阐述了两种方法的原理和应用。
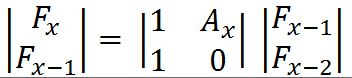
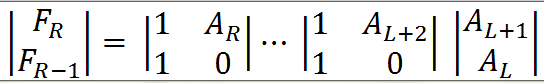
















 336
336

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








