设第n个五边形数为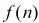
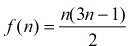
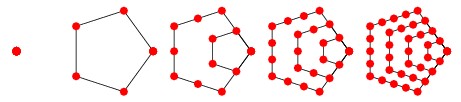
对应图形如下:
设五边形数的生成函数为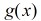
以上是五边形数的情况。下面是关于五边形数定理的内容:
五边形数定理是一个由欧拉发现的数学定理,描述欧拉函数展开式的特性。欧拉函数的展开式如下:
欧拉函数展开后,有些次方项被消去,只留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为广义五边形数。
五边形数和分割函数的关系
欧拉函数的倒数是分割函数的母函数,亦即:
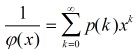
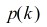
上式配合五边形数定理,有:
在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
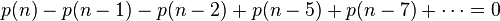
因此可得到分割函数p(n)的递归式:
例如n=10时,有: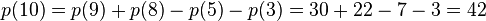
所以,通过上面递归式,我们可以很快速地计算n的整数划分方案数p(n)了。
题目: http://acm.hdu.edu.cn/showproblem.php?pid=4651
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N=100005;
const LL MOD=1000000007;
LL ans[N],tmp[N];
void Init()
{
int t=1000;
for(int i=-1000;i<=1000;i++)
tmp[i+t]=i*(3*i-1)/2;
ans[0]=1;
for(int i=1;i<N;i++)
{
ans[i]=0;
for(int j=1;j<=i;j++)
{
if(tmp[j+t]<=i)
{
if(j&1) ans[i]+=ans[i-tmp[j+t]];
else ans[i]-=ans[i-tmp[j+t]];
}
else break;
ans[i]=(ans[i]%MOD+MOD)%MOD;
if(tmp[t-j]<=i)
{
if(j&1) ans[i]+=ans[i-tmp[t-j]];
else ans[i]-=ans[i-tmp[t-j]];
}
else break;
}
ans[i]=(ans[i]%MOD+MOD)%MOD;
}
}
int main()
{
int t,n;
Init();
cin>>t;
while(t--)
{
cin>>n;
cout<<ans[n]<<endl;
}
return 0;
}
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4658
题意:问一个数n能被拆分成多少种方法,且每一种方法里数字重复个数不能超过k(等于k)。
分析递推式为:
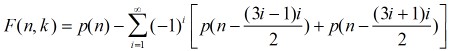
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
const int N = 100005;
const int MOD = 1000000007;
int dp[N];
void Init()
{
dp[0] = 1;
for(int i=1;i<N;i++)
{
dp[i] = 0;
for(int j=1;;j++)
{
int t = (3*j-1)*j / 2;
if(t > i) break;
int tt = dp[i-t];
if(t+j <= i) tt = (tt + dp[i-t-j])%MOD;
if(j&1) dp[i] = (dp[i] + tt)%MOD;
else dp[i] = (dp[i] - tt + MOD)%MOD;
}
}
}
int Work(int n,int k)
{
int ans = dp[n];
for(int i=1;;i++)
{
int t = k*i*(3*i-1) / 2;
if(t > n) break;
int tt = dp[n-t];
if(t + i*k <= n) tt = (tt + dp[n-t-i*k])%MOD;
if(i&1) ans = (ans - tt + MOD)%MOD;
else ans = (ans + tt)%MOD;
}
return ans;
}
int main()
{
Init();
int n,k,t;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
printf("%d\n",Work(n,k));
}
return 0;
}





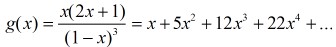
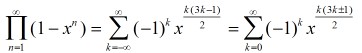
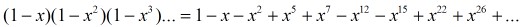
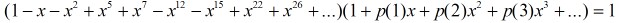
















 2901
2901










