只做梳理,不做证明 (因为不会证)
五边形数
图片摘自百度百科。
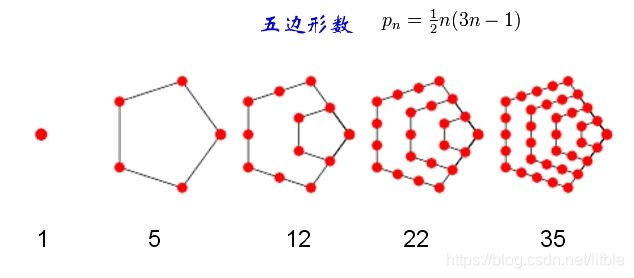
可以发现, g i = g i − 1 + 3 ( i − 1 ) + 1 g_i=g_{i-1}+3(i-1)+1 gi=gi−1+3(i−1)+1,所以通向就是 g i = i ( 3 i − 1 ) 2 g_i=\frac{i(3i-1)}{2} gi=2i(3i−1)
而广义的五边形数, i i i的取值为 0 , 1 , − 1 , 2 , − 2 , 3 , − 3... 0,1,-1,2,-2,3,-3... 0,1,−1,2,−2,3,−3...,广义五边形数的前几项为: 0 , 1 , 2 , 5 , 7 , 12 , 15 , 22 , 26... 0,1,2,5,7,12,15,22,26... 0,1,2,5,7,12,15,22,26...
欧拉函数
著名的欧拉函数 ϕ ( x ) \phi(x) ϕ(x),表示比 x x x小的与 x x x互质的数字个数,写出它的生成函数,经过一些奥妙重重的推理,有:
ϕ ( x ) = ∏ i = 1 n ( 1 − x i ) \phi(x)=\prod_{i=1}^n (1-x^i) ϕ(x)=i=1∏n(1−xi)
然后经过一些奥妙重重的推理,有:
ϕ ( x ) = ∑ − i n f i n f ( − 1 ) i x i ( 3 i − 1 ) 2 \phi(x)=\sum_{-inf}^{inf} (-1)^i x^{\frac{i(3i-1)}{2}} ϕ(x)=−inf∑inf(−1)ix2i(3i−1)
即
ϕ ( x ) = 1 − x − x 2 + x 5 + x 7 − x 12 − x 15 + . . . \phi(x)=1-x-x^2+x^5+x^7-x^{12}-x^{15}+... ϕ(x)=1−x−x2+x5+x7−x12−x15+...
拆分数
拆分数 P ( x ) P(x) P(x),就是把 x x x拆分成若干个正整数的方案数。例如对于 3 3 3,有拆分 3 = 1 + 1 + 1 3=1+1+1 3=1+1+1, 3 = 1 + 2 3=1+2 3=1+2, 3 = 3 3=3 3=3三种,所以 P 3 = 3 P_3=3 P3=3
利用1取多少个,2取多少个,3取多少个,这样的思想,得到:
P ( x ) = ∏ i = 1 i n f ( ∑ j = 0 i n f x i j ) = ∏ i = 1 i n f 1 1 − x i P(x)=\prod_{i=1}^{inf}(\sum_{j=0}^{inf} x^{ij})=\prod_{i=1}^{inf}\frac{1}{1-x^i} P(x)=i=1∏inf(j=0∑infxij)=i=1∏inf1−xi1
即 P ( x ) ϕ ( x ) = 1 P(x)\phi(x)=1 P(x)ϕ(x)=1
暴力展开,除了0次项以外,每一项的系数都要为 0 0 0,所以对于任意一个 n n n,有:
P n − P n − 1 − P n − 2 + P n − 5 + P n − 7 − P n − 12 − P n − 15 + . . . = 0 P_n-P_{n-1}-P_{n-2}+P_{n-5}+P_{n-7}-P_{n-12}-P_{n-15}+...=0 Pn−Pn−1−Pn−2+Pn−5+Pn−7−Pn−12−Pn−15+...=0
由于五边形数的大小是平方级别的,所以我们可以在 O ( n n ) O(n \sqrt{n}) O(nn)的时间内算出 1 1 1到 n n n的五拆分数。
代码
HDU4651
#include<bits/stdc++.h>
using namespace std;
#define RI register int
const int mod=1000000007,N=100000;
int qm(int x) {return x>=mod?x-mod:x;}
int js,n,T,f[N+5],g[N+5];
int main()
{
for(RI i=1;;++i) {
if(i*(3*i-1)/2<=N) g[++js]=i*(3*i-1)/2;
else break;
if(i*(3*i+1)/2<=N) g[++js]=i*(3*i+1)/2;
else break;
}
f[0]=1;
for(RI i=1;i<=N;++i) {
for(RI j=1;j<=js&&g[j]<=i;++j)
if(((j+1)/2)&1) f[i]=qm(f[i]+f[i-g[j]]);
else f[i]=qm(f[i]-f[i-g[j]]+mod);
}
scanf("%d",&T);
while(T--) scanf("%d",&n),printf("%d\n",f[n]);
return 0;
}
有限制的拆分数
要求拆分后,每一种数字不能用大于等于 k k k次。
那么写出生成函数:
∏ i = 1 i n f ( 1 + x i + x 2 i + . . . + x ( k − 1 ) i ) = ∏ i = 1 i n f 1 − x k i 1 − x i = ϕ ( x k ) ϕ ( x ) \prod_{i=1}^{inf} (1+x^i+x^{2i}+...+x^{(k-1)i})=\prod_{i=1}^{inf} \frac{1-x^{ki}}{1-x^i}=\frac{\phi(x^k)}{\phi(x)} i=1∏inf(1+xi+x2i+...+x(k−1)i)=i=1∏inf1−xi1−xki=ϕ(x)ϕ(xk)
所以这个生成函数 F ( x ) F(x) F(x)满足( P ( x ) P(x) P(x)还是指拆分数的生成函数): F ( x ) = P ( x ) ϕ ( x k ) F(x)=P(x)\phi(x^k) F(x)=P(x)ϕ(xk)
同样,暴力展开卷积,则有: f x = P x − P x − k − P x − 2 k + P x − 5 k + P x − 7 k − P x − 12 k − P x − 15 k + . . . f_x=P_x-P_{x-k}-P_{x-2k}+P_{x-5k}+P_{x-7k}-P_{x-12k}-P_{x-15k}+... fx=Px−Px−k−Px−2k+Px−5k+Px−7k−Px−12k−Px−15k+...
还是可以 O ( n n ) O(n \sqrt{n}) O(nn)地做。
另外有一个奥妙重重的结论,就是拆分成的数都是奇数的方案数,等于拆分成完全不同的数(也就是每一种数使用不超过1次)的方案数。
代码
HDU4658
#include<bits/stdc++.h>
using namespace std;
#define RI register int
const int mod=1000000007,N=100000;
int qm(int x) {return x>=mod?x-mod:x;}
int js,n,K,T,f[N+5],g[N+5];
int main()
{
for(RI i=1;;++i) {
if(i*(3*i-1)/2<=N) g[++js]=i*(3*i-1)/2;
else break;
if(i*(3*i+1)/2<=N) g[++js]=i*(3*i+1)/2;
else break;
}
f[0]=1;
for(RI i=1;i<=N;++i) {
for(RI j=1;j<=js&&g[j]<=i;++j)
if(((j+1)/2)&1) f[i]=qm(f[i]+f[i-g[j]]);
else f[i]=qm(f[i]-f[i-g[j]]+mod);
}
scanf("%d",&T);
while(T--) {
scanf("%d%d",&n,&K);
int ans=f[n];
for(RI i=1;i<=js&&g[i]*K<=n;++i)
if(((i+1)/2)&1) ans=qm(ans-f[n-g[i]*K]+mod);
else ans=qm(ans+f[n-g[i]*K]);
printf("%d\n",ans);
}
return 0;
}
























 643
643

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








