尊重原创转载请注明:From AigeStudio(http://blog.csdn.net/aigestudio)Power by Aige 侵权必究!
炮兵
PS:写得太嗨忘了说明一点,下面文章中提到的“长边”(也就是代码部分中出现的sizeLong)指的是折叠区域直角三角形中与控件右边相连的边,而“短边”(也就是代码部分中出现的sizeShort)则指的是折叠区域直角三角形中与控件底边相连的边。两者术语并非指的是较长的边和较短的边,这点要注意。其命名来源于My参考图…………囧……
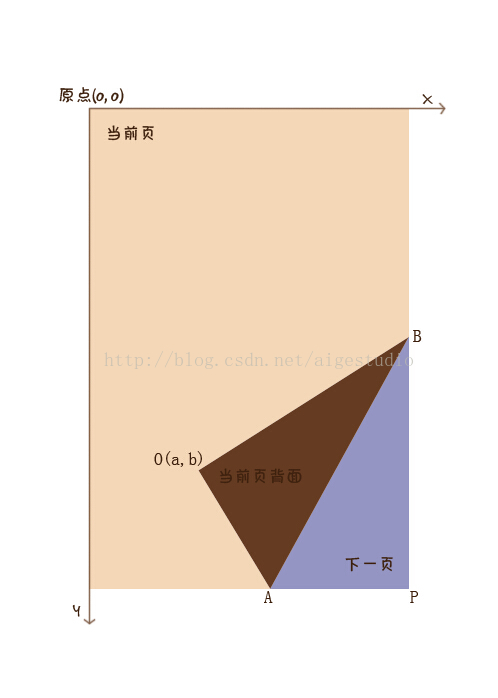
上一节中我们讲了翻页的原理实现,说白了就是Canvas中clip方法的使用,而现实生活中的翻页必然不是像我们上节demo那样左右切换的,我们总是会在看书翻页的时候掀起纸张的一角拉向书的另一侧实现翻页,翻页的过程对纸张来说是一个曲度和形状改变的过程,这一节我们先不讲曲度的实现,我们先假设翻页的过程是一个折页的过程,类似下图:
先以折页的方式对翻页过程进行一个细致的分析,然后再在下一节将折线变为曲线。折页的实现可分为两种方式,一种是纯计算,我们利用已知的条件根据各类公式定理计算出未知的值,第二种呢则是通过图形的组合巧妙地去获取图形的交并集来实现,第二种方式需要很好的空间想象力这里就先不说了,而第一种纯计算的方式呢又可以分为使用高等数学和解三角形两种方法,前者对于数学不好的童鞋来说不易理解,这里我们选择后者使用解三角形来计算,首先我们先来搞个简单的辅助图:
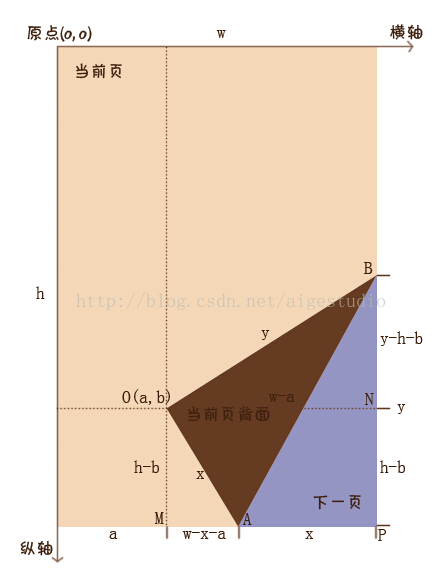
图很简单,一看就懂,大家可以拿个本子或者书尝试折页,不管你如何折,折叠区域AOB和下一页显示的区域APB必定是完全相等的对吧,那么我们就可以得到一个惊人的事实:角AOB恒为直角,这时我们来添加一些辅助线便于理解:
我们设折叠后的三角形AOB的短边长度为x而长边长度为y,由图可以得出以下运算:
我们可以使用相同的方法去解得y的值,这里我使用的是等面积法,由图可知梯形MOBP的面积是三角形MOA、AOB、APB面积之和:
这样我们可以根据任意一点得出两边边长,我们来代码中实践一下看看是不是这样的呢?为了便于理解,这里我重新使用了一个新的FoldView:
public class FoldView extends View {
public FoldView(Context context, AttributeSet attrs) {
super(context, attrs);
}
}@Override
protected void onDraw(Canvas canvas) {
// 重绘时重置路径
mPath.reset();
// 绘制底色
canvas.drawColor(Color.WHITE);
/*
* 如果坐标点在右下角则不执行绘制
*/
if (pointX == 0 && pointY == 0) {
return;
}
/*
* 额,这个该怎么注释好呢……根据图来
*/
float mK = mViewWidth - pointX;
float mL = mViewHeight - pointY;
// 需要重复使用的参数存值避免重复计算
float temp = (float) (Math.pow(mL, 2) + Math.pow(mK, 2));
/*
* 计算短边长边长度
*/
float sizeShort = temp / (2F * mK);
float sizeLong = temp / (2F * mL);
/*
* 生成路径
*/
mPath.moveTo(pointX, pointY);
mPath.lineTo(mViewWidth, mViewHeight - sizeLong);
mPath.lineTo(mViewWidth - sizeShort, mViewHeight);
mPath.close();
// 绘制路径
canvas.drawPath(mPath, mPaint);
}
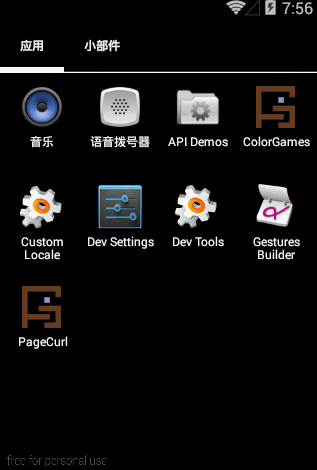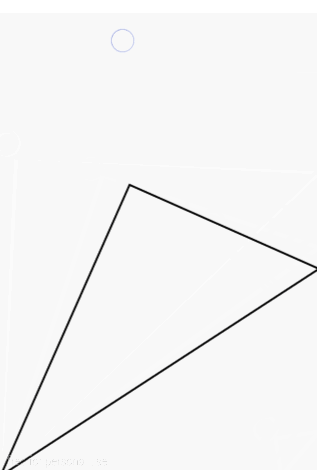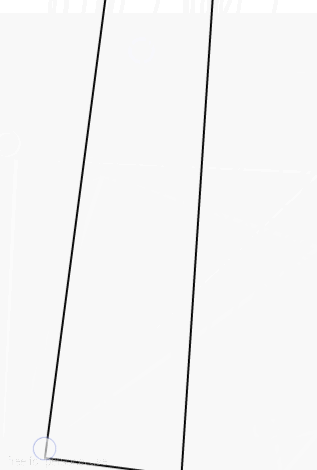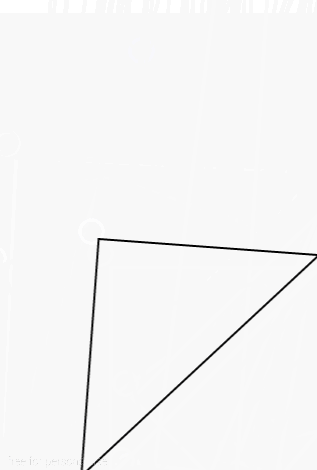
效果是大致出来了,但是我们发现有一处不对的地方,当我们非常靠左或非常靠下地折叠时:
如果再往下折
如果再往左折
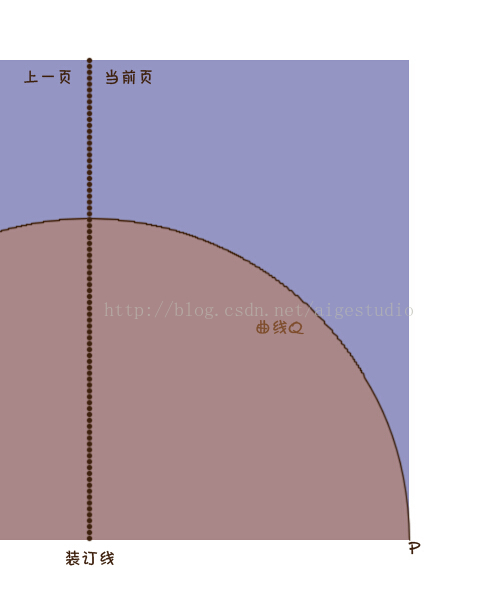
此时我们的Path就会消失掉,其实这跟我们我们现实中的折页是一样的,折页的过程是有限制的,如下图:
右下角点P因为受装订线的制约,其半径最大只能为纸张的宽度,如果我们始终以该宽度为半径折页,那么点P的轨迹就可以形成曲线Q,图中半透明红色区域为一个半圆形,也就是说,我们的点P只能在该范围内才应当有效对吧,那么该如何做限制呢?很简单,我们只需在计算长短边长之前判断触摸点是否在该区域即可:
/**
* 计算短边的有效区域
*/
private void computeShortSizeRegion() {
// 短边圆形路径对象
Path pathShortSize = new Path();
// 用来装载Path边界值的RectF对象
RectF rectShortSize = new RectF();
// 添加圆形到Path
pathShortSize.addCircle(0, mViewHeight, mViewWidth, Path.Direction.CCW);
// 计算边界
pathShortSize.computeBounds(rectShortSize, true);
// 将Path转化为Region
mRegionShortSize.setPath(pathShortSize, new Region((int) rectShortSize.left, (int) rectShortSize.top, (int) rectShortSize.right, (int) rectShortSize.bottom));
}/*
* 判断触摸点是否在短边的有效区域内
*/
if (!mRegionShortSize.contains((int) mPointX, (int) mPointY)) {
// 如果不在则通过x坐标强行重算y坐标
mPointY = (float) (Math.sqrt((Math.pow(mViewWidth, 2) - Math.pow(mPointX, 2))) - mViewHeight);
// 精度附加值避免精度损失
mPointY = Math.abs(mPointY) + mValueAdded;
}/*
* 缓冲区域判断
*/
float area = mViewHeight - mBuffArea;
if (mPointY >= area) {
mPointY = area;
}
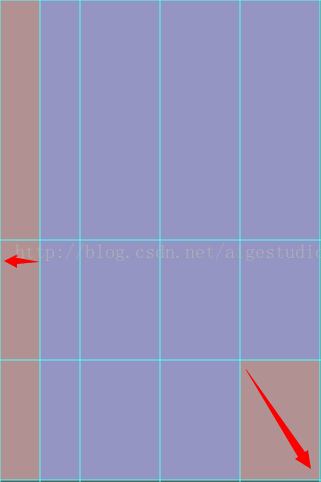
大致的效果出来了,我们还需要做一些补充工作,当触摸点在右下角某个区域时如果我们抬起手指,那么就让“纸张”自动滑下去,同理当触摸点在左边某个区域时我们让“纸张”自动翻过去,这里我们约定这两个区域分别是控件右下角宽高四分之一的区域和控件左侧八分之一的区域(当然你可以约定你自己的控件行为,这里我就哪简单往哪走了~):
那么在上一节中我们也有类似的效果,这里我们依葫芦画瓢,当手指抬起时判断当前事件点是否位于右下角自滑区域内,如果在那么以当前事件点为坐标点A右下角为坐标点B根据两点式我们可以获得一条直线方程:
此后根据不断自加递增的x坐标不断计算对应的y坐标直至点滑至右下角为止,既然涉及到事件,So我们在onTouchEvent处理:
case MotionEvent.ACTION_UP:// 手指抬起时候
/*
* 获取当前事件点
*/
float x = event.getX();
float y = event.getY();
/*
* 如果当前事件点位于右下自滑区域
*/
if (x > mAutoAreaRight && y > mAutoAreaButtom) {
// 获取当前点为直线方程坐标之一
float startX = x, startY = y;
/*
* 当x坐标小于控件宽度时
*/
while (x < mViewWidth) {
// 不断让x自加
x++;
// 重置当前点的值
mPointX = x;





 本文介绍了Android中实现翻页效果的一种折线方法,通过解三角形计算折页过程中的边长,确保翻页区域与下一页显示区域相等。在折线的基础上,文章还讨论了如何限制触摸点的范围,防止Path消失,并在手指抬起时实现自动滑动效果。此外,通过Handler更新View来实现滑动动画,解决了invalidate()在循环中无法立即刷新的问题。最后,处理了Path过大导致的渲染警告,通过调整计算方式避免不必要的绘制。
本文介绍了Android中实现翻页效果的一种折线方法,通过解三角形计算折页过程中的边长,确保翻页区域与下一页显示区域相等。在折线的基础上,文章还讨论了如何限制触摸点的范围,防止Path消失,并在手指抬起时实现自动滑动效果。此外,通过Handler更新View来实现滑动动画,解决了invalidate()在循环中无法立即刷新的问题。最后,处理了Path过大导致的渲染警告,通过调整计算方式避免不必要的绘制。

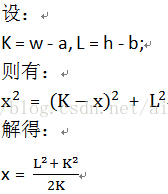



 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1200
1200

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








