【日常学习】【数学/哈希】康托展开

康托展开是什么呢？

（以下内容引自CSDN用户zhongkeli 原文地址：http://blog.csdn.net/zhongkeli/article/details/6966805

其实这位作者也是引用的博客园用户的文章，但是原文已经找不到了，因此放上转载作者作为来源，尊重原作者版权。）

康托展开的公式是 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! 其中，ai为当前未出现的元素中是排在第几个（从0开始）。
　　这个公式可能看着让人头大，最好举个例子来说明一下。例如，有一个数组 s = ["A", "B", "C", "D"]，它的一个排列 s1 = ["D", "B", "A", "C"]，现在要把 s1 映射成 X。n 指的是数组的长度，也就是4，所以
X(s1) = a4*3! + a3*2! + a2*1! + a1*0!

关键问题是 a4、a3、a2 和 a1 等于啥？

a4 = "D" 这个元素在子数组 ["D", "B", "A", "C"] 中是第几大的元素。"A"是第0大的元素，"B"是第1大的元素，"C" 是第2大的元素，"D"是第3大的元素，所以 a4 = 3。
a3 = "B" 这个元素在子数组 ["B", "A", "C"] 中是第几大的元素。"A"是第0大的元素，"B"是第1大的元素，"C" 是第2大的元素，所以 a3 = 1。
a2 = "A" 这个元素在子数组 ["A", "C"] 中是第几大的元素。"A"是第0大的元素，"C"是第1大的元素，所以 a2 = 0。
a1 = "C" 这个元素在子数组 ["C"] 中是第几大的元素。"C" 是第0大的元素，所以 a1 = 0。（因为子数组只有1个元素，所以a1总是为0）
所以，X(s1) = 3*3! + 1*2! + 0*1! + 0*0! = 20

对于每一种排列，康托展开后，编号分别为：
A B C | 0
A C B | 1
B A C | 2
B C A | 3
C A B | 4
C B A | 5

说到这里，大家差不多久都明白了吧。康托展开，是用一一对应的方式将一些元素的排列映射为一组从1开始的连续数字。因此，如果在哈希表中用到它，不必取模，计算过程也没有复杂多少，但大大减少了哈希数组的空间复杂度，使得哈希数组空间利用率达到100%。哈希数组大小是n！（n为元素个数）。

那么，我们引用CSDN用户Re_cover的康托展开的代码（源地址：http://blog.csdn.net/re_cover/article/details/9823169）：

int factor[] = {1,1,2,6,24,120,720,5040,40320,362880};//阶乘   

int cantor(char x[]) //康托展开   
{  
    int sum = 0, s;  
    for(int i = 0; i < 9; i++)  
    {  
        s = 0;  
        for(int j = i + 1; j < 9; j++)  
            if(x[j] < x[i])  
                s++;  
        sum += s * factor[9 - i - 1];  
    }  
    return sum;  
}  

通过康托逆展开生成全排列


如果已知 s = ["A", "B", "C", "D"]，X(s1) = 20，能否推出 s1 = ["D", "B", "A", "C"] 呢？
因为已知 X(s1) = a4*3! + a3*2! + a2*1! + a1*0! = 20，所以问题变成由 20 能否唯一地映射出一组 a4、a3、a2、a1？如果不考虑 ai 的取值范围，有
3*3! + 1*2! + 0*1! + 0*0! = 20
2*3! + 4*2! + 0*1! + 0*0! = 20
1*3! + 7*2! + 0*1! + 0*0! = 20
0*3! + 10*2! + 0*1! + 0*0! = 20
0*3! + 0*2! + 20*1! + 0*0! = 20
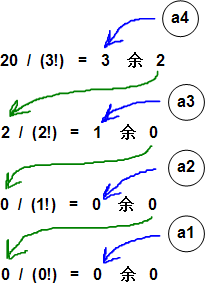
等等。但是满足 0 <= ai <= n-1 的只有第一组。可以使用辗转相除的方法得到 ai，如下图所示：

知道了a4、a3、a2、a1的值，就可以知道s1[0] 是子数组["A", "B", "C", "D"]中第3大的元素 "D"，s1[1] 是子数组 ["A", "B", "C"] 中第1大的元素"B"，s1[2] 是子数组 ["A", "C"] 中第0大的元素"A"，s[3] 是子数组 ["C"] 中第0大的元素"C"，所以s1 = ["D", "B", "A", "C"]。
这样我们就能写出一个函数，它可以返回  s 的第 m 个排列。

这里同样引用Re_cover的代码：

void trans(int x) //康托展开逆运算   
{  
    int visit[10] = {0};  
    int t;  
    for(int i = 0; i < 9; i++)  
    {  
        t = x / factor[9 - i - 1];  
        x %= factor[9 - i - 1];  
        for(int j = 0; j <= t; j++)  
            if(visit[j] == 1)  
                t++;  
        visit[t] = 1;  
        st[i] = t;  
    }  
}  

至此，康托展开的学习就告一段落了。最后想介绍一下康托，虽然估计大家也都认识他吧，格奥尔格·康托，集合论的发明者，一生执着追求的异类。我们的数学老师只发过一篇补充阅读材料，介绍的就是康托。他是幸运的，他求学时，正值柏林大学形成欧洲数学中心的时代，他的导师是大数学家库莫尔，外尔斯特拉斯和克罗内克。他又是不幸的，他的集合论如罗巴切夫斯基的鞍面几何那样不为世人所接受，但罗巴切夫斯基至少还有在内心里默默支持他的高斯，而康托的学说即使他的恩师克罗内克都是最激进的反对者。孤独而执着地坚持着自己的学说的康托最终罹患严重的精神分裂，在痛苦和绝望中死去。直到他死后很多年，人们才重新发现集合论的重要性。如今集合论已成为中学数学最为基础的第一课。让我们缅怀这位抗争一生的数学家。

顺带也缅怀一下同样孤独一生的罗巴切夫斯基，他曾巡回欧洲演讲，然而无人能回应他殷切的期待。正如高斯日记里所说：“当时在场的各位，我或许是其中唯一听懂罗巴切夫斯基先生在说什么的人。”然而高斯的软弱和怯懦让他没有勇气公开支持这一在他内心已然成熟却被视为异端的理论，这让罗氏进一步陷入冰窖，仿佛这一成果成了他一生的污点。最让我感动的是，尽管孤独落寞，他至死都坚信这一成果的正确性，坚信这是一种独立于欧式几何的几何系统。

相比之下，黎曼的境遇就要好上很多。在人们的思想进一步解放后，年轻的波恩哈德·黎曼（时年28岁）拿着一篇赫然写着平行线可以相交的论文来到歌厅根大学，当即被聘为讲师。（北师大的老教授在这里吐槽说由此可见当时德国大学数学是什么样的水平= =好喜欢萌哒哒老爷爷）这篇论文奠定了黎曼几何的基础。黎曼几何是球面几何，与罗氏几何的鞍面不同，但产生的影响愈发广大。它深刻地影响了拓扑学，在爱因斯坦以它为基础发明广义相对论后更是被世人奉若珍宝。而罗巴切夫斯基也终于得以正名。

好了，科学史就说到这里吧。仰望满天的星空，缅怀逝去的先辈，让我们努力为人类科学进步做出更大的努力。

——千里之行，始于足下。