Brent原理（Brent’s Principle）

在将一个问题的内在并行性(inherent parallelism)转化为一个有效的并行算法时，Brent原理（Brent’s Principle）为这种并行化提供了一个普遍的模式。该结论最初由Richard P. Brent于1974年给出（可以参见文献【3】）。

Brent’s Principle：考虑一个计算（或算法）C，在提供足够多的处理器资源之前提下（并忽略操作之间用于交互的耗时），算法C能够在PRAM上以时间 t 完成（也就是需要t个并行的步骤），假设mi表示第 i 个步骤涉及到的操作数量，并且令

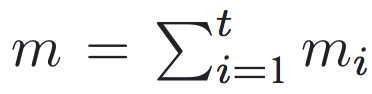
那么当给定 p 个处理器时，并且要求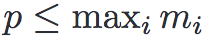，（相同计算量的）算法C可以在时间Tp内（即Tp个步骤内）完成，而且Tp小于等于 t+(mi-t)/p 时间完成。

证明：直觉上，如果第 i 个步骤需要执行mi个操作，当有 p 个处理器时，那么它可以在如下时间内被模拟

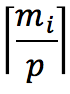
而且上式必然满足：

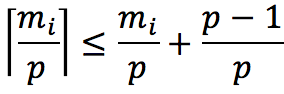
既然共有t个并行的步骤，所以把它们加和，可得

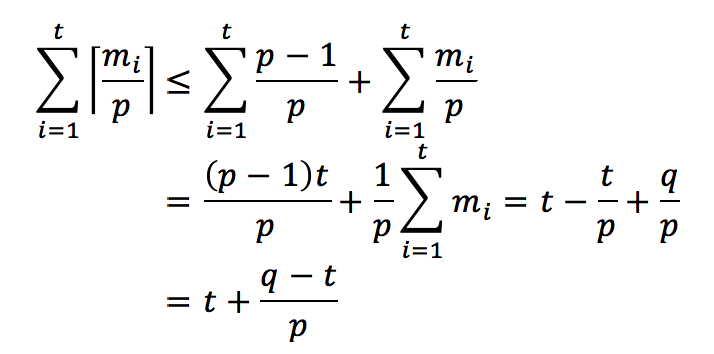
结论得证。
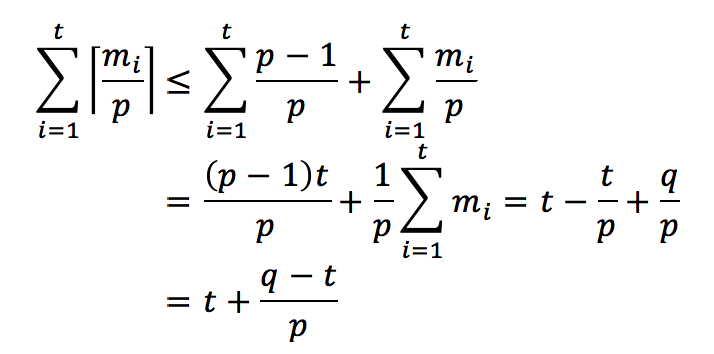
注意文献【2】中所给的形式略有不同，因为在第一个不等式处，它所采用的上限稍有修改。但是二者之结论都是统一的。



参考文献及推荐阅读材料：
【1】Dr Aaron Harwood，The University of Melbourne 并行与多核计算课程材料
【2】John E. Savage，Models of Computation：Exploring the Power of Computing，Chapter 7, Brown University

【3】R. P. Brent, “The Parallel Evaluation of General Arithmetic Expressions,” JACM 21 (1974), pp:201–206.