归并排序
采用分治(Divide and Conquer)思想。
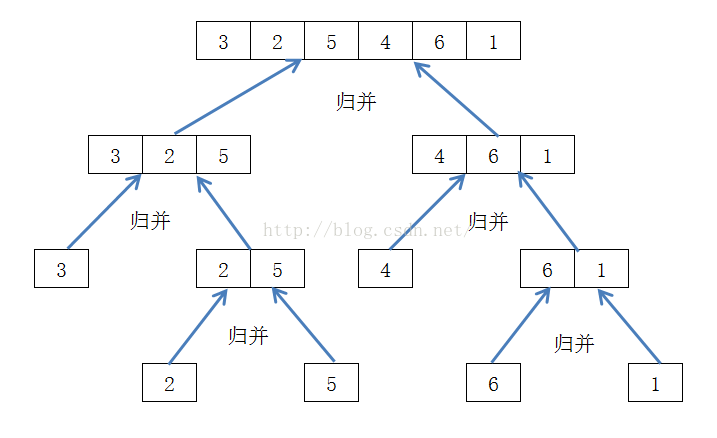
主要思想:将数组分成两部分,如果这两部分均有序,那么便可在O(n)的时间内合并成一个完整的有序数组。
采用分治(Divide and Conquer)思想。
主要思想:将数组分成两部分,如果这两部分均有序,那么便可在O(n)的时间内合并成一个完整的有序数组。
以此类推将区间划分下去,直到每个区间只有一个元素,即可认为已经有序,然后两两合并。
求解递归式可得归并排序的时间复杂度为T(n)=O(nlgn)
归并排序是一种稳定的排序算法
归并排序主要在于合并过程,合并两个有序数组的过程如下
public int[] merge(int[] a, int[] b) {
int[] result = new int[a.length + b.length];
int i = 0, j = 0, k = 0;
while (i < a.length && j < b.length) {
if (a[i] <= b[j]) {
result[k++] = a[i++];
} else {
result[k++] = b[j++];
}
}
while (i < a.length) {
result[k++] = a[i++];
}
while (j < b.length) {
result[k++] = b[j++];
}
return result;
}public void sortMerger(int[] a, int p, int q) {
if (p < q) {
int r = (q + p) / 2;
sortMerger(a, p, r);
sortMerger(a, r + 1, q);
merge(a, p, r, q);
}
}private void merge(int[] a, int p, int r, int q) {
int size = q - p + 1;
int arr[] = new int[size];
int i = p, k = 0;
int j = r + 1;
while (i <= r && j <= q) {
if (a[i] <= a[j]) {
arr[k++] = a[i++];
} else {
arr[k++] = a[j++];
}
}
while (i <= r)
arr[k++] = a[i++];
while (j <= q)
arr[k++] = a[j++];
// 数组arr[]里面已经保存了排好序的元素
for (int x = 0; x < q - p + 1; x++) { // q-p+1 == size
a[p + x] = arr[x];
}
}
























 577
577

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








