贪婪算法

0） 引论

贪婪算法是分阶段进行的一种算法，每一个阶段，我们只取最好的决策，而不管以后。贪婪算法是“take what you can get now”策略。

贪婪算法的结果一般会取到的是局部最优值而非全局最优的，一般情况下这两个值是不相等的，但是很多情况下，可以用局部最优值来模拟近似全局最优值。

常用的图论中的Dijkstra算法以及Kruskal算法都利用了贪婪算法的思想。

贪婪算法的一个典型例子是零钱兑换：

假设需要兑换16快钱的零钱，同时假设货币有10元，5元，1元的，同时我们定义钱的个数第为优，那么利用贪婪算法的兑换结果为一个10元，一个5元，一个1元，这个是全局最优解。但是假设货币有12元，10元，5元，1元的，那么利用贪婪算法的兑换结果为一个12元，四个1元，这个就不是最优解了，最优解仍是一个10元，一个5元，一个1元。

因此我们可以看到贪婪算法是无法保证最优解的，它只是提供了一个分段解决问题的思想，得到的结果只是局部最优。

1） 简单的调度问题

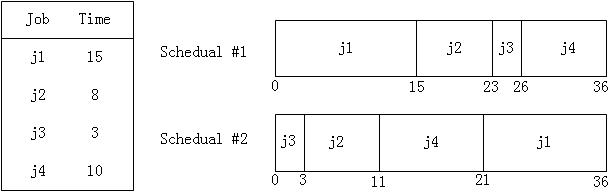
假设一个单核CPU有下面的4个任务，现在求这四个任务的平均完成时间。

一种方法是上面的Schedual #1,也就是按照Job的先后顺序来工作，那么平均完成时间为（15+（15+8）+（15+8+3）+（15+8+3+10））/4 = 25.

而一种方法是上面的Schedual #2,也就是先处理时间小的Job，那么平均完成时间为（3+（3+8）+（3+8+10）+（3+8+10+15））/4 = 17.75.

Schedual #2就是一种贪婪算法，每一个阶段只处理最好的值，在这里就是运行时间最短。这里贪婪算法能够取得最好的结果

2） 多线程调度问题

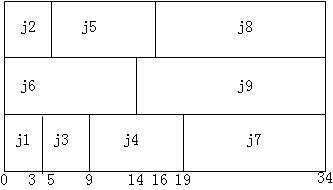
假设我们有多个CPU，同时进行以下的任务，要求这些任务的平均完成时间。

图中的方案就是根据贪婪算法得到的最优的解决方案，可以看到每个CPU按照最短的完成时间来进行任务分配。

3） 最快完成时间

针对上面的多线程任务问题，这里假设我们变更要求，要得到最快完成时间，即求所有任务完成需要的时间。

可以得到下面的最优结果

其实这个问题是一个NP-Complete问题，利用贪婪算法很难得到一个最优的结果。这里只是因为例子较少，所以我们可以得到最优结果，但是当例子个数增加时，很难得到结果的。

当然对于这一问题，贪婪算法提供了解决方案，但是解决方案并不是最优的。下面我们来看看这一解决方案

4） 集装箱问题

我们通过一个集装箱问题来介绍贪婪算法在上面问题的解决方案。

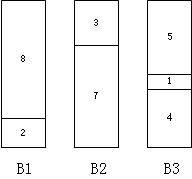
假设我们有一些包裹，他们的大小分别为2,5,4,7,1,4,8 。我们有N个箱子，每个箱子的大小为10，那么问题是要装下这些包裹需要多少个箱子。

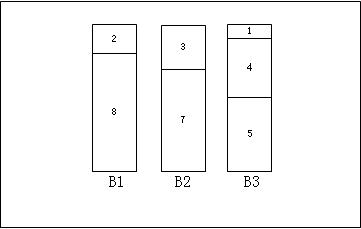
我们可以通过观察得到下面的装箱结果：

可惜计算机不是人类，同时当包裹的数量增长到一定量时，我们也很难通过观察在较短时间内得到结果。因此我们要找到较好的算法解决这一问题。

对于这一问题，有两种情况，一种是on-line的情形，一种是off-line的情形。

a） on-line算法

on-line算法是指来一个包裹我们就要处理一个包裹，我们没法得知后面的包裹的信息。

对于on-line算法，是没有最优算法的。对于on-line算法，一般有3中解决方案

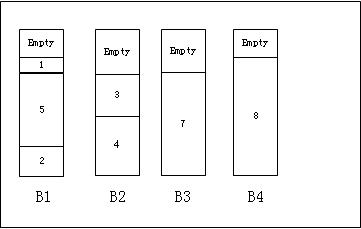
aa）Next-Fit

思想是：对于每一个包裹，如果现在的箱子放不下了，那么就放到一个新的箱子里。

结果如下图所示，我们可以看到这个结果相当不优。

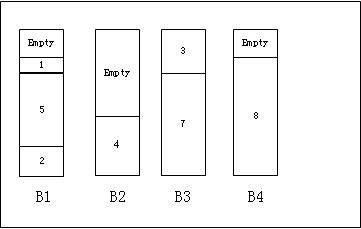
bb）First-Fit

思想是：对于每一个包裹，搜索前面的箱子，把包裹放到第一个能够容纳的箱子里，如果现有的所有箱子都放不下了，那么就放到一个新的箱子里。

结果如下所示，较Next-Fit算法，效果更好一点。

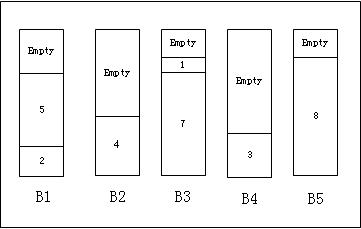
cc）Best-Fit

思想是：对于每一个包裹，搜索前面的箱子，把包裹放到能够最紧凑的容纳的箱子里，如果现有的所有箱子都放不下了，那么就放到一个新的箱子里。

结果如下所示，Best-Fit可以得到更加紧凑的结果。这也应该是on-line算法的最佳选择。

b） off-line算法

off-line算法是指来我们可以在处理包裹前看到所有的包裹信息，然后在对其处理。

我们可以用穷举法得到最优的方案，但是那样太过耗时，尤其是当包裹量很大时，因此我们需要更好地的算法。

这里我们可以首先按照包裹的大小排序，然后再应用上面的First-Fit或者Best-Fit算法。

在实际中First-Fit一般能够取得很好的效果，对上面的例子，可以得到