纠删码(EC)的学习
1. 简介
纠删码(erasure coding,EC)是一种数据保护方法,它将数据分割成片段,把冗余数据块扩展、编码,并将其存储在不同的位置,比如磁盘、存储节点或者其它地理位置。
副本策略和纠删码是存储领域常见的两种数据冗余技术。相比于副本策略,纠删码具有更高的磁盘利用率。 Reed-Solomon码是一种常见的纠删码。
多副本策略即将数据存储多个副本(一般是三副本,比如HDFS),当某个副本丢失时,可以通过其他副本复制回来。三副本的磁盘利用率为1/3。
纠删码技术主要是通过纠删码算法将原始的数据进行编码得到冗余,并将数据和冗余一并存储起来,以达到容错的目的。其基本思想是将n块原始的数据元素通过一定的计算,得到m块冗余元素(校验块)。对于这n+m块的元素,当其中任意的m块元素出错(包括原始数据和冗余数据)时,均可以通过对应的重构算法恢复出原来的n块数据。生成校验的过程被成为编码(encoding),恢复丢失数据块的过程被称为解码(decoding)。磁盘利用率为n/(n+m)。基于纠删码的方法与多副本方法相比具有冗余度低、磁盘利用率高等优点。
多副本策略即将数据存储多个副本(一般是三副本,比如HDFS),当某个副本丢失时,可以通过其他副本复制回来。三副本的磁盘利用率为1/3。
纠删码技术主要是通过纠删码算法将原始的数据进行编码得到冗余,并将数据和冗余一并存储起来,以达到容错的目的。其基本思想是将n块原始的数据元素通过一定的计算,得到m块冗余元素(校验块)。对于这n+m块的元素,当其中任意的m块元素出错(包括原始数据和冗余数据)时,均可以通过对应的重构算法恢复出原来的n块数据。生成校验的过程被成为编码(encoding),恢复丢失数据块的过程被称为解码(decoding)。磁盘利用率为n/(n+m)。基于纠删码的方法与多副本方法相比具有冗余度低、磁盘利用率高等优点。
下图简单阐述了纠删码原理:D1…D10 这10个数据块(甚至可以理解为单个磁盘),P1、P2、P3、P4是对这10个数据块计算出来的纠删码块,这14个块分布在不同的server磁盘上。

根据10个数据块算出4个校验块,即可以容忍任意4个Block的丢失
存储开销: 1.4x = 14/10
任意一个块损坏,需要通过网络读取10个Block进行恢复
纠删码相对于之前多副本的区别:
存储空间降低 :原来3副本需要3倍空间存储一份数据,纠删码只需要1.4倍空间存储一份数据。
可靠性:3副本允许坏的副本数:2/3; 纠删码允许坏的副本数:4/14
额外负担:
计算量(只要有一个坏盘就得通过网络读出n倍的数据并重新计算)
数倍的网络负载
2. 算法核心
下面重点讲一讲Reed-Solomon(RS)码:
Reed-Solomon(RS)码是存储系统较为常用的一种纠删码,它有两个参数n和m,记为RS(n,m)。n代表原始数据块个数。m代表校验块个数。接下来介绍RS码的原理。
RS码原理
以n=5,m=3为例。即5个原始数据块,乘上一个(n+m)*n的矩阵,然后得出一个(n+m)*1的矩阵。根据矩阵特点可以得知结果矩阵中前面5个值与原来的5个数据块的值相等,而最后3个则是计算出来的校验块。
RS码原理
以n=5,m=3为例。即5个原始数据块,乘上一个(n+m)*n的矩阵,然后得出一个(n+m)*1的矩阵。根据矩阵特点可以得知结果矩阵中前面5个值与原来的5个数据块的值相等,而最后3个则是计算出来的校验块。
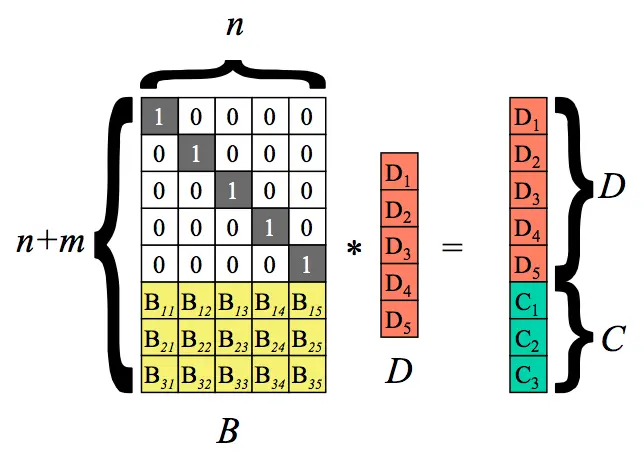
以上过程为编码过程。D是原始数据块,得到的C为校验块。假设丢失了m块数据。如下:
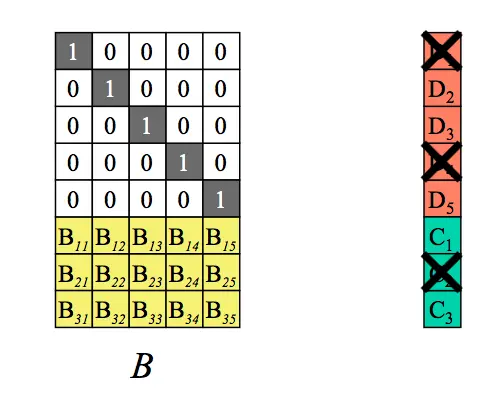
那我们如何从剩余的n个数据块(注意,这里剩余的n块可能包含几个原始数据块+几个校验块)恢复出来原始的n个数据块呢,就需要通过下面的decoding(解码)过程来实现。
第一步:从编码矩阵中删去丢失数据块和丢失编码块对应行。 将删掉m个块的(n+m)*1个矩阵变形为n*1矩阵,同时B矩阵也需要删掉对应的m个行得出一个B'的变形矩阵,这个B'就是n*n矩阵。如下:假设D1、D4、C2丢失,我们得到如下B’矩阵及等式。

第二步:求出B’的逆矩阵。

第三步:等式两边分别乘上B’的逆矩阵。
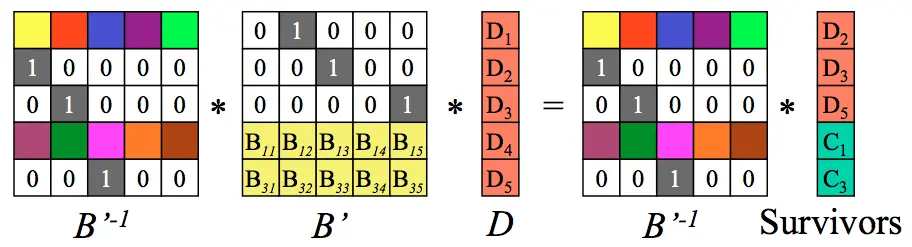
B’和它的逆矩阵相乘得到单位矩阵I,如下:

左边只剩下原始数据矩阵D:
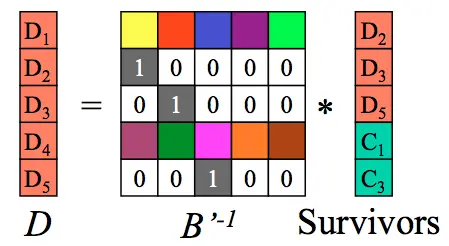
至此完成解码过程。
注:图中黄色部分为范德蒙矩阵。至于如何生成B矩阵,以及如何求B’的逆矩阵,请查看其他相关文献。
3. 参考资料
1. 《Erasure Codes for Storage Applications》
2. 纠删码(Erasure Code)浅析:http://www.jianshu.com/p/4abf65ad03af
2. 纠删码(Erasure Code)浅析:http://www.jianshu.com/p/4abf65ad03af





 本文介绍了纠删码(EC)的基本概念及其与副本策略的区别,着重解析了Reed-Solomon码的工作原理,包括编码与解码过程。通过实例演示了如何通过冗余数据块提高数据的可靠性和磁盘利用率。
本文介绍了纠删码(EC)的基本概念及其与副本策略的区别,着重解析了Reed-Solomon码的工作原理,包括编码与解码过程。通过实例演示了如何通过冗余数据块提高数据的可靠性和磁盘利用率。
















 1203
1203

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








