1 概念
1.1 二叉树概念
二叉树是一种非常重要的数据结构,它同时具有数组和链表各自的特点:它可以像数组一样快速查找,也可以像链表一样快速添加。但是他也有自己的缺点:删除操作复杂。
1.2 二叉树分类
(1) 二叉树:二叉树(binary tree)是一棵树是每个结点最多有两个子树的有序树,在使用二叉树的时候,数据并不是随便插入到节点中的。
(2) 完全二叉树:若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树,如下图
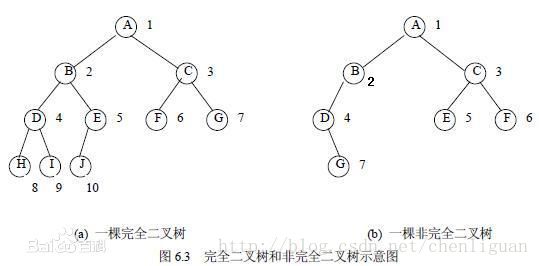
(3) 满二叉树:除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树,如下图
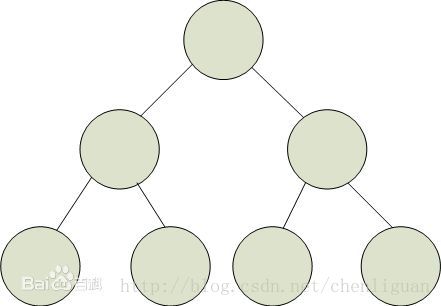
(4)哈夫曼树:哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。下面用一幅图来说明:图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)。

// 它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=481.3 二叉树的特点总结:
- 树执行查找、删除、插入的时间复杂度都是O(logN);
- 遍历二叉树的方法包括前序、中序、后序;
- 非平衡树指的是根的左右两边的子节点的数量不一致;
- 在非空二叉树中,第i层的结点总数不超过 , i>=1;
- 深度为h的二叉树最多有个结点(h>=1),最少有h个结点;
- 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1。
2 哈夫曼树
2.1 如何构建哈夫曼树
2.1.1 一般可以按下面步骤构建
(1)将所有左,右子树都为空的作为根节点。
(2)在森林中选出两棵根节点的权值最小的树作为一棵新树的左,右子树,且
置新树的附加根节点的权值为其左,右子树上根节点的权值之和。
注意,左子树的权值应小于右子树的权值。
(3)从森林中删除这两棵树,同时把新树加入到森林中。
(4)重复2,3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
2.1.2 下面是构建哈夫曼树的图解过程

2.2 哈夫曼(Huffman)编码
利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
就拿上图例子来说:A,B,C,D对应的哈夫曼编码分别为:111,10,110,0,用图说明如下:

注意:设计电文总长最短的二进制前缀编码,就是以n个字符出现的频率作为权构造一棵哈夫曼树,由哈夫曼树求得的编码就是哈夫曼编码。
2.3 应用
为使不等长编码为前缀编码(即要求一个字符的编码不能是另一个字符编码的前缀),可用字符集中的每个字符作为叶子结点生成一棵编码二叉树,为了获得传送报文的最短长度,可将每个字符的出现频率作为字符结点的权值赋予该结点上,显然字使用频率越小权值越小,权值越小叶子就越靠下,于是频率小编码长,频率高编码短,这样就保证了此树的最小带权路径长度效果上就是传送报文的最短长度。因此,求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点,由字符出现频率作为其权值所产生的哈夫曼树的问题。利用哈夫曼树来设计二进制的前缀编码,既满足前缀编码的条件,又保证报文编码总长最短。
3 图例演示
3.1 二叉树

3.2 二叉树的遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。二叉树的遍历方式有很多,主要有:前序遍历,中序遍历,后序遍历。
(1)前序遍历:若二叉树为空,则空操作返回;否则根左右:先访问根节点,然后前序遍历左子树,再前序遍历右子树。

(2)中序遍历:若树为空,则空操作返回;否则左根右:从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树。可以看到,如果是二叉排序树,中序遍历的结果就是个有序序列。

(3)后序遍历:若树为空,则空操作返回;否则左右根先遍历左子树,再遍历右子树,最后访问根结点。在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。

图片来源于:数据结构(二)之二叉树
4 二叉树遍历源码
package Tree;
public class BinaryTree {
private TreeNode root = null;
public static String[] str;
public static int count;
public BinaryTree() {
root = new TreeNode(1, "A");
}
/**
* 构建二叉树 A B C D E F
*/
public void createBinaryTree() {
TreeNode nodeB = new TreeNode(2, "B");
TreeNode nodeC = new TreeNode(3, "C");
TreeNode nodeD = new TreeNode(4, "D");
TreeNode nodeE = new TreeNode(5, "E");
TreeNode nodeF = new TreeNode(6, "F");
root.leftChild = nodeB;
root.rightChild = nodeC;
nodeB.leftChild = nodeD;
nodeB.rightChild = nodeE;
nodeC.rightChild = nodeF;
}
/**
* 根据前序序列递归构建二叉树
*/
public TreeNode createBinaryTree(ArrayList<String> data) {
return createBinaryTree(data.size(),data);
}
public TreeNode createBinaryTree(int size, ArrayList<String> data) {
if (data.size() == 0) {
return null;
}
String d = data.get(0);
TreeNode node = null;
int index = size - data.size();//获取节点下标
if (d.equals("#")) {
node = null;
data.remove(0);// 删除“#”
return node;//退出
}
node = new TreeNode(index, d);// 创建新节点
if (index == 0) {
root = node;// 创建根节点
}
data.remove(0);
node.leftChild = createBinaryTree(size, data);
node.rightChild = createBinaryTree(size, data);
return node;
}
/**
* 求二叉树的高度
*/
public int getHeight() {
return getHeight(root);
}
private int getHeight(TreeNode node) {
if (node == null) {
return 0;
} else {
int i = getHeight(node.leftChild);
int j = getHeight(node.rightChild);
return (i < j) ? j + 1 : i + 1;
}
}
/**
* 获取二叉树的结点数
*/
public int getSize() {
return getSize(root);
}
private int getSize(TreeNode node) {
if (node == null) {
return 0;
} else {
return 1 + getSize(node.leftChild) + getSize(node.rightChild);
}
}
/**
* 前序遍历——迭代
*
* 规则是若二叉树为空,则空操作返回;否则先访问根结点,然后前序遍历左子树,再前序遍历右子树(根左右)
*/
public void preOrder(TreeNode node) {
if (node == null) {
return;
} else {
System.out.println("前序遍历——迭代:" + node.getData());
preOrder(node.leftChild);
preOrder(node.rightChild);
}
}
/**
* 中序遍历——迭代
*
* 规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树(左根右)
*/
public void midOrder(TreeNode node) {
if (node == null) {
return;
} else {
midOrder(node.leftChild);
System.out.println("中序遍历——迭代:" + node.getData());
midOrder(node.rightChild);
}
}
/**
* 后序遍历——迭代
*
* 规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点(左到右先叶子后结点)
*/
public void postOrder(TreeNode node) {
if (node == null) {
return;
} else {
postOrder(node.leftChild);
postOrder(node.rightChild);
System.out.println("后序遍历——迭代:" + node.getData());
}
}
/**
* 前序遍历——非迭代
*/
public void theFirstTraversal_Stack(TreeNode root) { // 先序遍历
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode node = root;
while (node != null || stack.size() > 0) { // 将所有左孩子压栈
if (node != null) { // 压栈之前先访问
System.out.println("前序遍历——非迭代:" + node.getData());
stack.push(node);
node = node.leftChild;
} else {
node = stack.pop();
node = node.rightChild;
}
}
}
/**
* 中序遍历——非迭代
*/
public void theInOrderTraversal_Stack(TreeNode root) { // 中序遍历
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode node = root;
while (node != null || stack.size() > 0) {
if (node != null) {
stack.push(node); // 直接压栈
node = node.leftChild;
} else {
node = stack.pop(); // 出栈并访问
System.out.println("中序遍历——非迭代:" + node.getData());
node = node.rightChild;
}
}
}
/**
* 后序遍历——非迭代
*/
public void thePostOrderTraversal_Stack(TreeNode root) { // 后序遍历
Stack<TreeNode> stack = new Stack<TreeNode>();
Stack<TreeNode> output = new Stack<TreeNode>();// 构造一个中间栈来存储逆后序遍历的结果
TreeNode node = root;
while (node != null || stack.size() > 0) {
if (node != null) {
output.push(node);
stack.push(node);
node = node.rightChild;// 遍历右子树
} else {
node = stack.pop();
node = node.leftChild;// 遍历左子树
}
}
while (output.size() > 0) {
System.out.println("后序遍历——非迭代:" + output.pop().getData());
}
}
public class TreeNode {
private int index;
private String data;
private TreeNode leftChild;
private TreeNode rightChild;
private TreeNode parent;
public int getIndex() {
return index;
}
public void setIndex(int index) {
this.index = index;
}
public String getData() {
return data;
}
public void setData(String data) {
this.data = data;
}
public TreeNode getLeftChild() {
return leftChild;
}
public void setLeftChild(TreeNode leftChild) {
this.leftChild = leftChild;
}
public TreeNode getRightChild() {
return rightChild;
}
public void setRightChild(TreeNode rightChild) {
this.rightChild = rightChild;
}
public TreeNode getParent() {
return parent;
}
public void setParent(TreeNode parent) {
this.parent = parent;
}
public TreeNode(int index, String data) {
this.index = index;
this.data = data;
this.leftChild = null;
this.rightChild = null;
}
}
public static void main(String[] args) {
// BinaryTree binaryTree = new BinaryTree();
// binaryTree.createBinaryTree();
ArrayList<String> data = new ArrayList<>();
String[] dataArray = new String[]{"A","B","D","#","#","E","#","#","C","#","F","#","#"};
for(String d:dataArray){
data.add(d);
}
BinaryTree binaryTree = new BinaryTree();
binaryTree.createBinaryTree(data);//创建二叉树
int height = binaryTree.getHeight();//求二叉树的高度
System.out.println("treeHeihgt:" + height);
int size = binaryTree.getSize();//获取二叉树的结点数
System.out.println("treeSize:" + size);
// binaryTree.preOrder(binaryTree.root);//前序遍历-迭代
// binaryTree.midOrder(binaryTree.root);//中序遍历-迭代
// binaryTree.postOrder(binaryTree.root);//后序遍历-迭代
binaryTree.theFirstTraversal_Stack(binaryTree.root);// 前序遍历-非迭代
System.out.println("\n");
binaryTree.theInOrderTraversal_Stack(binaryTree.root);// 中序遍历-非迭代
System.out.println("\n");
binaryTree.thePostOrderTraversal_Stack(binaryTree.root);// 后序遍历-非迭代
}
}





















 2296
2296

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








