所有图片均可 右击|在新标签页中打开,然后放大查看
不保证答案正确性,欢迎同学评论斧正

 1.
1.
分析:既然正常机器人总能答对题,故障机器人反之,那就每个机器人问一个事先知道答案的问题好了。
 2.
2.

答案:40 8。
分析:myArray数组存放的单个元素大小为4 byte,故整个数组尺寸为40字节。C语言中,数组传参会退化为指针,它代表着内存地址,由于是64位的环境,所以该指针为8字节。
 3.
3.
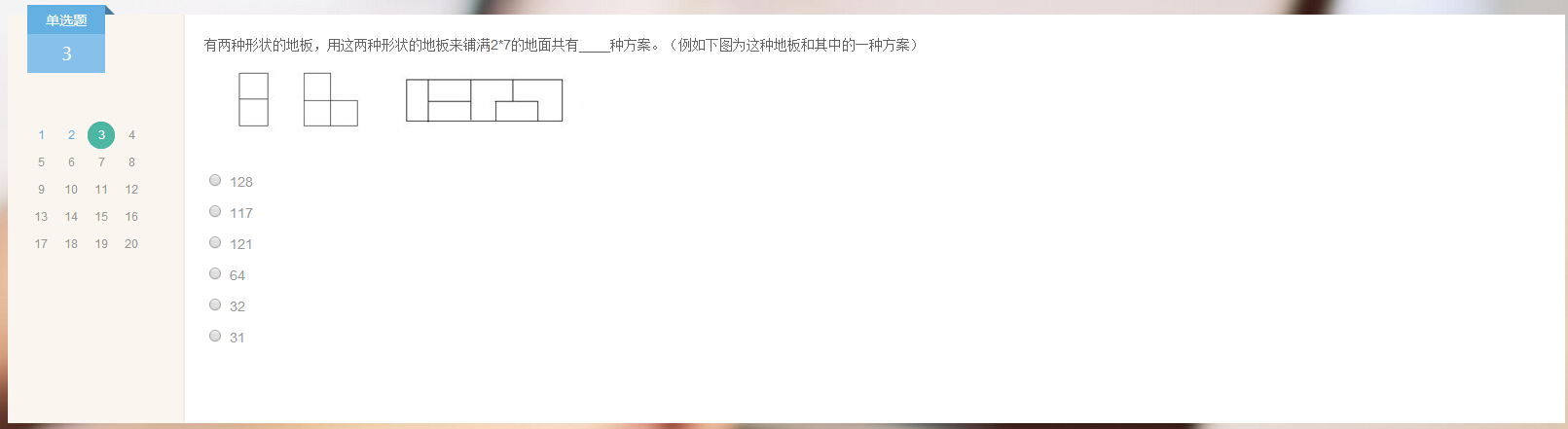
状态压缩:用int型数据保存拼图过程中的图案。二进制表示的倒数第i位表示2*7地面中第i个格子是否被地板铺上与否。
动态规划:dp[r][c][sta]表示在形状sta的基础上,在(r,c)位置开始拼,拼满整个地面的情况种类数目。那么状态转移方程就是:
if (c + 1 < COLUMN)
dp[r][c][sta] += DP(r, c + 1, staTemp);
else
dp[r][c][sta] += DP(r + 1, 0, staTemp);//staTemp表示铺上某块地板后的新图案。记忆化搜索:已计算过的不要重复计算,不然开销大到不能承受。
结构体设计:有Point与Shape,后者表示砖的形状。因为每块砖的面积都大于1*1,所以我们可以缺省一个,省点代码量。见下图:

/**
* 单选第三题
* 状态压缩+动态规划+记忆化搜索
*/
import java.util.ArrayList;
import java.util.List;
import static java.lang.System.out;
//r为行序,c为列序,从上到下,从左到右,都从0开始
//( (stat >> (r * COLUMN + c) ) & 1 ) 表示r行c列是否被地板覆盖——————1表示覆盖;0表示未覆盖。
class Point {
int x, y;
public Point(int a, int b) {
x = a;
y = b;
}
}
class Shape {
List
p;
}
public class A {
boolean DEBUG=true;
final int ROW = 2, COLUMN = 7;
final int FULL = (1 << ROW * COLUMN) - 1;
int[][][] dp = new int[ROW][COLUMN][1 << (ROW * COLUMN + 1)];
boolean[][][] vis = new boolean[ROW][COLUMN][1 << (ROW * COLUMN + 1)];
/** 地板可以旋转,总共六种形状 */
Shape[] SH = new Shape[6];
public static void main(String[] args) {
A obj = new A();
obj.initial();
int ans = obj.DP(0, 0, 0);
out.println("ANS:" + ans);
}
/** 表示尝试过程中合理的情况 */
void debug(boolean isDebug, int sta, int staTemp) {
if(!isDebug)
return;
show(sta);
out.println("--->");
show(staTemp);
out.println();
}
void initial() {
for (int i = 0; i < SH.length; i++) {
SH[i] = new Shape();
SH[i].p = new ArrayList
();
}
SH[0].p.add(new Point(0, 1));
SH[1].p.add(new Point(1, 0));
SH[2].p.add(new Point(0, 1));
SH[2].p.add(new Point(1, 1));
SH[3].p.add(new Point(1, 1));
SH[3].p.add(new Point(1, 0));
SH[4].p.add(new Point(1, 0));
SH[4].p.add(new Point(1, -1));
SH[5].p.add(new Point(1, 0));
SH[5].p.add(new Point(0, 1));
}
/** 图形化输出sta状态表示的图案 */
void show(int sta) {
for (int i = 0; i < ROW * COLUMN; i++) {
if (i == COLUMN)
out.println();
out.print(sta & 1);
sta >>= 1;
}
out.println();
}
/** 返回值表示——————在形状sta的基础上,在(r,c)位置开始拼,拼满整个地面的情况种类 */
int DP(int r, int c, int sta) {
// 如果全铺满
if (sta == FULL)
return 1;
// 如果越界
if (r >= ROW || r < 0 || c >= COLUMN || c < 0)
return 0;
// 记忆化搜索
if (vis[r][c][sta])
return dp[r][c][sta];
vis[r][c][sta] = true;
boolean isRecovered = ((sta >> (r * COLUMN + c)) & 1) == 1;
if (!isRecovered) {
// 6种形状的地板
for (int i = 0; i < 6; i++) {
boolean flag = true;
// 每种形状的地板都有1*1的部分是默认放在(r,c)位置的
int staTemp = sta + (1 << (r * COLUMN + c));
for (int j = 0; j < SH[i].p.size(); j++) {
int pos = (SH[i].p.get(j).x + r) * COLUMN
+ SH[i].p.get(j).y + c;
if (SH[i].p.get(j).x + r < 0 || SH[i].p.get(j).x + r >= ROW
|| SH[i].p.get(j).y + c < 0
|| SH[i].p.get(j).y + c >= COLUMN ||
// 这个位置已经被其他地板覆盖
((staTemp >> pos) & 1) == 1) {
flag = false;
break;
}
staTemp += (1 << pos);
}// for-每块木板的多个单位
// 如果该块木板可以放下,代入状态转移方程
if (flag) {
debug(DEBUG, sta, staTemp);
// 同行从左往右放,放满了再起一行从第0列放
if (c + 1 < COLUMN)
dp[r][c][sta] += DP(r, c + 1, staTemp);
else
dp[r][c][sta] += DP(r + 1, 0, staTemp);
}
}// for-铺不同的木板
} else
// 此处不能放继续尝试,原图形状态sta保持不变
{
if (c + 1 < COLUMN)
dp[r][c][sta] += DP(r, c + 1, sta);
else
dp[r][c][sta] += DP(r + 1, 0, sta);
}
return dp[r][c][sta];
}
}
//ANS:117
 4.
4.

这道题没什么价值。
模式识别,Pattern Recognition,就是通过计算机用数学技术方法来研究模式的自动处理和判读,模拟生命体对环境及客体的识别。比如你的同桌小明今天换了一套衣服,你仍然能认出来;商店里有形形状状的笔,你都能知道它们还是笔。
对人类来说,特别重要的是对光学信息(通过视觉器官来获得)和声学信息(通过听觉器官来获得)的识别。这是模式识别的两个重要方面。
 5.
5.
答案:以上描述都对。
 6.
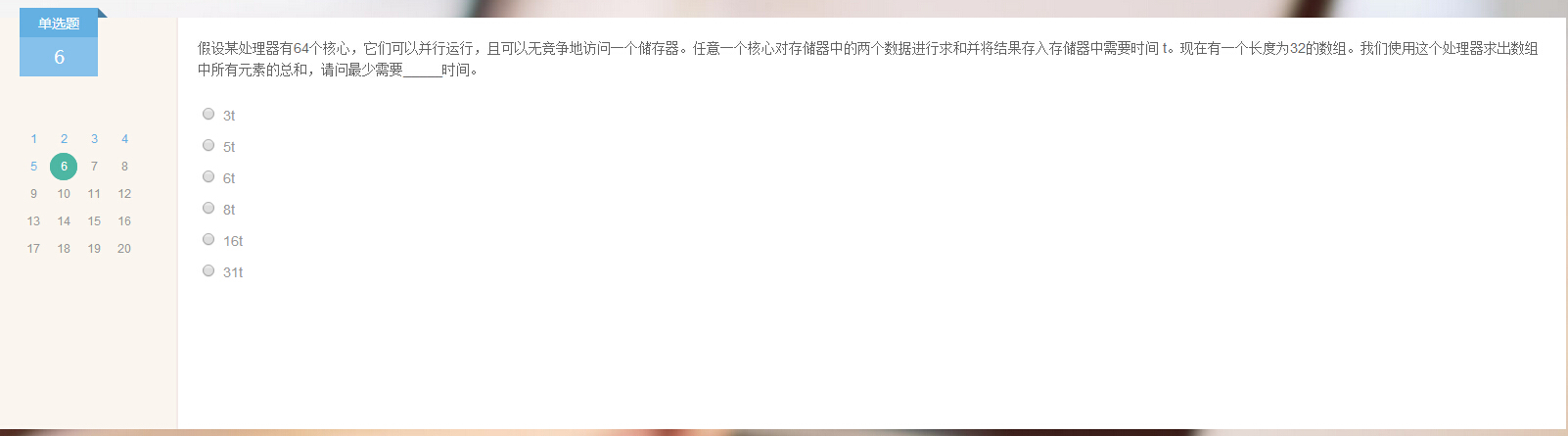
6.
答案:5t。
分析:64个核心足够用,第一次对32个元素两两分组,花费t时间得到16个和;第二次对上一步得到的16个元素两两分组,花费t时间得到8个和;...;以此类推,5t时间可得到最终结果。
 7.
7.
/**
* 单选第7题
* @author yc_du
*/
public class Dice {
//设置result数组是必要的,不然会有 非常非常大量 的重复计算
static double []result=new double[2016];
public static void main(String[] args) {
//设置边界值
result[1]=1.0/6;
System.out.println(fun(2015));
}
static double fun(int x){
if(x<=0)
return 0;
else{
if(result[x]==0){
result[x]=fun(x-1)/6+fun(x-2)/6+fun(x-3)/6+fun(x-4)/6+fun(x-5)/6+fun(x-6)/6;
//如果点数在[1,6]范围内,可以一次得到
if(x<=6)
result[x]+=1.0/6;
}
return result[x];
}
}
}
//fun(2): 7/36=0.194
//fun(3): 1/(6^3)+2/(6^2)+1/6=49/(6^3)= 0.22685
//fun(2015): 0.2857142857142857 约等于 2/7
 8.
8.

 9.
9.

传统的暴力匹配未能利用已匹配部分的信息,效率低下。KMP的核心在于构造状态转换图,可用失配函数表示。
详见 http://blog.csdn.net/chuchus/article/details/29910345
希尔排序
算法先将要排序的一组数按某个增量d分成若干组,每组中记录的下标相差d.对每组中全部元素进行排序,然后再用一个较小的增量对它进行,在每组中再进行排序。当增量减到1时,整个要排序的数被分成一组,排序完成。
冒泡排序
太常见了。
Dijkstra算法
Dijkstra挺厉害的,现在我们很难想象如果函数不能递归该是多么地不方便。而Dijkstra就是当时力排非议引入递归编程思想的。
求最短路算法的思想见下:
原图为G=(V,E),求s到任意顶点的最短路径。辅助数组dist[i]表示当前从源点s到顶点i的最短路径,辅助数组visited[ ]表示集合A。
1.初始化,置dist[i]=graph[s][i],A中只有s点。
2.找到具有最小值的dist[x],x属于V-A。x加入A,更新所有的dist[ y ],y属于V-A。更新步骤为 if(dist[x]+graph[x][y]<dist[y]) { dist [ y ]=dist[x]+graph[ x ] [ y ] ; }
3.不断重复步骤2 ,直至V=A。
快速排序
嵌套加递归的排序思想。最坏时间复杂度 O(n*n),平均复杂度O(n*log(底数:2)(真数:n))
详见http://blog.csdn.net/chuchus/article/details/21822557
floyd算法
不同于Dijkstra算法的另一种最短路算法,是一个经典的动态规划算法。
它是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,时间复杂度为O(N^3),空间复杂度为O(N^2)。
贪心的主要思想就是用局部的最优解去逼近或达到总体的最优解。Dijkstra算法中的 if(dist[x]+graph[x][y]<dist[y]) { dist [ y ]=dist[x]+graph[ x ] [ y ] ; }思想就属于贪心。
 10.
10.

string在解释时是以\0作为结束标志的。但人为存放内容的时候还是可以放多个\0的。
 11.
11.
我们先从反面计算强队不与强队碰面的情况。那么ABCD每组内都是一强一弱。令,每队的1号比2号强,那么总排列数是num1=4*4*3*3*2*2*1*1。又因为2号比1号强也可以,考虑次序总排列数是num2=num1*2*2*2*2。
所求结果为1-num2/n,为27/35。
 12.
12.

 13.
13.
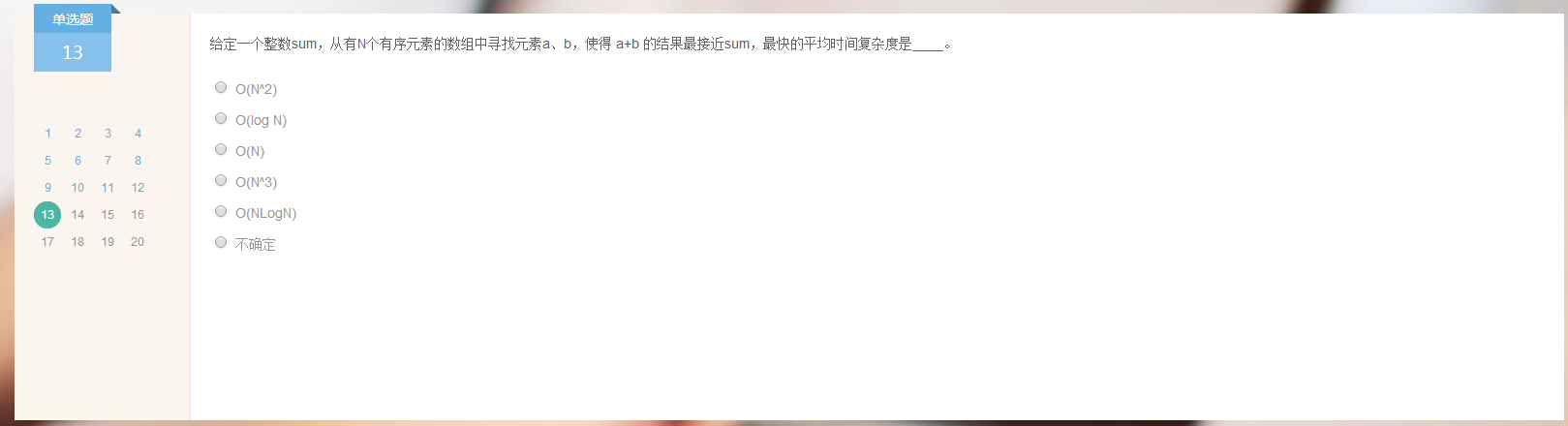
初始时,游标a指向最左端,游标b指向最右端。若两个游标所指的元素和小于给定sum,游标b左移;否则游标a右移。用一个变量存储移动过程中两元素和与sum的历史最小差值。 复杂度n。
综上复杂度还是nlogn。
 14.
14.

分析:对1400分解质因数,1400=2^3*5^2*7。三个质数的指数分别加上1再相乘,即(3+1)*(2+1)*(1+1)=4*3*2=24。故有24个因数(约数个数定理)。题目说把1排除那就剩下23个。
 15.
15.
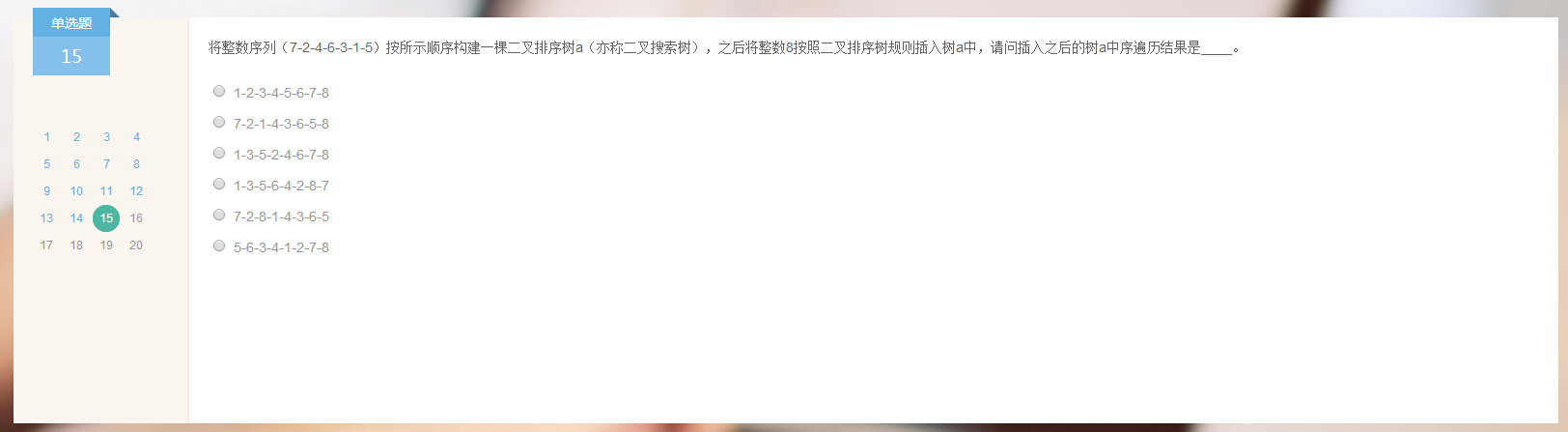
 16.
16.
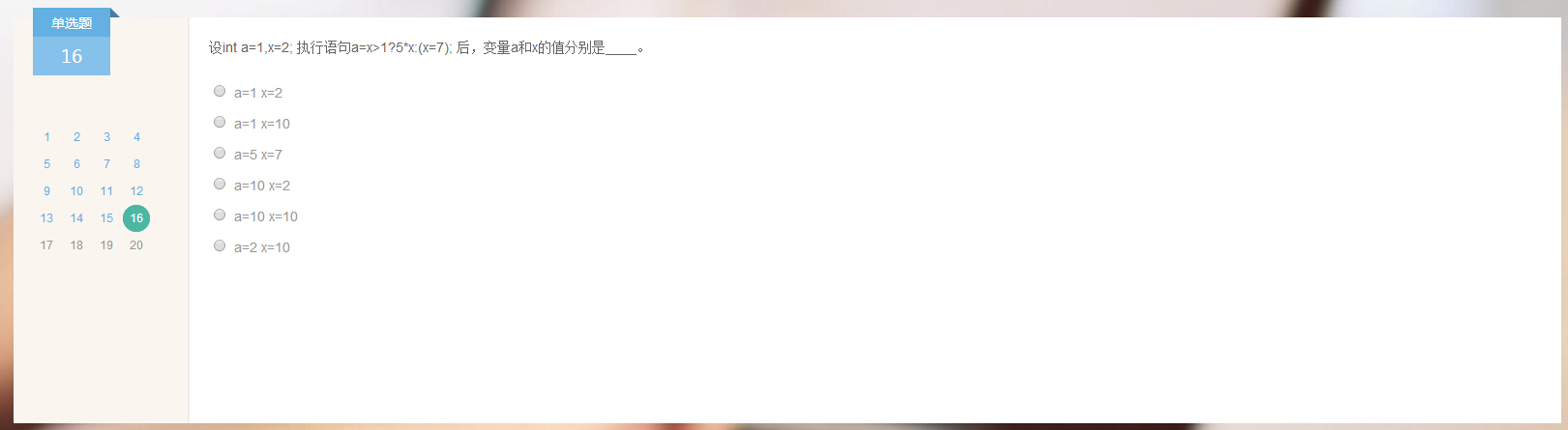
分析:x>1为真,所以执行效果为a=5*x,答案是显然的。
 17.
17.
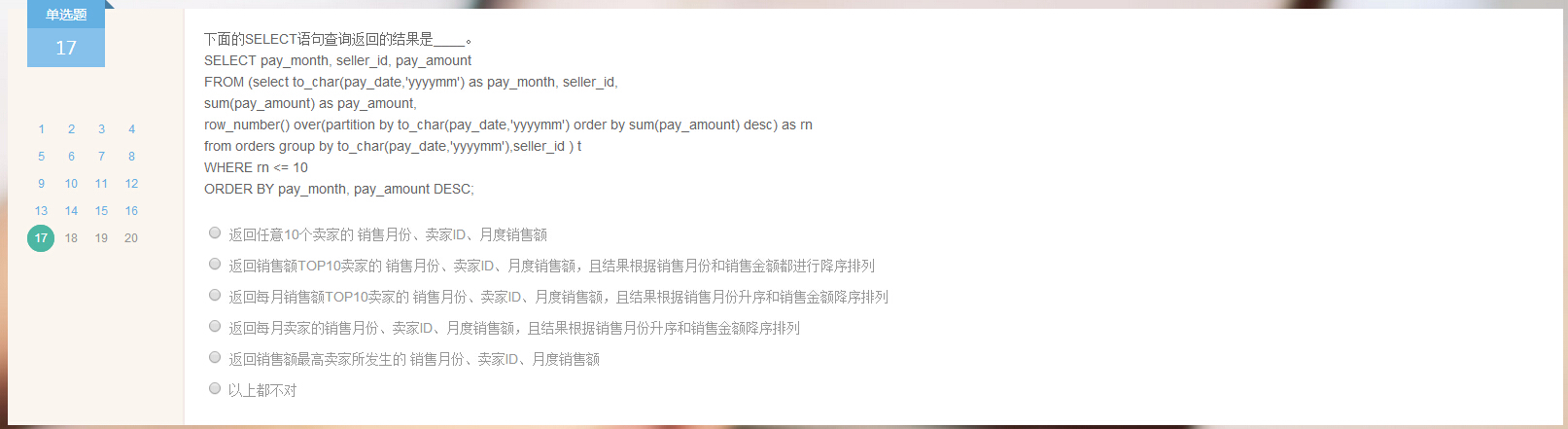
 18.
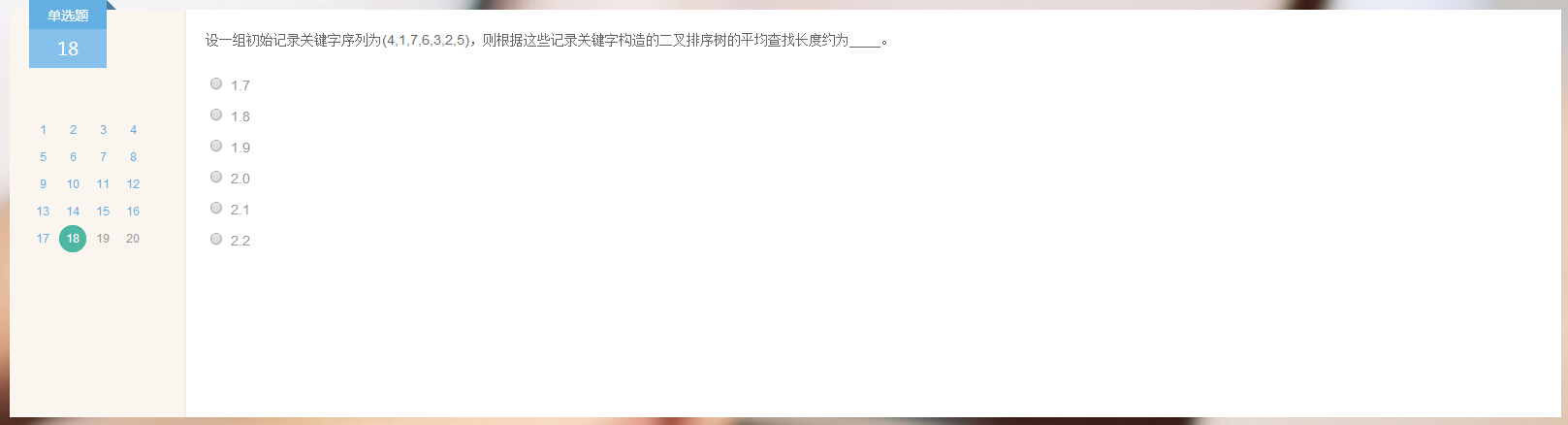
18.
分析: 二叉树见下图:
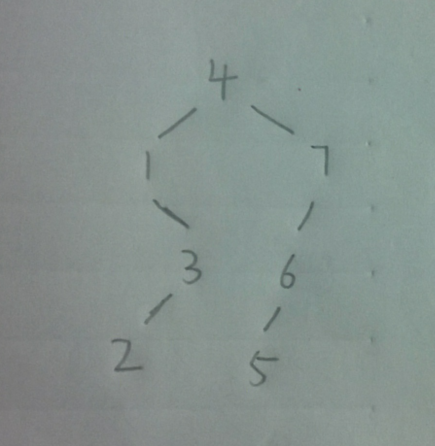
 19.
19.
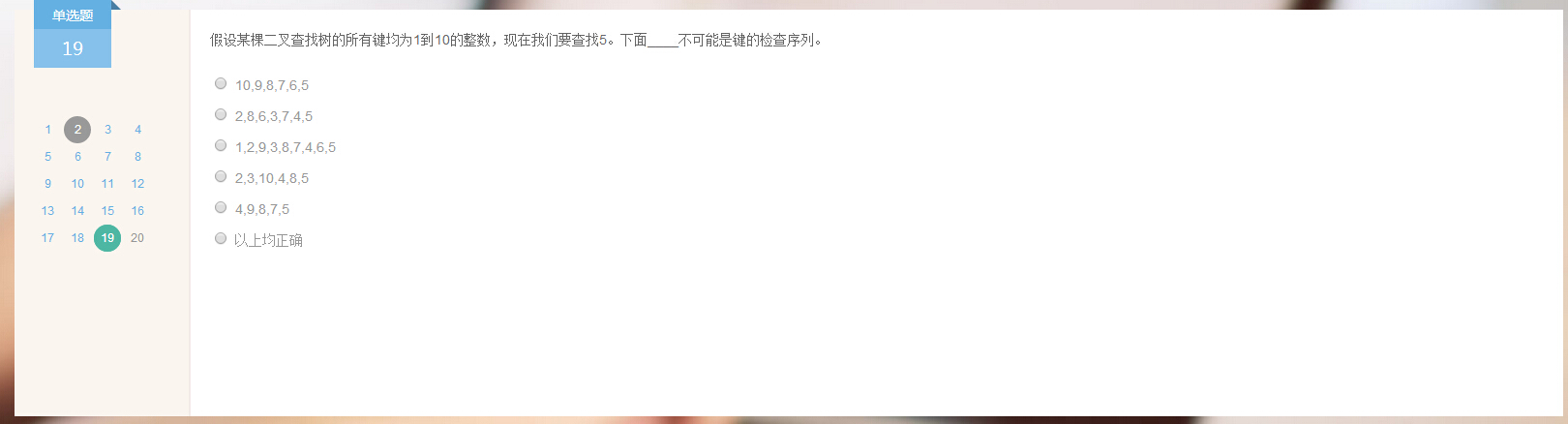
分析:观察它的子序列 6、3、7。6->3说明待查元素比6小,后面就不会再找到7了,所以有误。
 20.
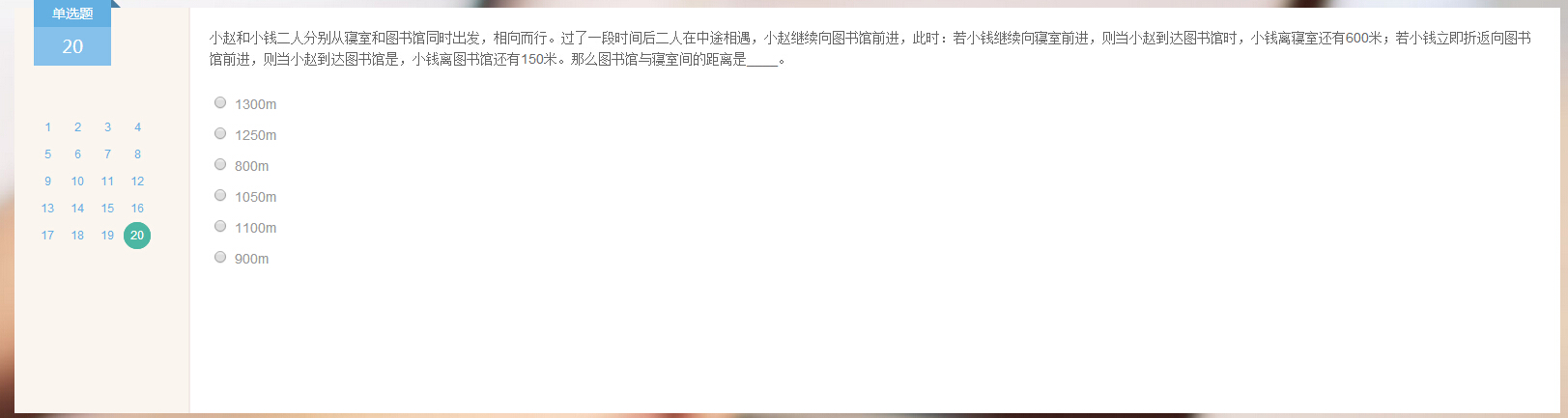
20.
答案:900米。
分析:见下图。
public class AlibabaQuestion20 {
public static void main(String[] args) {
double ans=binSearch(1,10000);
System.out.println(ans);
}
static double fun(double s){
double t=s/(s-600);
double x2=t*s-150*(t*t+t);
return s-x2;
}
static double binSearch(double start,double end){
while(start
0是取start=mid呢还是end=mid? 反正只有两种情况,可以尝试
if(tmp>0) start=mid;
else end=mid;
}
return 0;
}
}
/*程序输出899.9999999349238 故900为答案*/
 附加题1
附加题1
答案:见分析。
分析:
//fun()函数返回值 等于 k的概率见 公式附加1.1
int fun(int N){
int result=0;
for(int i=0;i<N;i++)
result+=G();
return result;
}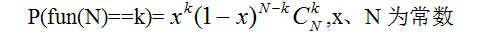 -------------公式附加1.1
-------------公式附加1.1
令公式附加1.1等于p,解出k即可。
解出来的k不是整数怎么办呢?不难办,N越大k就越能够向整数靠拢。
解得k后,即可编写f()函数:
int f(){
return fun(N)==k;
}莱布尼兹级数:pi/4=1-1/3+1/5-1/7+1/9+...
e约等于2.718281828459,级数展开见下图:
 附加题2
附加题2
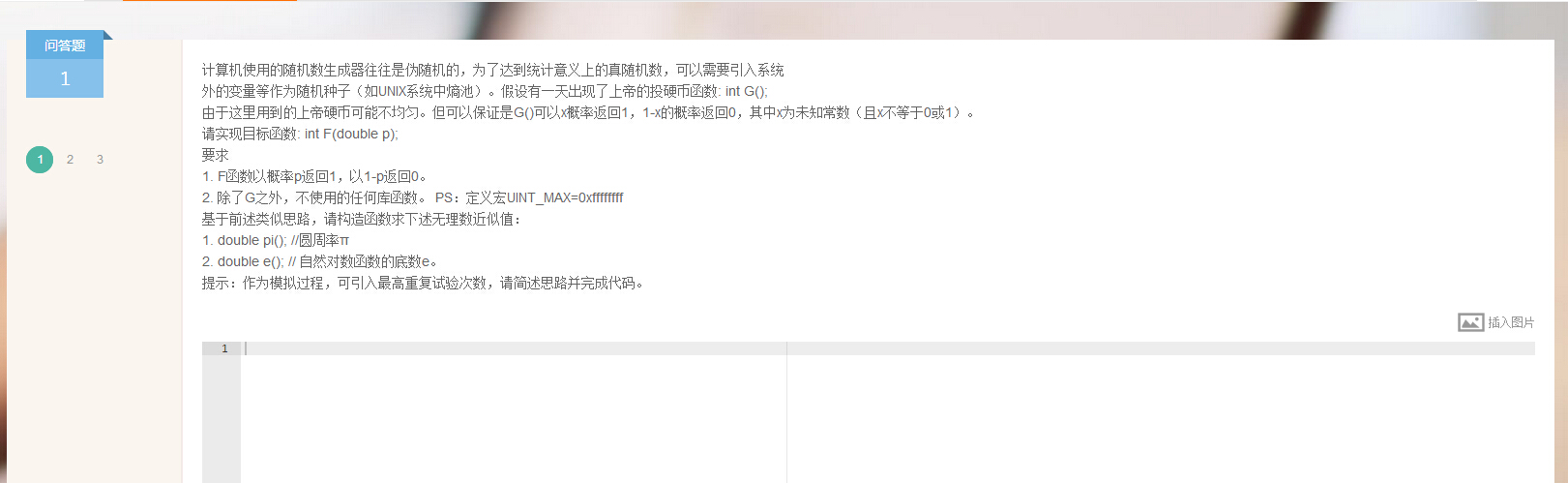
答案:见代码。
/****
* Alibaba附加题第二题
* 时间复杂度:O(2n)
* 空间复杂度:O(2n)
*/
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Set;
class Tuple {
public int data1, data2;
/**是否已被加入到某个group中,没有此标志位无法进行深度优先搜索,除非再来个辅助布尔数组*/
public boolean isUsed;
public Tuple(int a, int b) {
data1 = a;
data2 = b;
}
@Override
public String toString() {
return data1 + "," + data2;
}
}
class Group {
Set
tupleSet = new HashSet
();
Set
elementSet = new HashSet
();
}
public class Calc {
/**程序的输入*/
List
tupleList = new ArrayList
(); /** map.get(i)得到一个Set,Set中存放的所有元组都含有元素i。 */ Map
> map = new HashMap
>(); /**groupList存储各group信息*/ List
groupList = new ArrayList
(); public static void main(String[] args) { Calc obj = new Calc(); obj.init(); obj.initMap(); System.out.println(obj.map); obj.initGroupList(); System.out.println("共有" + obj.groupList.size() + "个group"); int k = 0; for (Group group : obj.groupList) System.out.println("第" + ++k + "个group" + "含有的元素有" + group.elementSet); System.out.println(); } void init() { tupleList.add(new Tuple(1, 8)); tupleList.add(new Tuple(2, 5)); tupleList.add(new Tuple(3, 5)); tupleList.add(new Tuple(8, 4)); tupleList.add(new Tuple(2, 3)); } void initMap() { for (int i = 0; i < tupleList.size(); i++) { int data = tupleList.get(i).data1; Set
set = (Set
) map.get(data); if (set == null) { set = new HashSet
(); map.put(data, set); } set.add(tupleList.get(i)); data = tupleList.get(i).data2; set = (Set
) map.get(data); if (set == null) { set = new HashSet
(); map.put(data, set); } set.add(tupleList.get(i)); } } void initGroupList() { for (int i = 0; i < tupleList.size(); i++) { if (tupleList.get(i).isUsed) continue; Group group = new Group(); groupList.add(group); addToGroup(tupleList.get(i), group); } } /** 拥有相同元素的tuple添加到同一group,递归 */ void addToGroup(Tuple tuple, Group group) { if (tuple.isUsed == true) return; tuple.isUsed = true; group.elementSet.add(tuple.data1); group.elementSet.add(tuple.data2); group.tupleSet.add(tuple); Set
set1 = map.get(tuple.data1); for (Tuple tuple2 : set1) addToGroup(tuple2, group); Set
set2 = map.get(tuple.data2); for (Tuple tuple2 : set2) addToGroup(tuple2, group); } } /* * {1=[1,8], 2=[2,3, 2,5], 3=[3,5, 2,3], 4=[8,4], 5=[3,5, 2,5], 8=[1,8, 8,4]} * 共有2个group 第1个group含有的元素有[1, 4, 8] 第2个group含有的元素有[2, 3, 5] */
时间复杂度:构造map的过程是一次遍历,构造group的时候是一次深度优先搜索,所以总的为O(2n)。
空间复杂度:map的key键集合占据了O(2n)的空间(因为是2元组)。其他List、Set存放的都是引用。
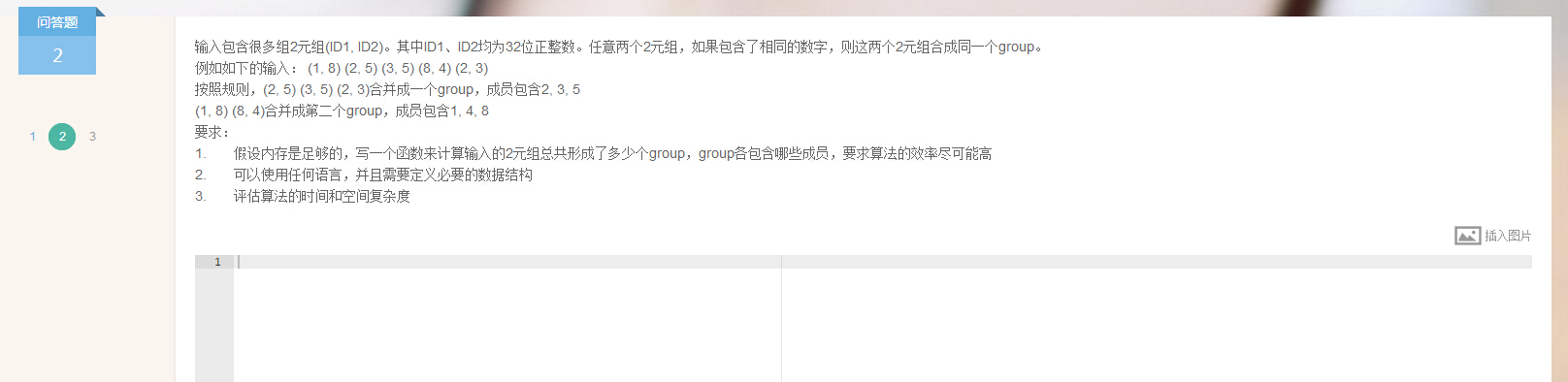
 附加题3
附加题3
这题随便写啦:
1.私有云需要花时间自己搭建,而公有云购买之后可快速部署代码;
2.公有云扩容比较方便;
3.短期来看公有云的成本反而更低。










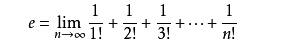















 3626
3626

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








