图像的灰度共生矩阵
灰度共生矩阵是像素距离和角度的矩阵函数,它通过计算图像中一定距离和一定方向的两点灰度之间的相关性,来反映图像在方向、间隔、变化幅度及快慢上的综合信息。
使用方法:
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)
描述:
glcms = graycomatrix(I) 产生图像I的灰度共生矩阵GLCM。它是通过计算两灰度值在图像I中水平相邻的次数而得到的 (也不必是水平相邻的次数,这一参数是可调的,可能通过Offsets来进行调整,比如[0 D]代表是水平方向,[-D D]代表是右上角45度方向,[-D 0]代表是竖直方向,即90度方向,而[-D -D]则代表是左上角,即135度方向),GLCM中的每一个元素(i,j)代表灰度i与灰度j在图像中水平相邻的次数。
因为动态地求取图像的GLCM区间代价过高,我们便首先将灰度值转换到I的灰度区间里。如果I是一个二值图像,那么灰度共生矩阵就将图像转换到两级。如果I是一个灰度图像, 那将转换到8级。灰度的级数决定了GLCM的大小尺寸。你可以通过设定参数“NumLevels”来指定灰度的级数,还可以通过设置“GrayLimits"参数来设置灰度共生矩阵的转换方式。
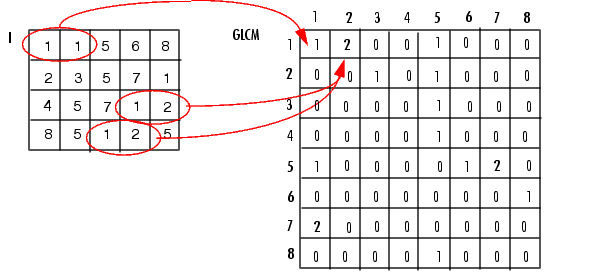
下图显示了如何求解灰度共生矩阵,以(1,1)点为例,GLCM(1,1)值为1说明只有一对灰度为1的像素水平相邻。GLCM(1,2)值为2,是因为有两对灰度为1和2的像素水平相邻。(1,5)出现一次,所以在(1.5)位置上标记1,没出现(1,6)所以为0;
glcms = graycomatrix(I,param1,val1,param2,val2,...) 返回一个或多个灰度灰度共生矩阵,根据指定的参数。参数可以很简短,并且对大小写不敏感。
参数
'GrayLimits' 是两个元素的向量,表示图像中的灰度映射的范围,如果其设为[],灰度共生矩阵将使用图像I的最小及最大灰度值作为GrayLimits
'NumLevels' 一个整数,代表是将图像中的灰度归一范围。举例来说,如果NumLevels为8,意思就是将图像I的灰度映射到1到8之间,它也决定了灰度共生矩阵的大小
'Offset' 上面有解释,是一个p*2的整数矩阵,D代表是当前像素与邻居的距离,通过设置D值,即可设置角度
Angle Offset
0 [0 D]
45 [-D D]
90 [-D 0]
135 [-D -D]
示例:
计算灰度共生矩阵,并且返回缩放后的图像,SI
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,'NumLevels',9,'G',[])
计算灰度图像的灰度共生矩阵
I = imread('circuit.tif');
glcm = graycomatrix(I,'Offset',[2 0]);
灰度共生矩阵的特征:
角二阶矩(Angular Second Moment, ASM)
ASM=sum(p(i,j).^2) p(i,j)指归一后的灰度共生矩阵
角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量,当图像纹理绞细致、灰度分布均匀时,能量值较大,反之,较小。
熵(Entropy, ENT)
ENT=sum(p(i,j)*(-ln(p(i,j)))
是描述图像具有的信息量的度量,表明图像的复杂程序,当复杂程序高时,熵值较大,反之则较小。
反差分矩阵(Inverse Differential Moment, IDM)
IDM=sum(p(i,j)/(1+(i-j)^2))
反映了纹理的清晰程度和规则程度,纹理清晰、规律性较强、易于描述的,值较大;杂乱无章的,难于描述的,值较小。
共生矩阵用两个位置的象素的联合概率密度来定义,它不仅反映亮度的分布特性,也反映具有同样亮度或接近亮度的象素之间的位置分布特性,是有关图象亮度变化的二阶统计特征。它是定义一组纹理特征的基础。
一幅图象的灰度共生矩阵能反映出图象灰度关于方向、相邻间隔、变化幅度的综合信息,它是分析图象的局部模式和它们排列规则的基础。
设f(x,y)为一幅二维数字图象,其大小为M×N,灰度级别为Ng,则满足一定空间关系的灰度共生矩阵为
P(i,j)=#{(x1,y1),(x2,y2)∈M×N|f(x1,y1)=i,f(x2,y2)=j}
其中#(x)表示集合x中的元素个数,显然P为Ng×Ng的矩阵,若(x1,y1)与(x2,y2)间距离为d,两者与坐标横轴的夹角为θ,则可以得到各种间距及角度的灰度共生矩阵P(i,j,d,θ)。
纹理特征提取的一种有效方法是以灰度级的空间相关矩阵即共生矩阵为基础的[7],因为图像中相距(Δx,Δy)的两个灰度像素同时出现的联合频率分布可以用灰度共生矩阵来表示。若将图像的灰度级定为N级,那么共生矩阵为N×N矩阵,可表示为M(Δx,Δy)(h,k),其中位于(h,k)的元素mhk的值表示一个灰度为h而另一个灰度为k的两个相距为(Δx,Δy)的像素对出现的次数。
对粗纹理的区域,其灰度共生矩阵的mhk值较集中于主对角线附近。因为对于粗纹理,像素对趋于具有相同的灰度。而对于细纹理的区域,其灰度共生矩阵中的mhk值则散布在各处。
为了能更直观地以共生矩阵描述纹理状况,从共生矩阵导出一些反映矩阵状况的参数,典型的有以下几种:
(1)能量: 是灰度共生矩阵元素值的平方和,所以也称能量,反映了图像灰度分布均匀程度和纹理粗细度。如果共生矩阵的所有值均相等,则ASM值小;相反,如果其中一些值大而其它值小,则ASM值大。当共生矩阵中元素集中分布时,此时ASM值大。ASM值大表明一种较均一和规则变化的纹理模式。
(2)对比度: ,其中 。反映了图像的清晰度和纹理沟纹深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,CON越大。
(3)相关:它度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。
(4)熵: 是图像所具有的信息量的度量,纹理信息也属于图像的信息,是一个随机性的度量,当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有值几乎相等时,共生矩阵中元素分散分布时,熵较大。它表示了图像中纹理的非均匀程度或复杂程度。
(5)逆差距: 反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
其它参数:
中值<Mean>
协方差<Variance>
同质性/逆差距<Homogeneity>
反差<Contrast>
差异性<Dissimilarity>
熵<Entropy>
二阶距<Angular Second Moment>
自相关<Correlation>
当图像的局部有较小的方差时,则灰度值占有支配地位,当图像的局部有较大的方差时,则纹理占有支配地位。纹理是和局部灰度及其空间组织相联系的,纹理在识别感兴趣的目标和地区中有着非常重要的作用。
灰度共生矩阵表示了灰度的空间依赖性,它表示了在一种纹理模式下的像素灰度的空间关系。它的弱点是没有完全抓住局部灰度的图形特点,因此对于较大的局部,此方法的效果不太理想。灰度共生矩阵为方阵,维数等于图像的灰度级。灰度共生矩阵中的元素(i,j)的值表示了在图像中其中一个像素的灰度值为i,另一个像素的灰度值为j,并且相邻距离为d,方向为A的这样两个像素出现的次数。在实际应用中A一般选择为0°、45°、90°、135°。一般来说灰度图像的灰度级为256,在计算由灰度共生矩阵推导出的纹理特征时,要求图像的灰度级远小于256,主要是因为矩阵维数较大而窗口的尺寸较小则灰度共生矩阵不能很好表示纹理,如要能够很好表示纹理则要求窗口尺寸较大,这样使计算量大大增加,而且当窗口尺寸较大时对于每类的边界区域误识率较大。所以在计算灰度共生矩阵之前需要对图像进行直方图规定化,以减小图像的灰度级,一般规定化后的图像的灰度级为8或16。由灰度共生矩阵能够导出许多纹理特征,本文计算了14种灰度共生矩阵特征,分别为纹理二阶距、纹理熵、纹理对比度、纹理均匀性、纹理相关、逆差分矩、最大概率、纹理方差、共生和均值、共生和方差、共生和熵、共生差均值、共生差方差、共生差熵。
由灰度共生矩阵能够导出许多纹理特征,计算了14种灰度共生矩阵特征,分别为纹理二阶距、纹理熵、纹理对比度、纹理均匀性、纹理相关、逆差分矩、最大概率、纹理方差、共生和均值、共生和方差、共生和熵、共生差均值、共生差方差、共生差熵。
目前,人们对遥感影像上的纹理特征的含义理解不尽相同,纹理有时被称为结构、影纹和纹形等。Pickett认为纹理为保持一定的特征重复性并且间隔规律可以任意安排的空间结构。HawKins认为[6]纹理具有三大标志:某种局部序列性不断重复、非随机排列和纹理区域内大致为均匀的统一体。LiWang和D. C. He认为[7],纹理是纹理基元组成的,纹理基元被认为是表现纹理特征的最小单元,是一个像元在
其周围8个方向上的特征反应。纹理特征有时是明显的,以某种基本图形在某一地区有规律的周期性出现,例如:大面积森林覆盖地区的影像构成的纹理为斑点状,沙漠地区的影像构成的纹理为链状、新月状等;而有时纹理特征是不明显的、隐晦的,具有不稳定性。一般来说,前者纹理比较均一,后者纹理比较复杂[9]。
纹理作为一种区域特征,是对于图像各像元之间空间分布的一种描述。由于纹理能充分利用图像信息,无论从理论上或常识出发它都可以成为描述与识别图像的重要依据,与其他图像特征相比,它能更好地兼顾图像宏观性质与细微结构两个方面,因此纹理成为目标识别需要提取的重要特征。提取纹理特征的方法很多,如基于局部统计特性的特征、基于随机场模型的特征、基于空间频率的特征、分形特征等,其中,应用最广泛的是基于灰值共生矩阵的特征[10]。
%**************************************************************************
% 图像检索——纹理特征
%基于共生矩阵纹理特征提取,d=1,θ=0°,45°,90°,135°共四个矩阵
%所用图像灰度级均为256
%参考《基于颜色空间和纹理特征的图像检索》
%function : T=Texture(Image)
%Image : 输入图像数据
%T : 返回八维纹理特征行向量
%**************************************************************************
% function T = Texture(Image)
Gray = imread('d:result5.bmp');
[M,N,O] = size(Gray);
M = 128;
N = 128;
%--------------------------------------------------------------------------
%1.将各颜色分量转化为灰度
%--------------------------------------------------------------------------
% Gray = double(0.3*Image(:,:,1)+0.59*Image(:,:,2)+0.11*Image(:,:,3));
%--------------------------------------------------------------------------
%2.为了减少计算量,对原始图像灰度级压缩,将Gray量化成16级
%--------------------------------------------------------------------------
for i = 1:M
for j = 1:N
for n = 1:256/16
if (n-1)*16<=Gray(i,j)&Gray(i,j)<=(n-1)*16+15
Gray(i,j) = n-1;
end
end
end
end
%--------------------------------------------------------------------------
%3.计算四个共生矩阵P,取距离为1,角度分别为0,45,90,135
%--------------------------------------------------------------------------
P = zeros(16,16,4);
for m = 1:16
for n = 1:16
for i = 1:M
for j = 1:N
if j<N&Gray(i,j)==m-1&Gray(i,j+1)==n-1
P(m,n,1) = P(m,n,1)+1;
P(n,m,1) = P(m,n,1);
end
if i>1&j<N&Gray(i,j)==m-1&Gray(i-1,j+1)==n-1
P(m,n,2) = P(m,n,2)+1;
P(n,m,2) = P(m,n,2);
end
if i<M&Gray(i,j)==m-1&Gray(i+1,j)==n-1
P(m,n,3) = P(m,n,3)+1;
P(n,m,3) = P(m,n,3);
end
if i<M&j<N&Gray(i,j)==m-1&Gray(i+1,j+1)==n-1
P(m,n,4) = P(m,n,4)+1;
P(n,m,4) = P(m,n,4);
end
end
end
if m==n
P(m,n,:) = P(m,n,:)*2;
end
end
end
%%---------------------------------------------------------
% 对共生矩阵归一化
%%---------------------------------------------------------
for n = 1:4
P(:,:,n) = P(:,:,n)/sum(sum(P(:,:,n)));
end
%--------------------------------------------------------------------------
%4.对共生矩阵计算能量、熵、惯性矩、相关4个纹理参数
%--------------------------------------------------------------------------
H = zeros(1,4);
I = H;
Ux = H; Uy = H;
deltaX= H; deltaY = H;
C =H;
for n = 1:4
E(n) = sum(sum(P(:,:,n).^2)); %%能量
for i = 1:16
for j = 1:16
if P(i,j,n)~=0
H(n) = -P(i,j,n)*log(P(i,j,n))+H(n); %%熵
end
I(n) = (i-j)^2*P(i,j,n)+I(n); %%惯性矩
Ux(n) = i*P(i,j,n)+Ux(n); %相关性中μx
Uy(n) = j*P(i,j,n)+Uy(n); %相关性中μy
end
end
end
for n = 1:4
for i = 1:16
for j = 1:16
deltaX(n) = (i-Ux(n))^2*P(i,j,n)+deltaX(n); %相关性中σx
deltaY(n) = (j-Uy(n))^2*P(i,j,n)+deltaY(n); %相关性中σy
C(n) = i*j*P(i,j,n)+C(n);
end
end
C(n) = (C(n)-Ux(n)*Uy(n))/deltaX(n)/deltaY(n); %相关性
end
%--------------------------------------------------------------------------
%求能量、熵、惯性矩、相关的均值和标准差作为最终8维纹理特征
%--------------------------------------------------------------------------
a1 = mean(E)
b1 = sqrt(cov(E))
a2 = mean(H)
b2 = sqrt(cov(H))
a3 = mean(I)
b3 = sqrt(cov(I))
a4 = mean(C)
b4 = sqrt(cov(C))
sprintf('0,45,90,135方向上的能量依次为: %f, %f, %f, %f',E(1),E(2),E(3),E(4)) % 输出数据;
sprintf('0,45,90,135方向上的熵依次为: %f, %f, %f, %f',H(1),H(2),H(3),H(4)) % 输出数据;
sprintf('0,45,90,135方向上的惯性矩依次为: %f, %f, %f, %f',I(1),I(2),I(3),I(4)) % 输出数据;
sprintf('0,45,90,135方向上的相关性依次为: %f, %f, %f, %f',C(1),C(2),C(3),C(4)) % 输出数据;主要有如下六种:
1.能量,或角度二阶矩(图像均匀性的测度——图像越均匀,其值越大):
![]()
2.熵:

3.最大概率:
![]()
4.对比度(局部图像变化的测度;典型k=2,λ=1):

5.倒数差分矩:

6.相关性(图像线性度的测度,在方向Φ上的线性方向的结构在这个方向上会产生大的相关值):

其中μx,μy 是均值,以及σx,σy是标准差,
![]()


![]()
通用算法如下:
1.给定方向和距离构造共生矩阵。
2.用方向、距离以及六个特征值构成纹理特征向量,这就产生了相关的特征了。
下面是matlab源代码:
main.m
clear all;
close all;
clc;
fai=0;
d=1;
img=imread('lena.jpg');
[m n]=size(img);
k=1;
for i=1:10:m-10 %取10*10的图像,这里我随便写了,准确的是一个挨一个的取10*10
for j=1:10:n-10
re{k}=comatrix(img(i:i+9,j:j+9),fai,d);
k=k+1;
end
end
for j=1:8
s=[]; %存储特征的地方
for i=1:k-1
s=[s re{i}(j)];
end
figure;
plot(s)
end
function re=comatrix(D,fai,d)
[m n]=size(D);
ma=max(D(:));
mi=min(D(:));
D=D-mi+1; %将最小值统一为1
k=ma-mi+1; %产生合适大小的共生矩阵
P=zeros(k,k);
if fai==0
h=0; w=d;
elseif fai==45
h=d; w=d;
elseif fai==90
h=d; w=0;
else
h=d; w=-d;
end
if fai~=135
for i=1:m-h
for j=1:n-w
P(D(i,j),D(i+h,j+w))=P(D(i,j),D(i+h,j+w))+1;
end
end
else
for i=1:m-h
for j=1-w:n
P(D(i,j),D(i+h,j+w))=P(D(i,j),D(i+h,j+w))+1;
end
end
end
if sum(P(:))~=0
P=P/sum(P(:)); %归一化矩阵
end
%re为八个特征值
re=zeros(1,8);
re(1)=fai; %方向特征
re(2)=d; %步长特征
re(3)=sum(P(:).^2); %能量特征
re(4)=max(P(:)); %最大概率特征
miux=sum(double(1:k).*sum(P(1:k,:)));
miuy=sum(double(1:k).*sum(P(:,1:k)));
sigmax=sum((double(1:k)-miux).^2.*sum(P(1:k,:)));
sigmay=sum((double(1:k)-miuy).^2.*sum(P(:,1:k)));
for i=1:k
for j=1:k
if P(i,j)~=0
re(5)=re(5)+P(i,j)*log2(P(i,j)); %熵特征
end
re(6)=re(6)+(i-j).^2*P(i,j); %对比度特征
if i~=j
re(7)=re(7)+P(i,j)/abs(i-j); %倒数差分矩特征
end
re(8)=re(8)+i*j*P(i,j);
end
end
if sigmax*sigmay~=0
re(8)=(re(8)-miux*miuy)/(sigmax*sigmay); %相关性特征
end
end























 4896
4896

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








