62. Unique Paths
Problem
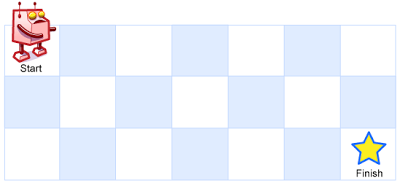
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).
How many possible unique paths are there?
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
问题
一个机器人位于m x n格网的左上角(上图中‘start’标识)。在任何位置,机器人可以向左或者向右走一步。机器人要到达格网的右下角(上图中‘finish’标识)。一共有多少种不同的路径。
提示: m和n不会超过100。
思路1
假设机器人向右走一步即为1,向下走一步记为0,则机器人到达终点时需要向右走n-1步,向下走m-1步。则改题目可以看作n-1个1和m-1个0的组合。因此共有
代码1(C++)
class Solution {
public:
int uniquePaths(int m, int n) {
int M = m+n-2;
int N = m>n ? n-1 : m-1;
long denominator = 1;
long numerator =1;
for (int i =0;i<N;i++){
numerator *= (M-i);
denominator *= (N-i);
}
return numerator/denominator;
}
};注意: 开始没注意m、n不超过100的提醒,计算阶乘时用了int,结果不正确。原因是100的阶乘超过了int的范围,因此计算中要用long。
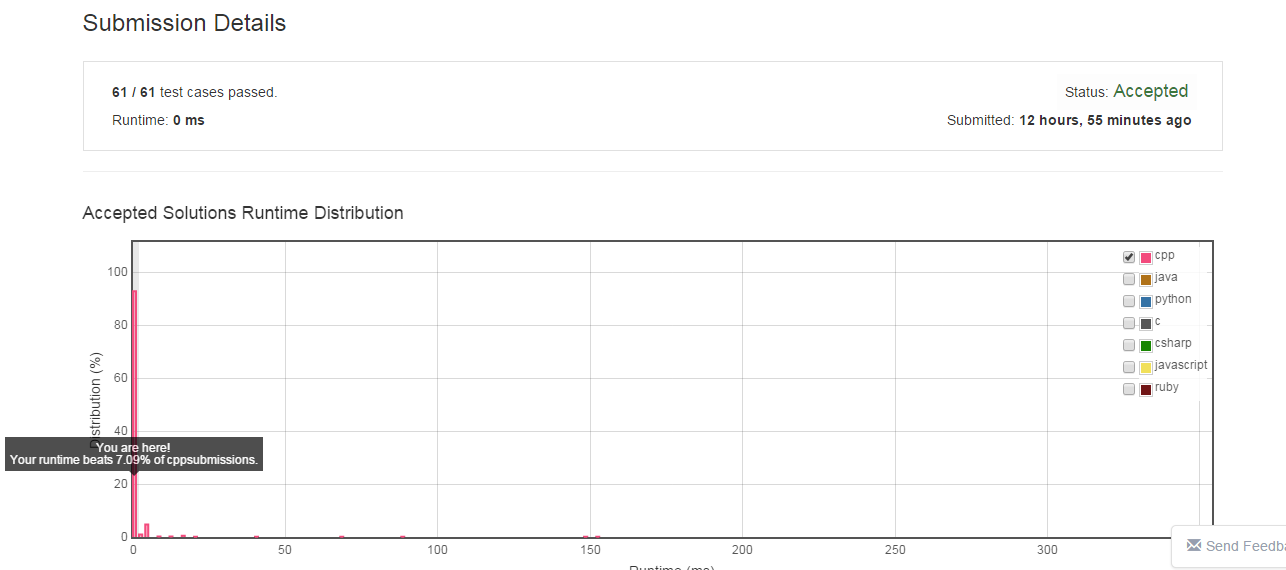
运行结果
思路2
采用动态规划法,到达个格网中任意一个位置的路径总数等于到达这个位置左边网格路径数和上边网格路径数之和,即
代码2(C++)
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> v(m, vector<int>(n, 1));
for(int i=1; i<m; ++i){
for(int j=1; j<n; ++j){
v[i][j]=v[i-1][j]+v[i][j-1];
}
}
return v[m-1][n-1];
}
};







或者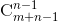
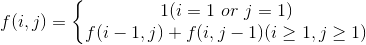














 2782
2782

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








