白化是一种重要的预处理过程,其目的就是降低输入数据的冗余性,使得经过白化处理的输入数据具有如下性质:(i)特征之间相关性较低;(ii)所有特征具有相同的方差。
白化处理分PCA白化和ZCA白化,PCA白化保证数据各维度的方差为1,而ZCA白化保证数据各维度的方差相同。PCA白化可以用于降维也可以去相关性,而ZCA白化主要用于去相关性,且尽量使白化后的数据接近原始输入数据。
1. PCA白化
根据白化的两个要求,我们首先是降低特征之间的相关性。在PCA中,我们选取前K大的特征值的特征向量作为投影方向,如果K的大小为数据的维度n,把这K个特征向量组成选择矩阵U(每一列为一个特征向量),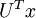
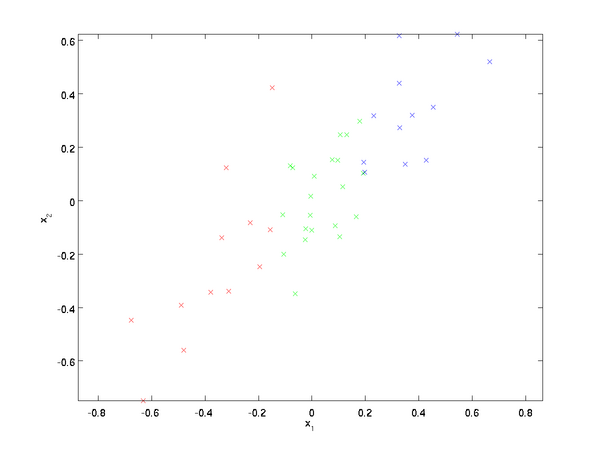
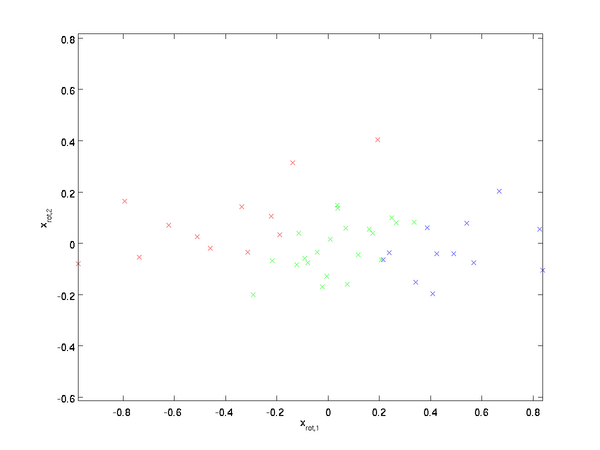
原始数据 PCA旋转
上图显示了原始数据和经过PCA旋转之后的数据,可以发现数据之间的相对位置都没有改变,仅仅改变了数据的基,但这种方法就降低了数据之后的相关性。(原始数据的相关性为正,因为x1增加时,x2也增加;而处理之后的数据的相关性明显降低)
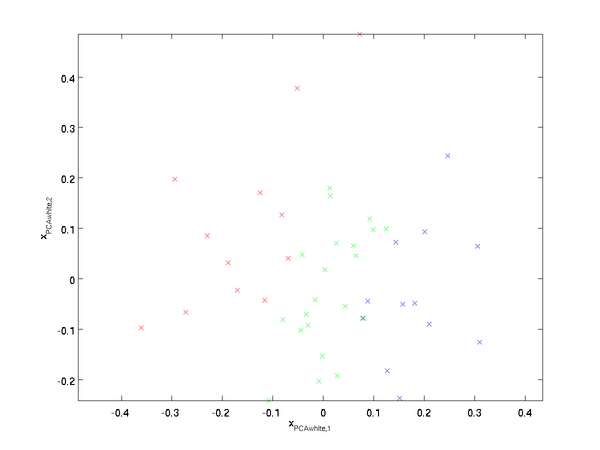
第二个要求是每个输入特征具有单位方差,以直接使用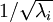
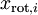
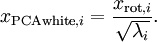
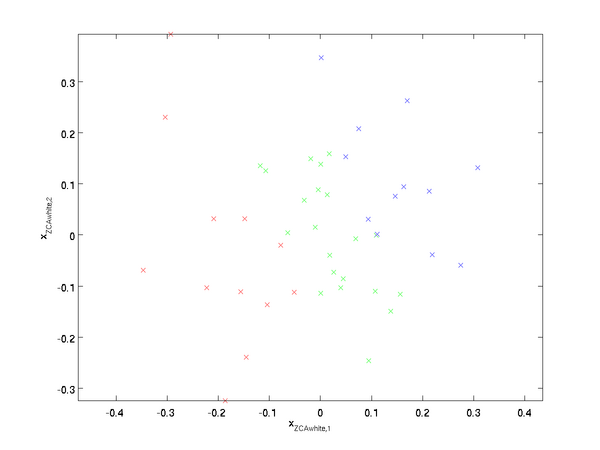
PCA白化 ZCA白化
2. ZCA白化
ZCA白化的定义为:
ZCA白化只是在PCA白化的基础上做了一个旋转操作,使得白化之后的数据更加的接近原始数据。
ZCA白化首先通过PCA去除了各个特征之间的相关性,然后是输入特征具有单位方差,此时得到PCA白化后的处理结果,然后再把数据旋转回去,得到ZCA白化的处理结果,感觉这个过程让数据的特征之间有具有的一定的相关性,下面实验进行验证。
在实验中,我分别计算了原始数据,旋转后数据,PCA白化以及ZCA白化的协方差矩阵,数据用的是UFLDL的实验数据,是个协方差矩阵分别为:
从上面的4个协方差矩阵可以发现,正如上面所述,旋转之后降低了特征之间的相关性,rotate协方差矩阵的主对角线以为的值都接近零。我猜测ZCA白化后的数据的相关性会比PCA白化的要强,在该实验室中表明好像我的感觉是对的,ZCA白化后主对角线以外的值的绝对值大于PCA白化后(今天看了下发现这个有问题),虽然这种比较可以忽略不计,应该他们的值都是非常的接近的。
3. PCA白化和ZCA白化的区别
PCA白化ZCA白化都降低了特征之间相关性较低,同时使得所有特征具有相同的方差。
1. PCA白化需要保证数据各维度的方差为1,ZCA白化只需保证方差相等。
2. PCA白化可进行降维也可以去相关性,而ZCA白化主要用于去相关性另外。
3. ZCA白化相比于PCA白化使得处理后的数据更加的接近原始数据。
4. 正则化
实践中需要实现PCA白化或ZCA白化时,有时一些特征值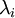
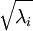
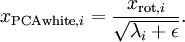
当x在区间 [-1,1] 上时, 一般取值为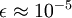








 本文深入探讨了白化处理——一种重要的预处理技术,包括PCA白化和ZCA白化两种方法,对比了它们的特点和应用场景,并介绍了如何在实践中避免数值稳定性问题。
本文深入探讨了白化处理——一种重要的预处理技术,包括PCA白化和ZCA白化两种方法,对比了它们的特点和应用场景,并介绍了如何在实践中避免数值稳定性问题。
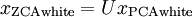


















 1692
1692

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








