在概率论中,对于概率空间 中的事件A1,……,An,当n = 2时容斥原理的公式为:
中的事件A1,……,An,当n = 2时容斥原理的公式为:
当n = 3时,公式为:
一般地:
正数n的唯一素因子分解式=p1^a1 * p2^a2 * p3^a3 ……* pk^ak 。求1,2,3,…… n中与n互素的个数。
-
φ(n)=n(1 - 1/p1) (1 - 1/p2) (1 - 1/p3) (1 - 1/p4)…..(1 - 1/pk) , 其中p1, p2……pk为n的所有质因数
int euler_phi(int n)
{
int m=(int)sqrt(n+0.5);
int ans=n;
for(int i=2;i<=m;i++)
{
if(n%i==0)
{
ans = ans / i * (i-1);
while(n % i == 0)
n/=i;
}
}
if(n>1)
ans = ans / n * (n-1);
return ans;
}








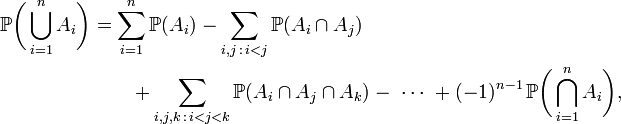














 2134
2134

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








