其他矩阵操作
我们将简单的介绍一些F# PowerPack中提供的关于矩阵的有用的函数与操作符用来总结这部分内容。下面的列表给出了一组相似函数的使用示例。
| 逐点操作
| matrix -> matrix -> matrix 这些函数与操作对作为参数传入的两个矩阵的对应元素执行位操作并将结果作为一个矩阵返回。函数cptMax和cptMin分别返回矩阵中最大与最小的元素, + 执行加操作,.*则执行乘操作。注意:操作*是用在矩阵乘法上。 |
| 逻辑聚合
| (float -> bool) -> matrix -> bool 这些函数实现了对矩阵所有元素的量化操作。函数forall检测是否所有的元素都满足条件,exists则测试是否存在这样的元素满足条件。 |
In-place 操作Matrix.inplaceAddMatrix.inplaceSub | matrix -> matrix -> unit 这些函数执行矩阵的及时加减法,然后将结果存储在第一个矩阵中,并且返回一个unit 的结果。 |
| 全局聚合
| ('a -> float -> 'a) -> 'a -> matrix -> 'a 将矩阵中的所有元素整合到一个单独的值。 这个函数要求一个累计函数,一个初始状态和一个矩阵作为参数。这个累计函数会被矩阵中的每个元素调用。变种函数Matrix.foldi还需将元素的序列表传入此累计函数。 |
| 全局映射
| (float -> float) -> matrix -> matrix 将指定的映射函数应用到输入矩阵的每个元素上,并将得到的结果存储到一个新的矩阵中。变种函数Matrix.mapi还需要将元素的序列表传入次映射函数。 |
使用矩阵乘法的可达性
矩阵乘法在矩阵操作中是一个非常重要的运算操作。在这篇文章中,我不打算解释矩阵相乘的工作机制,但是我会展示如何使用它。
矩阵相乘在处理邻接矩阵是非常有用。邻接矩阵的另一种定义方式就是:所有连接两顶点间的路径长度为1。如果我们将邻接矩阵乘以它自己,我们将得到一些诸如长度为2的路径。下面的代码展示了我们所得到的:
1: m*m
2: val it : Matrix<float> = matrix [ [1.0; 0.0; 0.0; 0.0]
3: [0.0; 2.0; 0.0; 1.0]
4: [0.0; 0.0; 1.0; 1.0]
5: [0.0; 1.0; 1.0; 2.0] ]
右图展示了由矩阵m所表示的图(此图出现在介绍部分)。那么m*m会代表什么呢?表达式m.[1,1]的值表示从顶点1到它自己的路径的条数。数字2.0意味着有两条不同的路径。我们可以从1出发到达2或者3然后返回,这样就可以得到2条不同的路径。另一个有趣的事实就是从顶点2到1(或者其他相似的路线)没有长度为2的路径。他们直接被一条边连接,但是长度为2的路径需要包含多于1条边并且没有添加此边的其它方法。
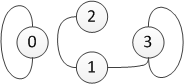
我们可以通过重复使用矩阵相乘来找出哪个顶点与哪个顶点是不可达的。我们将简单的构建一个矩阵,此矩阵中的元素代表长度分别为1,2,….,n的路径的个数,然后查找矩阵中所有为0的元素。为了查找值为0的元素目录,我们可以使用下面的函数:
1: let collectUnreachable paths =
2: paths |> Matrix.foldi (fun i j st value ->
3: if (value <> 0.0) then st else (i, j)::st ) []
4: val collectUnreachable : matrix -> (int * int) list
此函数是使用Matrix.foldi来实现的,此函数迭代此矩阵中的所有元素然后在迭代过程中累计一些状态。我们使用空链表作为初始状态。这个累计函数获取元素的目录,目前累积的目录链表以及当前元素的值.如果它的值为0,那么将当前的目录添加到链表中,否则我们只返回它的原始状态。
下面的代码清单使用此函数来查找那些路径长度为1的不可到达的顶点,以及任意某路径长度的不可达顶点(四个顶点的图中,不重复任意一条边的情况下,其最长可能路径伟3,因此我们只需检测这个长度的路径即可):
1: collectUnreachable m
2: val it : (int * int) list =
3: [ (3, 2); (3, 0); (2, 3); (2, 2); (2, 0);
4: (1, 1); (1, 0); (0, 3); (0, 2); (0, 1) ]
5:
6: let paths = m + m * m + m * m * m
7: val paths : matrix = matrix [ ... ]
8:
9: collectUnreachable paths
10: val it : (int * int) list = [ (3, 0); (2, 0); (1, 0); (0, 3); (0, 2); (0, 1) ]
在第一种情况中,我们调用这个函数并将原矩阵作为参数传入,然后我们得到那些没有边直接相连的顶点对。注意,我们没有做任何的操作来去除对称的顶点,因此这里的结果中包含了如(2,3)和(3,2)这样的顶点对。接下来,我们通过将原邻接矩阵加上m乘以m再加上 m乘以m在乘以m得到矩阵的路径。这会得到结果为长度为1,2和3的目录矩阵。如果我们在此矩阵中找不可到达的顶点时,我们会发现无法找到从顶点0到任何其他顶点可达的路径,除此外其他的顶点都是相连接的。这就是我们看过此图后所期待的结果。
普通矩阵的简介
到目前为止,我们接触的矩阵存储的元素均为float类型。这是矩阵中最常用的类型并且你可能在F#中的大部分时间都会碰到它。为了涵盖最常见的情况,F#提供了matrix类型。然而,有时我们也可能碰到需要创建矩元素类型为int,decimal或者其他用户自定义的提供一些数据操作的数字类型的矩阵,这也是可能的。
在下面的两段代码清单上,我们将看看一个简单示例,示例中我们使用普通矩阵重新实现了本文早些时候讨论的一些功能。我们将使用int类型取代float来表示两个顶点间的路径数量。首先,我们需要创建一个普通矩阵。这可以通过使用Matrix.Generic模块中的函数实现。为了使此模块更容易被访问,我们可以先定义一个模块的别名:
1: module MatrixG = Matrix.Generic
函数matrix仅工作在浮点数据上。幸运的是,我们可以使用函数MatrixG.ofSeq来做相同的事,但是它对任意类型都有效。这样一来,我们就可以使用我们此前见过的,熟悉的矩阵操作:
1: let m = Matrix.Generic.ofSeq [ [ 0; 0; 1 ]
2: [ 0; 1; 0 ]
3: [ 1; 0; 1 ] ]
4: val m : Matrix<int> = matrix [ ... ]
5:
6: let paths = m + m * m
7: val it : Matrix<int> = matrix [ [1; 0; 2
8: [0; 2; 0
9: [2; 0; 3] ]
上面的代码首先创建一个包含整数的矩阵,然后使用矩阵间的逐点除和矩阵乘法来获取代表两点间距离长度为1或者2的矩阵。创建一个元素类型为非数字类型的矩阵如字符串,这样的做法是没什么价值的。确实,这样做是可以的,但是这种情况下,一些操作如+和* 就会抛出异常,因为字符串类型并不支持它们。不过,一些其他操作如map或则fold这对任意类型的矩阵均可用。
模块Matrix中的大部分函数对于Matrix.Generic模块来说同样可用。最后一个示例展示了如何在整数型的邻接矩阵中查找不可达顶点的组合:
1: paths |> MatrixG.foldi (fun i j st value ->
2: if (value = 0) then (i, j)::st else st) []
3: val it : (int * int) list = [(2, 1); (1, 2); (1, 0); (0, 1)]
上面的代码同早些时候我们使用MatrixG模块中的函数foldi时的代码是一样的。如果我们看看运行结果,我们可以看到在矩阵中没有讲顶点1和其他顶点相连的边。
总结
这篇文章描述了如何使用F#PowerPack中的matrix类型来实现利用邻接矩阵完成图的一些算法。我们看过了用来创建矩阵的函数,使用切割法访问矩阵元素,以及一些F# PowerPack提供的与矩阵相关的一些操作。
matrix类型支持了大部分我们需要的标准操作(例如矩阵乘法),但是这些操作的实现并没有得到很好的优化。这意味着或许用它来表示图或者解决其他不需要大量计算的问题是一种好的选择。然而,此类型并不适用于需要高效的数字计算。
如果你对性能感兴趣,那么你可以看看F# MathProvider,它提供了对matrix类型中的一些操作的高效实现——使用Blas和Lapack进行包装。或者,这里也有大量适用于F#的数字语言库,其中很重要的一个开源项目就是Math.NET Numerics。引用与链接
- F# PowerPack(原代码与二进制包)- CodePlex
- 数字计算–MSDN上的现实中的函数式编程
- F#与.NET的数字语言库 - MSDN上的现实中的函数式编程
- F# MathProvider– CodePlex
- Math.NET Numerics - .NET开源数学








 本文介绍了F#PowerPack中的矩阵操作与图算法,包括矩阵的逐点操作、逻辑聚合、in-place操作、全局聚合与映射,以及如何利用矩阵乘法实现图的可达性分析。还展示了如何在整数型邻接矩阵中查找不可达顶点的组合。
本文介绍了F#PowerPack中的矩阵操作与图算法,包括矩阵的逐点操作、逻辑聚合、in-place操作、全局聚合与映射,以及如何利用矩阵乘法实现图的可达性分析。还展示了如何在整数型邻接矩阵中查找不可达顶点的组合。
















 11
11

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








