UVa 1440 - Inspection

仅有下界的最小流
介于很多小伙伴都是第一次做这种类型的题目 ， 我就详细讲讲思路吧.

让我们先看看这个算法的大致轮廓
1. 添加超级源点、汇点 ， 并找到一个可行流（满足下界的流量图）
2. 返回尽量多的流 ， 并且保持 满足下界 这个条件
3. 输出一组方案

• 怎么找到一个可行流呢？ 可以按照白书上面的思路 ， 重置路径 ， 然后求一组可行解 。 但基于这个问题的特殊性（$DAG$） ，我们可以构造一个刚好满足下界的可行流。

• 对于每个点 ， 计算入度和出度。 对于每一个点 ， 如果出度>入度 ， 那么我们从超级源点S向这个点连一条边 ， 流量为这个点的出度－入度。这相当于把这个点当作起点 ， 开始一些新的航行。 相似的 ， 如果入度>出度 ， 那么我们从这个点向超级汇点连一条边 ， 流量为入度－出度。

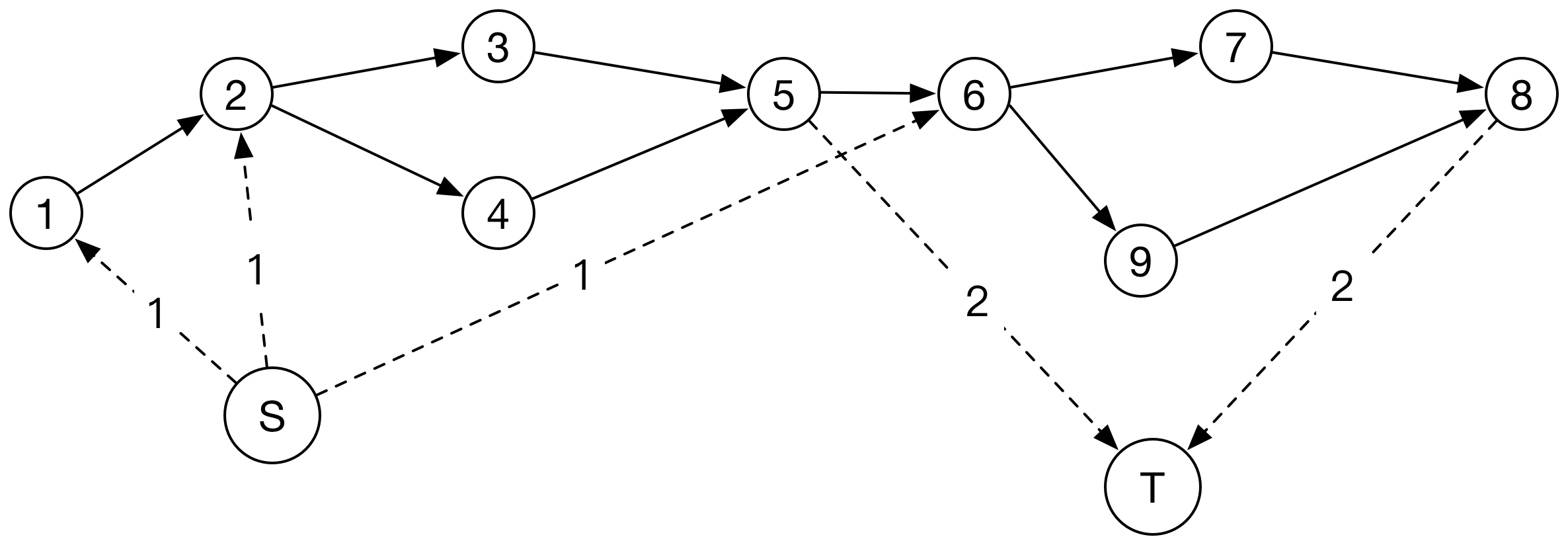
• 图示如下：

加上S和T ， 并增加新边后：

注意 ， 5->T的边上的流量应该为1 ， 误写成2.

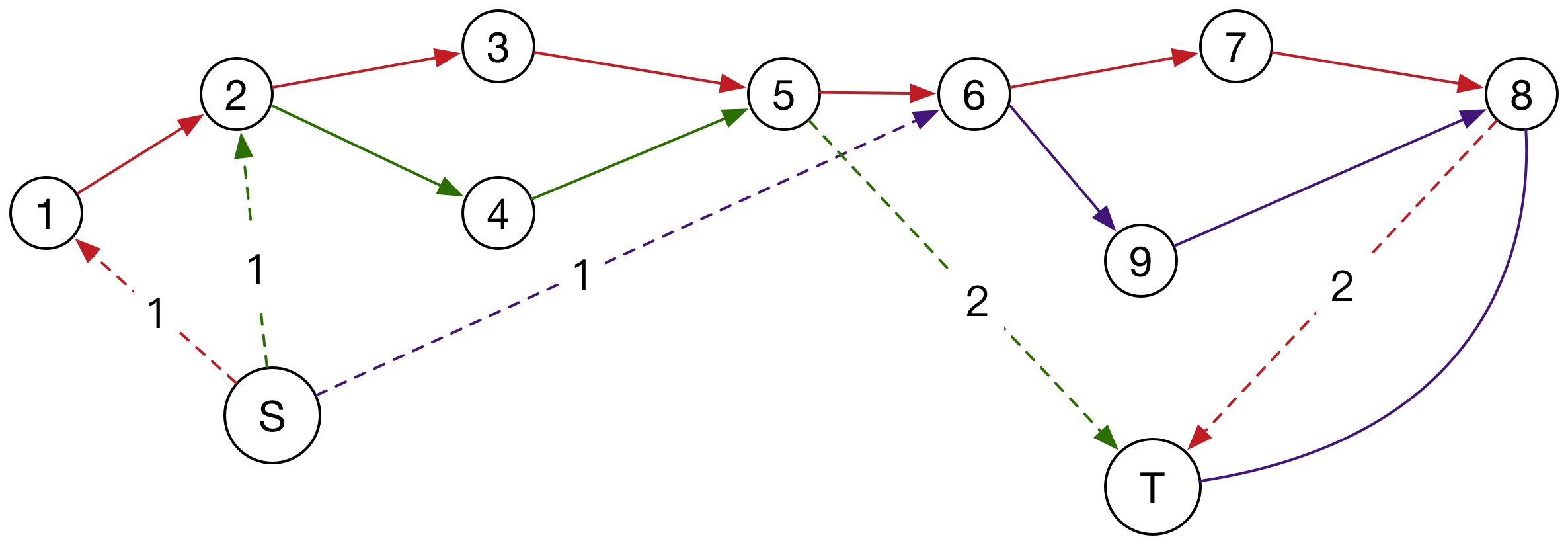
这里流量3对应的路径图：

每个图都是可以这样找到一个可行的流量图的。

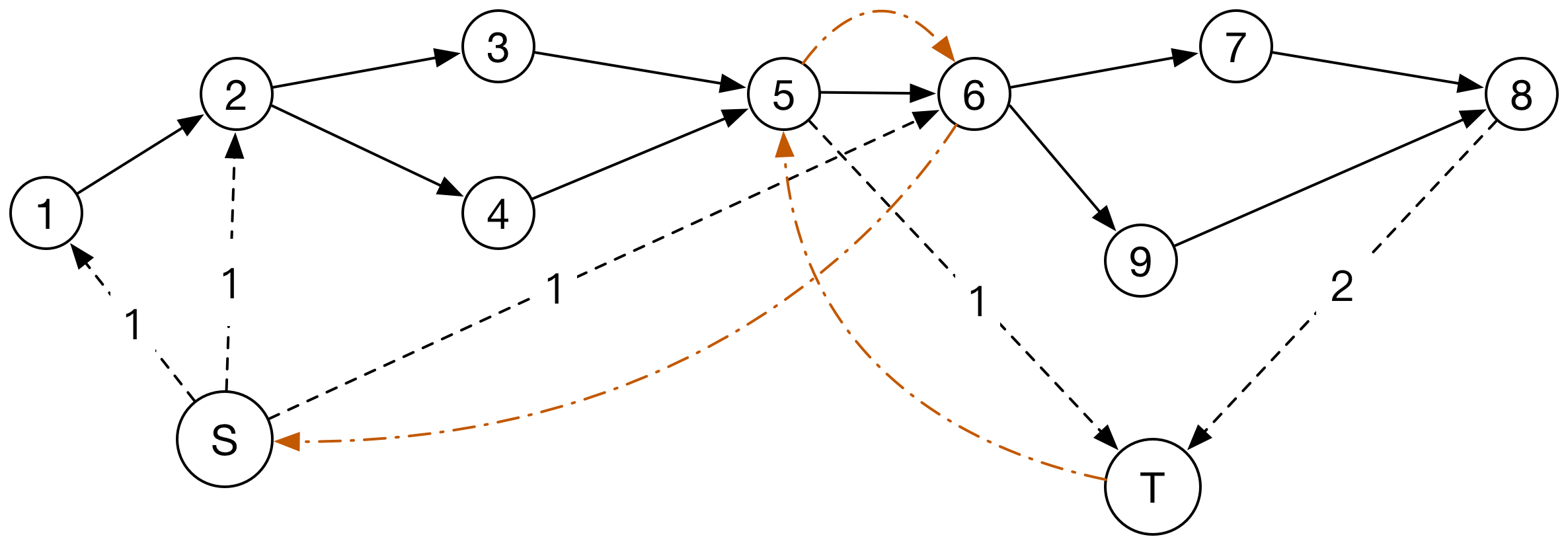
• 那么 ， 怎么返回尽量多的流量呢？ 首先让我们看看这个图怎么返回流量的:

• 显然 ， 这个图只需要两次航行就可以了 ， 但这里的流量为3 ， 所以有一个流量需要从T经过反向边 ， 回到S。 如图 ， $T -> 5 -> 6 -> S$就是这样的一条路径。

• 其实在修改后的图中 ， 另一个航行是沿着：
  $S -> 2 -> 4 -> 5 -> 6 -> 9 -> 8 -> T$

• 这就启发我们 ， 在不违反下界的前提下 ， 找一个从$T$到$S$的最大流就OK了。
  UP： 那如何不违反下界呢 ， 其实我们在建图的时候耍一点小把戏 ， 把有下界的边的反向边容量设为0就可以啦！

关于最后找路径 ， 其实并不麻烦 ， 从 S <script type="math/tex" id="MathJax-Element-18">S</script>开始沿着增广路找就可以了。
整个程序需要注意一些细节的处理。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <string>
#include <vector>
#include <deque>
#include <stack>
#include <algorithm>
#include <queue>

using namespace std;
const int maxn = 150;
const int INF = 0x3f3f3f3f;
struct edge { int t , c , re , v; edge(int t = 0 , int c =0  , int re = 0 , int v = 0):t(t),c(c),re(re),v(v){} };


int n;
vector<edge> g[maxn];
int d[maxn];

void addEdge(int a , int b , int c , int modi = 0)
{
    g[a].push_back(edge(b , c , g[b].size() , 1));
    g[b].push_back(edge(a , 0 , g[a].size() - 1));

    if(modi)
    {
        g[a].back().c-=modi;
        g[b].back().c+=modi;
    }
}


int level[maxn];
int iter[maxn];

bool bfs(int s , int t)
{
    memset(level, INF, sizeof(level));
    queue<int> q;
    q.push(s);  
    level[s] = 0;

    while(!q.empty())
    {
        int now = q.front();
        q.pop();

        for(int i=0;i<g[now].size();i++)
        {
            edge& e = g[now][i];
            if(level[e.t]==INF && e.c>0)
            {
                level[e.t] = level[now]+1;
                q.push(e.t);
            }
        }
    }
    return level[t]!=INF;
}

int dfs(int s , int t , int flow)
{
    if(s==t || !flow) return flow;

    for(int& i = iter[s];i<g[s].size();i++)
    {
        edge& e = g[s][i];
        if(level[e.t]!=level[s]+1) continue;

        int f = dfs(e.t, t, min(flow, e.c));
        if(f>0)
        {
            e.c-=f;
            g[e.t][e.re].c+=f;
            return f;
        }
    }
    return 0;
}

int MaxFlow(int s , int t)
{
    int res = 0;
    while(bfs(s, t))
    {
        memset(iter, 0, sizeof(iter));
        int flow;
        while((flow = dfs(s, t, INF))>0) res+= flow;
    }
    return res; 
}

bool extend(int u , int s , int t)
{
    if(u==t) return true;
    for(int i=0;i<g[u].size();i++)
    {
        edge& e = g[u][i];
        if(!g[e.t][e.re].c || !e.v) continue;
        g[e.t][e.re].c--;
        if(e.t!=t) cout<<(u==s?"":" ")<<e.t;
        return extend(e.t, s, t);
    }
    return false; 
}

int main(int argc, char *argv[]) {

    while(cin>>n && n)
    {
        memset(d, 0, sizeof(d));
        for(int i=0;i<=n+1;i++) g[i].clear();

        for(int i=1;i<=n;i++)
        {
            int num;
            cin>>num;

            while(num--)
            {
                int x;
                cin>>x;
                d[x]++;
                d[i]--;
                addEdge(i, x, INF);
            }
        }
        int S = 0 , T = n+1 , flow = 0;
        for(int i=1;i<=n;i++) 
            if(d[i]>0)
                addEdge(i, T, INF , d[i]) , flow+=d[i];
            else if(d[i]<0)
                addEdge(S, i, INF ,-d[i]);

        flow-= MaxFlow(T, S);

        for(int i=1;i<=n;i++) for(int j=0;j<g[i].size();j++) if(g[i][j].v && g[i][j].t!=S && g[i][j].t!=T)
        {
            edge& e = g[i][j];
            g[e.t][e.re].c++;
        }

        cout<<flow<<endl;
        while(extend(S, S, T)) cout<<endl; 

    }

    return 0;
}