题解参考:http://blog.sina.com.cn/s/blog_86942b140101450q.html
Description
给定一张有向图,每条边都有一个容量C和一个扩容费用W。这里扩容费用是指将容量扩大1所需的费用。
求:
1、 在不扩容的情况下,1到N的最大流;
2、 将1到N的最大流增加K所需的最小扩容费用。
Input
输入文件的第一行包含三个整数N,M,K,表示有向图的点数、边数以及所需要增加的流量。 接下来的M行每行包含四个整数u,v,C,W,表示一条从u到v,容量为C,扩容费用为W的边。
Output
输出文件一行包含两个整数,分别表示问题1和问题2的答案。
Sample Input
5 8 2
1 2 5 8
2 5 9 9
5 1 6 2
5 1 1 8
1 2 8 7
2 5 4 9
1 2 1 1
1 4 2 1
1 2 5 8
2 5 9 9
5 1 6 2
5 1 1 8
1 2 8 7
2 5 4 9
1 2 1 1
1 4 2 1
Sample Output
13 19
30%的数据中,N<=100
100%的数据中,N<=1000,M<=5000,K<=10
【分析】
第一问很显然,直接SAP跑一遍最大流即可。
第二问的话,明显是费用流。但是有两个问题,
- 第一次最大流跑出来的残量图对于最小费用来说不一定最优,可能需要退流。
- 还可以扩容。
我们可以想到,答案可能在多条路上扩容。我们的目的是尽量经过那些还有残余流量与扩容费用较小的边。
而残量图不一定最优,简单的求费用流肯定不行。
那么我们可不可以重新建图,使如此复杂的问题变为求简单的费用流的问题呢?
在第一次的基础上,将残量图的原来所有边价值清零,残量不变,表示在该残量上扩容不需要代价。
新建所有边的附属边,价值为原来的价值,残量为max(K-flow,0),表示在原来流量flow上扩容至K,每加1流的代价为W。限制总流量为K。
然后跑一次费用流即可。
原图:

残余网络:
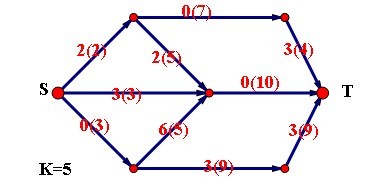
建边:
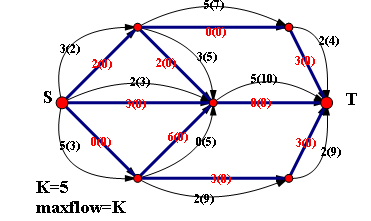
【代码】
/* ID:Ciocio LANG:C++ DATE:2013-12-05 TASK:Network */ #include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <iostream> #include <algorithm> #include <queue> using namespace std; #define MAXM 40000 #define MAXN 1005 #define INF 999999999 int N,M,K,Sta,End,Maxflow,Mincost; int X[MAXM],Y[MAXM],Last[MAXM],Next[MAXM],C[MAXM],W[MAXM]; int G[MAXN][MAXN],dis[MAXN],vd[MAXN],path[MAXN],edge[MAXN]; bool vis[MAXN]; int tot=1; void _addedge(int a,int b,int c,int w) { tot++; X[tot]=a; Y[tot]=b;C[tot]=c;W[tot]=w; Next[tot]=Last[a]; Last[a]=tot; tot++; Y[tot]=a;C[tot]=0;W[tot]=-w; Next[tot]=Last[b]; Last[b]=tot; } void _init() { scanf("%d%d%d",&N,&M,&K); int u,v,c,w; for(int i=1;i<=M;i++) { scanf("%d%d%d%d",&u,&v,&c,&w); G[u][v]=w; _addedge(u,v,c,0); } Sta=1;End=N; } int _SAP(int u,int flow) { if(u==N) return flow; int delta=0; for(int j=Last[u];j;j=Next[j]) { int v=Y[j]; if(C[j]>0&&dis[u]==dis[v]+1) { int temp=_SAP(v,min(flow-delta,C[j])); C[j]-=temp; C[j^1]+=temp; delta+=temp; if(delta==flow) return delta; } } if(dis[Sta]>=N) return delta; vd[dis[u]]--; if(vd[dis[u]]==0) dis[Sta]=N; dis[u]++; vd[dis[u]]++; return delta; } queue <int> Q; bool _findpath() { for(int i=Sta;i<=End;i++) {dis[i]=INF;path[i]=-1;vis[i]=false;edge[i]=0;} dis[Sta]=path[Sta]=0;vis[Sta]=true; while(!Q.empty()) Q.pop(); Q.push(Sta); while(!Q.empty()) { int u=Q.front();Q.pop(); vis[u]=false; for(int j=Last[u];j;j=Next[j]) { int v=Y[j]; if(C[j]>0&&dis[v]>dis[u]+W[j]) { dis[v]=dis[u]+W[j]; path[v]=u;edge[v]=j; if(!vis[v]) { vis[v]=true; Q.push(v); } } } } return dis[End]<INF; } void _addflow() { int flow=INF,cost=0,i; i=End; while(i!=Sta&&path[i]!=0&&edge[i]!=0) { flow=min(flow,C[edge[i]]); cost+=W[edge[i]]; i=path[i]; } Maxflow+=flow; Mincost+=flow*cost; i=End; while(i!=Sta&&path[i]!=0&&edge[i]!=0) { C[edge[i]]-=flow; C[edge[i]^1]+=flow; i=path[i]; } } void _solve() { int ans=0; while(dis[Sta]<End) ans+=_SAP(Sta,INF); cout<<ans<<" "; M=tot; for(int i=2;i<=M;i+=2) { int u=X[i],v=Y[i]; _addedge(u,v,max(K-C[i],0),G[u][v]); } Maxflow=Mincost=0; while(_findpath()) { _addflow(); if(Maxflow>=K) break; } cout<<Mincost<<endl; } int main() { _init(); _solve(); return 0; }





 本文介绍了解决特定有向图问题的方法:在不扩容条件下求得源点到汇点的最大流,并计算增加额外流量所需的最小扩容费用。通过两阶段算法实现:首先使用SAP算法找出最大流,随后构建新的边集并运用费用流算法确定最优扩容方案。
本文介绍了解决特定有向图问题的方法:在不扩容条件下求得源点到汇点的最大流,并计算增加额外流量所需的最小扩容费用。通过两阶段算法实现:首先使用SAP算法找出最大流,随后构建新的边集并运用费用流算法确定最优扩容方案。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








