46 - Permutations（全排列和递归）

hellochenlu

于 2016-03-03 10:37:44 发布

阅读量1.3k

点赞数 2

CC 4.0 BY-SA版权

分类专栏： LeetCode leetcode解法大全

本文链接：https://blog.csdn.net/hellochenlu/article/details/50785822

LeetCode 同时被 2 个专栏收录

41 篇文章

订阅专栏

leetcode解法大全

5 篇文章

订阅专栏

本文介绍了一种生成所有可能的全排列的方法。通过递归交换元素位置实现，将大问题拆解为小问题来求解。具体步骤包括：1) 交换首个元素与其他所有元素；2) 固定首个元素后进入下一层递归；3) 直至最后一个元素固定并输出结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Given a collection of distinct numbers, return all possible permutations.

For example,
[1,2,3] have the following permutations:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1].
Subscribe to see which companies asked this question

思路：

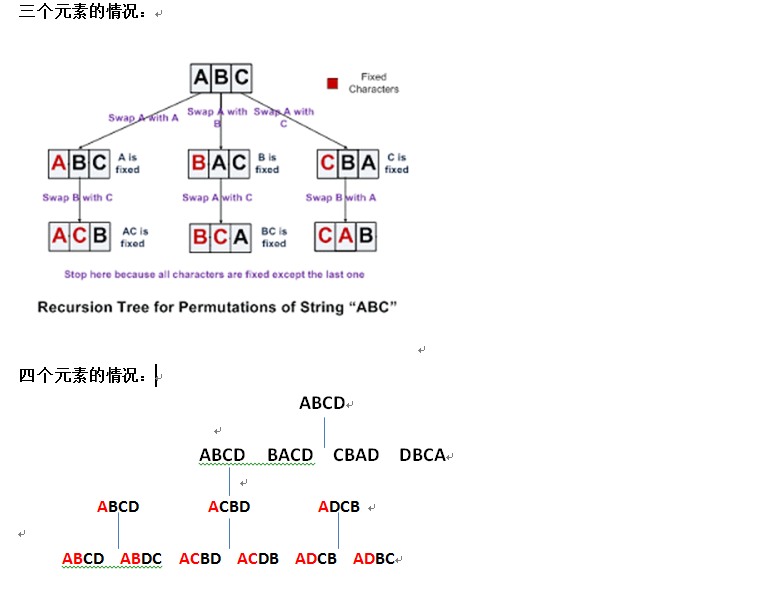
一、全排列

where for the length of n, the permutations can be generated by
(1) Swap the 1st element with all the elements, including itself.
(2) Then the 1st element is fixed, go to the next element.
(3) Until the last element is fixed. Output.
It's more clear in the figure above. The key point is to make the big problem into smaller problem, here is how to convert the length n permutation into length n-1 permutation problem.

代码：

class Solution {
public:
     
    void perm(vector<int> num,int k,int n, vector<vector<int> > &res){
        if (k==n){
            res.push_back(num);
        }else{
            for (int i=k;i<=n;i++){
                int tmp = num[k];
                num[k]=num[i];
                num[i]=tmp;
                 
                perm(num,k+1,n,res);
                 
                tmp = num[k];
                num[k]=num[i];
                num[i]=tmp;
            }
        }
    }
 
    vector<vector<int> > permute(vector<int> &num) {
        // Start typing your C/C++ solution below
        // DO NOT write int main() function
        vector<vector<int> > res;
        perm(num,0,(num.size()-1),res);
        return res;
    }
};