活动选择问题是《算法导论》里面关于贪心算法的第一个问题。这个问题是这样的。我们有一组活动,每个活动都有一个开始时间Si和结束时间Fi。如下图:
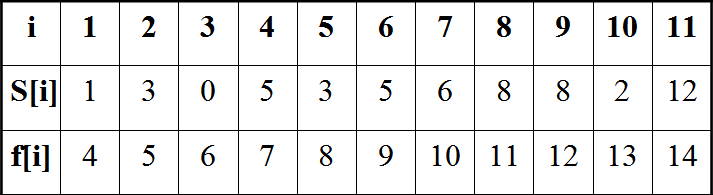
每个活动都共享同一个公共的资源(比如教室等)所以同一时间只能有一个活动。现在的问题就是要在指定的时间内让举办的活动数量做大。
这个问题是贪心算法一个典型的应用。说到贪心,贪心基本解决问题的方案就是
#1.尽可能在局部找到一个最优的解
#2然后证明这个局部的优化解是全局优化解的一部分
#3最后把这个局部解用递归或者迭代的方式推广到全局。
所谓贪心,一般都会把带选择的资源做个权重的排序,每次的最优化子结构的选取其实就是最大权重的选取。就这个活动选择问题而言,我们将所有的活动结束时间排序。这里的局部最优解就是指到特定的时间Fi为止的最优解。这个最优解的贪心意义体现在每次最优解利用了最早结束时间,从而是剩余时间最大化。








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1331
1331

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








