传送门:http://www.wikioi.com/problem/3123/
FFT,快速傅里叶变换,蒟蒻看别人的题解都太深奥,看不懂,好不容易学会,以蒟蒻的理解写给那些想学FFT却又找不到合适的资料的OIer,蒟蒻理解有限,难免有许多错误,请大家多多包涵。
快速傅里叶变换
百度的各种讲解都TM扯什么频率什么的,蒟蒻完全看不懂,后来认真看了看算导,获益匪浅,算导上讲的真心不赖,有很多内容都来自算导。
1.多项式
多项式的两种表达方式:系数表达和点值表达
系数表达就是大家常用的表达方式,点值表达就像在这个多项式函数上取n个不同的点,这样就可以确定原多项式。
比如说二次函数需要3个点就可以确定,一次函数需要2个点,一个n次多项式需要n个点(n次多项式意思是有0..n-1次幂的多项式)
A(x)=x^2+2*x-1可以被表达为{ ( 0 , -1 ) , ( 1 , 2 ) , ( 2 , 7 ) }
加法和乘法:
B(x)=x^2-x+2 { ( 0 , 2 ) , ( 1 , 2 ) , ( 2 , 4 ) }
C(x)=A(x)+B(x)=2x^2+x+1 { ( 0, 1) , ( 1 , 4 ) , ( 2, 11 ) }
注意乘法需要2n个点 lz比较懒就不写了……
于是我们得到一个计算多项式的方法:
2.n次单位复数根
有关复数根的性质可以百度到,不再赘述
http://baike.baidu.com/link?url=017EPfseoBwVxWpWPm5aunUn8x9dmRvioav9IubYLSKEGngK8_rDV2bd4PFCM8sJ
3.DFT&&FFT
使用单位根计算点值表达式叫DFT(离散傅里叶变换)复杂度n^2,FFT是其优化版复杂度nlogn
计算FFT的伪代码(好吧用的是python的高亮)
下划线代表的是下标,括号代表上标,for 循环的range是左闭右开的
FFT(a):
n=a.length()
if n==1:
return a
w_n=e^(pi*i/n)=complex(cos(2*pi/n),sin(2*pi/n))
w=1
a(0)=[a0,a2,...a_n-2]
a(1)=[a1,a3,...a_n-1]
y(0)=FFT(a(0))
y(1)=FFT(a(1))
for k in range(0,n/2):
y_k=y_k(0)+w*y_k(1)
y_k+n/2=y_k(0)-w*y_k(1)
w=w*w_n
return y4.递归=>迭代??
FFT的for循环中有两次w_n^k*y_k(1)的计算,于是可以改写成这样
for k in range(0,n/2):
t=w*y_k(1)
y_k=y_k(0)+t
y_k+n/2=y_k(0)-t
w=w*w_n
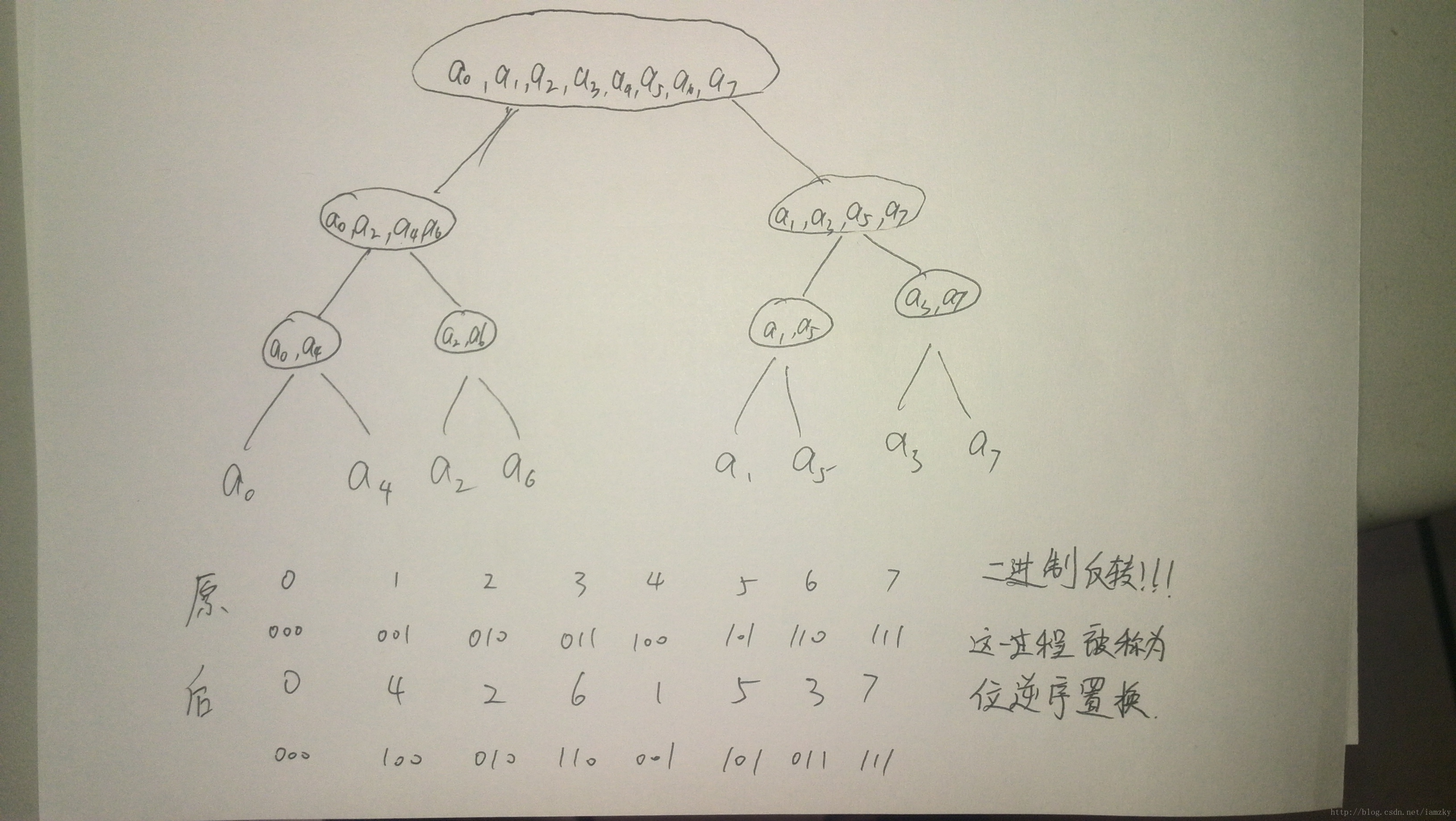
#这一过程被称蝴蝶操作观察每次按照奇偶位置分割所形成的树:
每个数和他二进制相反的位置互换!!
伪代码(算导给的真是……)
BIT-REVERSE-COPY(a,A):
n=a.length()
for k in range(0,n):
A[rev(k)]=a_k
#算导说rev函数很好写,就没写……于是我们给出FFT的迭代实现的伪代码:
FFT(a):
BIT-REVERSE-COPY(a,A)
n=a.length()
for s in range(1,log2(n)+1):
m=2^s
w_m=e^(2*pi*i/m)=complex(cos(2*pi*m),sin(2*pi*m))
for k in range(0,n,m):
w=1
for j in range(0,m/2):
t=w*A[k+j+m/2]
u=A[k+j]
A[k+j]=u+t
A[k+j+m/2]=u-t
w=w*w_m
return A#include<bitset>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define N 400005
#define pi acos(-1.0) // PI值
using namespace std;
struct complex
{
double r,i;
complex(double real=0.0,double image=0.0){
r=real; i=image;
}
// 以下为三种虚数运算的定义
complex operator + (const complex o){
return complex(r+o.r,i+o.i);
}
complex operator - (const complex o){
return complex(r-o.r,i-o.i);
}
complex operator * (const complex o){
return complex(r*o.r-i*o.i,r*o.i+i*o.r);
}
}x1[N],x2[N];
char a[N/2],b[N/2];
int sum[N]; // 结果存在sum里
int vis[N];
void brc(complex *a,int l){//原来神犇的二进制平摊反转置换太神看不懂,蒟蒻写了一个O(n)的……
memset(vis,0,sizeof(vis));//O(logn)的在后面
for(int i=1;i<l-1;i++){
int x=i,y=0;
int m=(int)log2(l)+0.1;
if(vis[x])continue;
while(m--){
y<<=1;
y|=(x&1);
x>>=1;
}
vis[i]=vis[y]=1;
swap(a[i],a[y]);
}
}
void fft(complex *y,int l,double on) // FFT O(nlogn)
// 其中on==1时为DFT,on==-1为IDFT
{
register int h,i,j,k;
complex u,t;
brc(y,l); // 调用反转置换
for(h=2;h<=l;h<<=1) // 控制层数
{
// 初始化单位复根
complex wn(cos(on*2*pi/h),sin(on*2*pi/h));
for(j=0;j<l;j+=h) // 控制起始下标
{
complex w(1,0); // 初始化螺旋因子
for(k=j;k<j+h/2;k++) // 配对
{
u=y[k];
t=w*y[k+h/2];
y[k]=u+t;
y[k+h/2]=u-t;
w=w*wn; // 更新螺旋因子
} // 据说上面的操作叫蝴蝶操作…
}
}
if(on==-1) for(i=0;i<l;i++) y[i].r/=l; // IDFT
}
/*
void fft2(complex *a,int s,int t){//蒟蒻自己写的递归版FFT,不保证正确 ,代码内部有未定义变量
if((n>>t)==1)return;//s记录起始,t记录深度,调用时应从0开始
fft(a,s,t+1);
fft(a,s+(1<<t),t+1);
for(int i=0;i<(n>>(t+1));i++){
p=(i<<(t+1))+s;
wt=w[i<<t]*a[p+(1<<t)];
tt[i]=a[p]+wt;
tt[i+(n>>(t+1))]=a[p]-wt;
}
for(i=0;i<(n>>t);i++)a[(i<<t)+s]=tt[i];
}*/
int main(void)
{
int l1,l2,l;
register int i;
while(scanf("%s%s",a,b)!=EOF)
{
l1=strlen(a);
l2=strlen(b);
l=1;
while(l<l1*2 || l<l2*2) l<<=1; // 将次数界变成2^n
// 配合二分与反转置换
for(i=0;i<l1;i++) // 倒置存入
{
x1[i].r=a[l1-i-1]-'0';
x1[i].i=0.0;
}
for(;i<l;i++) x1[i].r=x1[i].i=0.0;
// 将多余次数界初始化为0
for(i=0;i<l2;i++)
{
x2[i].r=b[l2-i-1]-'0';
x2[i].i=0.0;
}
for(;i<l;i++) x2[i].r=x2[i].i=0.0;
fft(x1,l,1); // DFT(a)
fft(x2,l,1); // DFT(b)
for(i=0;i<l;i++) x1[i]=x1[i]*x2[i]; // 点乘结果存入a
fft(x1,l,-1); // IDFT(a*b)
for(i=0;i<l;i++) sum[i]=x1[i].r+0.5; // 四舍五入
for(i=0;i<l;i++) // 进位
{
sum[i+1]+=sum[i]/10;
sum[i]%=10;
}
l=l1+l2-1;
while(sum[l]<=0 && l>0) l--; // 检索最高位
for(i=l;i>=0;i--) putchar(sum[i]+'0'); // 倒序输出
putchar('\n');
}
return 0;
}
/*void brc(complex *y,int l) // 二进制平摊反转置换 O(logn)
{
register int i,j,k;
for(i=1,j=l/2;i<l-1;i++)
{
if(i<j) swap(y[i],y[j]); // 交换互为下标反转的元素
// i<j保证只交换一次
k=l/2;
while(j>=k) // 由最高位检索,遇1变0,遇0变1,跳出
{
j-=k;
k>>=1;
}
if(j<k) j+=k;
}
}*/pyc神犇的写法,bzoj3527,zjoi2014 力,无限YM
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1000010;
int n,N,L;
int rev[maxn];
int dig[maxn];
double p[maxn];
struct cp{
double r,i;
cp(double _r=0,double _i=0):
r(_r),i(_i){}
cp operator+(cp x){return cp(r+x.r,i+x.i);}
cp operator-(cp x){return cp(r-x.r,i-x.i);}
cp operator*(cp x){return cp(r*x.r-i*x.i,r*x.i+i*x.r);}
};
cp a[maxn],b[maxn],c[maxn],A[maxn],x,y;
void FFT(cp a[],int flag){
for(int i=0;i<N;i++)A[i]=a[rev[i]];
for(int i=0;i<N;i++)a[i]=A[i];
for(int i=2;i<=N;i<<=1){
cp wn(cos(2*M_PI/i),flag*sin(2*M_PI/i));
for(int k=0;k<N;k+=i){
cp w(1,0);
for(int j=0;j<i/2;j++){
x=a[k+j];
y=w*a[k+j+i/2];
a[k+j]=x+y;
a[k+j+i/2]=x-y;
w=w*wn;
}
}
}
if(flag==-1)for(int i=0;i<N;i++)a[i].r/=N;
}
double anss[maxn];
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++)scanf("%lf",&p[i]);
for(L=0,N=1;N<n;N<<=1,L++);L++;N<<=1;
for(int i=0;i<N;i++){
int len=0;
for(int t=i;t;t>>=1)dig[len++]=t&1;
for(int j=0;j<L;j++)rev[i]=rev[i]*2+dig[j];
}
for(int i=0;i<n;i++)a[i]=cp(p[i],0);
for(int i=1;i<n;i++)b[i]=cp(1.0/i/i,0);
FFT(a,1);FFT(b,1);
for(int i=0;i<N;i++)c[i]=a[i]*b[i];
FFT(c,-1);
for(int i=0;i<n;i++)anss[i]=c[i].r;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
for(int i=0;i<n;i++)a[i]=cp(p[n-i-1],0);
for(int i=1;i<n;i++)b[i]=cp(1.0/i/i,0);
FFT(a,1);FFT(b,1);
for(int i=0;i<N;i++)c[i]=a[i]*b[i];
FFT(c,-1);
for(int i=0;i<n;i++)anss[i]-=c[n-i-1].r;
for(int i=0;i<n;i++)
printf("%.9f\n",anss[i]);
return 0;
}重新过了一遍高精乘
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e6+10;
struct cp{
double r,i;
cp(double _r=0,double _i=0):
r(_r),i(_i){}
cp operator+(cp x){return cp(r+x.r,i+x.i);}
cp operator-(cp x){return cp(r-x.r,i-x.i);}
cp operator*(cp x){return cp(r*x.r-i*x.i,r*x.i+i*x.r);}
};
cp a[maxn],b[maxn],A[maxn],x,y,c[maxn];
char s1[maxn],s2[maxn];
int sum[maxn],a1[maxn],a2[maxn],dig[maxn];
int len1,len2,rev[maxn],N,L;
void FFT(cp a[],int flag){
for(int i=0;i<N;i++)A[i]=a[rev[i]];
for(int i=0;i<N;i++)a[i]=A[i];
for(int i=2;i<=N;i<<=1){
cp wn(cos(2*M_PI/i),flag*sin(2*M_PI/i));
for(int k=0;k<N;k+=i){
cp w(1,0);
for(int j=k;j<k+i/2;j++){
x=a[j];
y=a[j+i/2]*w;
a[j]=x+y;
a[j+i/2]=x-y;
w=w*wn;
}
}
}
if(flag==-1)for(int i=0;i<N;i++)a[i].r/=N;
}
int main(){
scanf("%s%s",s1,s2);
len1=strlen(s1);
len2=strlen(s2);
for(N=1,L=0;N<max(len1,len2);N<<=1,L++);N<<=1;L++;
for(int i=0;i<N;i++){
int len=0;
for(int t=i;t;t>>=1)dig[len++]=t&1;
for(int j=0;j<L;j++)rev[i]=(rev[i]<<1)|dig[j];
}
for(int i=0;i<len1;i++)a1[len1-i-1]=s1[i]-'0';
for(int i=0;i<len2;i++)a2[len2-i-1]=s2[i]-'0';
for(int i=0;i<N;i++)a[i]=cp(a1[i]);
for(int i=0;i<N;i++)b[i]=cp(a2[i]);
FFT(a,1);FFT(b,1);
for(int i=0;i<N;i++)c[i]=a[i]*b[i];
FFT(c,-1);
for(int i=0;i<N;i++)sum[i]=c[i].r+0.5;
for(int i=0;i<N;i++){
sum[i+1]+=sum[i]/10;
sum[i]%=10;
}
int l=len1+len2-1;
while(sum[l]==0&&l>0)l--;
for(int i=l;i>=0;i--)
putchar(sum[i]+'0');
putchar('\n');
return 0;
}









 本文详细介绍了快速傅里叶变换(FFT)的基本概念、原理及其应用。从多项式的不同表达方式出发,逐步深入到复数根的概念,并通过具体的算法实现展示了如何利用FFT进行高效计算。
本文详细介绍了快速傅里叶变换(FFT)的基本概念、原理及其应用。从多项式的不同表达方式出发,逐步深入到复数根的概念,并通过具体的算法实现展示了如何利用FFT进行高效计算。
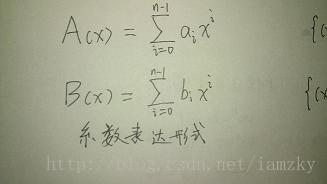


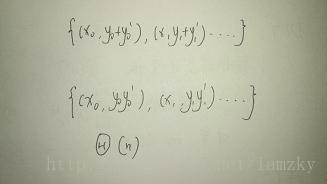



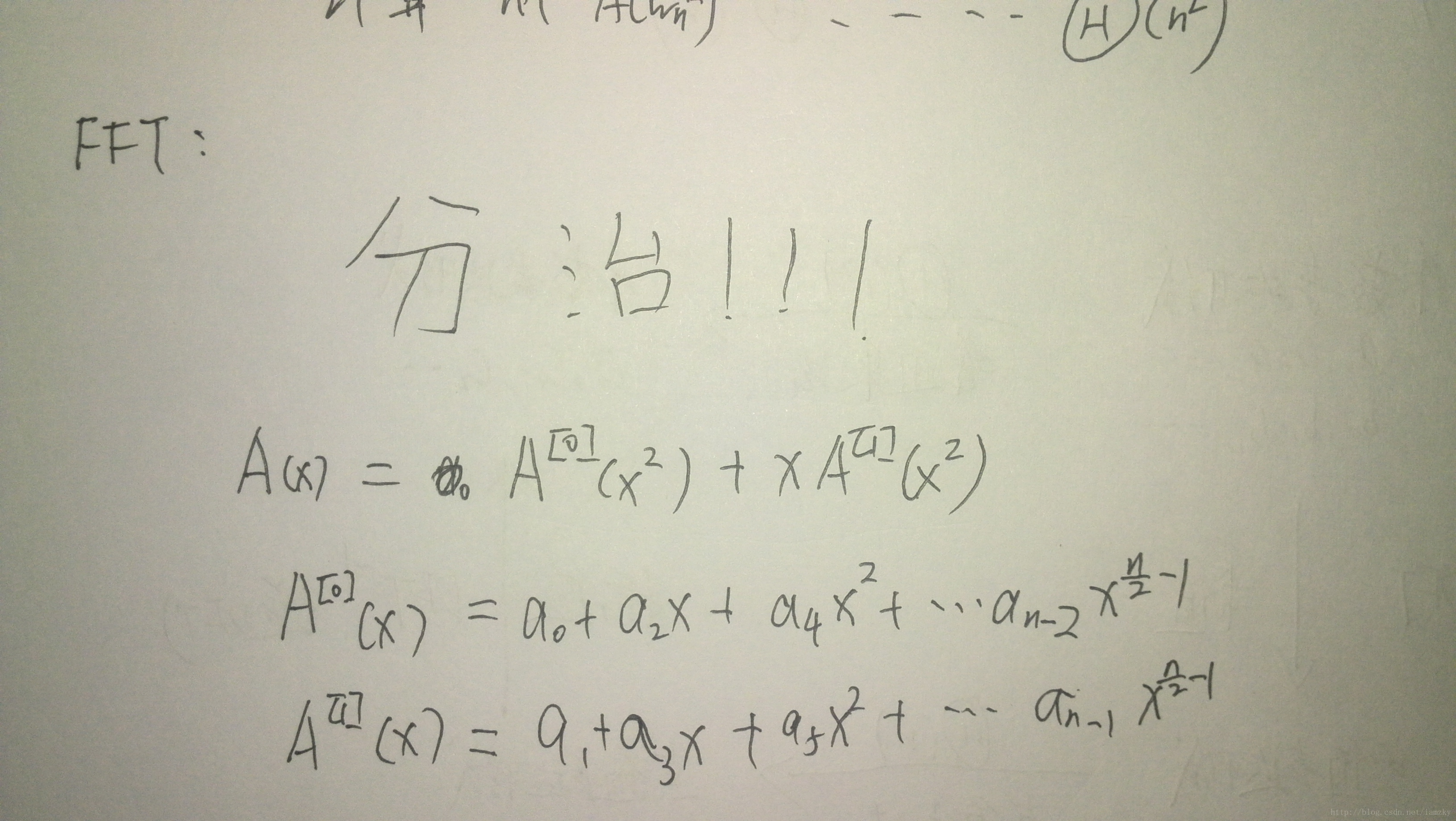


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








