
题目

解决代码及点评
/*
最大对称字符串:在一个字符串里寻找最大长度的对称字符串
对称字符串是指如“abcba” 或者 "abccba"此类的字符串
解决办法:
直接遍历字符串即可
*/
#include<iostream>
using namespace std;
// 获得pos位置上的对称字符串长度
int symstr(char* str, int n, int pos)
{
int calcMax1 = 0;
int calcMax2 = 0;
// 如果str[pos] == str[pos+1]那么是"abba"类型的对称字符串
if (str[pos] == str[pos + 1])
{
calcMax1 = 2;
for (int i = pos; i >= 0; --i)
{
if (pos + pos - i + 2 >= n)
break;
if (str[i - 1] == str[pos + (pos - i) + 2])
{
calcMax1 += 2;
}
}
}
// 如果str[pos-1] == str[pos+1]那么是aba型的对称字符串
if (pos > 0 && str[pos-1] == str[pos+1])
{
calcMax2 = 1;
for (int i = pos; i >= 0; --i)
{
if (pos + pos - i + 1 >= n)
break;
if (str[i - 1] == str[pos + (pos - i) + 1])
{
calcMax2 += 2;
}
}
}
// 根据以上两种类型不同,计算长度,返回较长的类型
return calcMax1 > calcMax2 ? calcMax1 : calcMax2;
}
// 计算最大字符串函数
int maxsymstr(char* str, int n)
{
int maxLen = 0;
int curMax;
// 只是简单的遍历所有字符,然后分别计算最大长度
for (int i = 0; i < n && maxLen / 2 < n-i; i++)
{
// 参数str表示整个字符串,参数n是字符串长度,i是指在该位置计算最大长度
curMax = symstr(str, n, i);
// 如果计算出来的长度比上一次长度还大,则进行保存
if (curMax > maxLen)
maxLen = curMax;
}
return maxLen;
}
int main()
{
// 输入字符串
char str[20];
cin >> str;
// 去计算最大对称字符串
cout << maxsymstr(str, strlen(str)) << endl;
system("pause");
return 0;
}
代码下载及其运行
代码下载地址:http://download.csdn.net/detail/yincheng01/6704519
解压密码:c.itcast.cn
下载代码并解压后,用VC2013打开interview.sln,并设置对应的启动项目后,点击运行即可,具体步骤如下:
1)设置启动项目:右键点击解决方案,在弹出菜单中选择“设置启动项目”
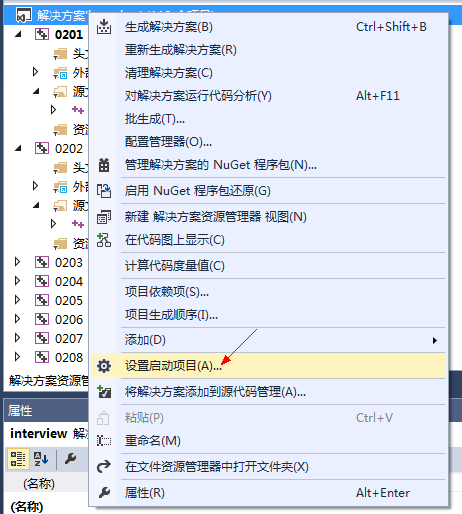
2)在下拉框中选择相应项目,项目名和博客编号一致
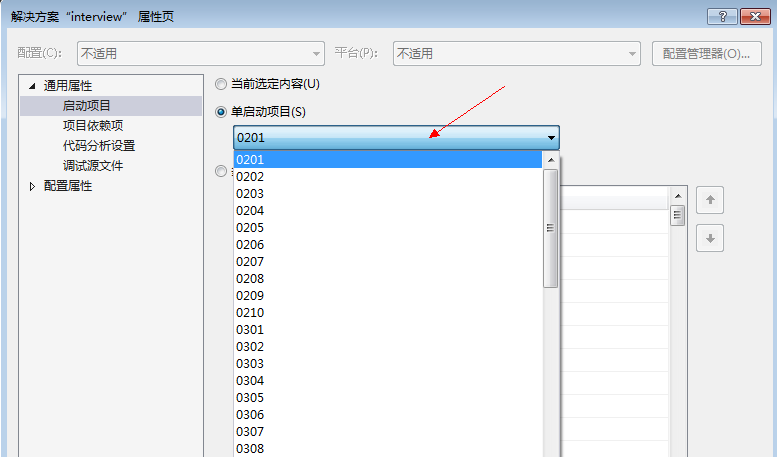
3)点击“本地Windows调试器”运行
程序运行结果








 本文介绍了一种用于查找字符串中最长对称子串的算法实现。通过两种情况的遍历,即“abba”型和“aba”型对称字符串,算法能够找到最长的对称子串并返回其长度。
本文介绍了一种用于查找字符串中最长对称子串的算法实现。通过两种情况的遍历,即“abba”型和“aba”型对称字符串,算法能够找到最长的对称子串并返回其长度。

















 4367
4367

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










