

题目

解决代码及点评
/* 把求子集运算转换为组合问题。 假设集合中包含 N 个元素, 子集合数 = C(N, 0) + C(N, 1) + ... + C(N, N-1) + C(N, N),对于 任一个子集合,可以用一个 N 元组表示,即 <S1, S2, ... Sn-1, Sn>, 其中 Si 取值范围为(0, 1), 0 表示不该子集合不包含该元素,1 表示该子集合包含该元素。因此,求子集合就转换成了 罗列所示可能组合的算法。子集合数 = 2^n。 */ #include <iostream> using namespace std; void Sub(int i, int n, char *pszBuf1, char *pszBuf2) { int j; if (i >= n) { cout<<"("; for (j = 0; j < n; j++) { if (pszBuf2[j] == '1') { cout<<pszBuf1[j]; } } cout<<")"<<endl; } else { pszBuf2[i] = '1'; Sub(i+1, n, pszBuf1, pszBuf2); pszBuf2[i] = '0'; Sub(i+1, n, pszBuf1, pszBuf2); } } int main() { char szBuf1[] = "ac"; char szBuf2[10] = {0}; Sub(0,strlen(szBuf1),szBuf1, szBuf2); system("pause"); return 0; }
代码下载及其运行
代码下载地址:http://download.csdn.net/detail/yincheng01/6704519
解压密码:c.itcast.cn
下载代码并解压后,用VC2013打开interview.sln,并设置对应的启动项目后,点击运行即可,具体步骤如下:
1)设置启动项目:右键点击解决方案,在弹出菜单中选择“设置启动项目”
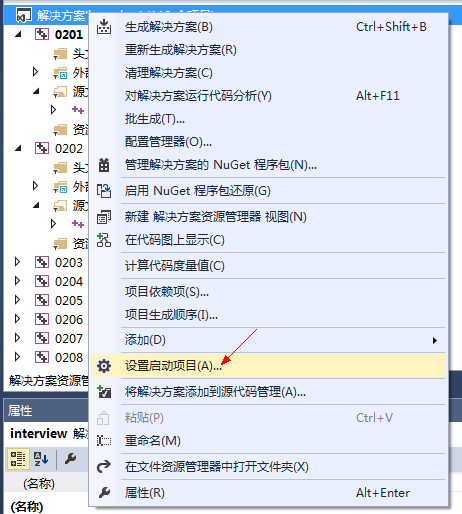
2)在下拉框中选择相应项目,项目名和博客编号一致

3)点击“本地Windows调试器”运行

程序运行结果









 本文介绍了一种通过组合问题转换来生成集合所有子集的算法。使用N元组表示子集,其中每个元素取0或1,代表是否包含原始集合中的对应元素。提供了完整的C++实现代码,展示了如何枚举所有可能的子集。
本文介绍了一种通过组合问题转换来生成集合所有子集的算法。使用N元组表示子集,其中每个元素取0或1,代表是否包含原始集合中的对应元素。提供了完整的C++实现代码,展示了如何枚举所有可能的子集。

















 847
847

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










